2016-2017学年江西省萍乡市芦溪县九年级上学期期中数学试卷
试卷更新日期:2017-04-13 类型:期中考试
一、选择题
-
1. 已知一元二次方程x2﹣x=0,它的解是( )A、0 B、1 C、0,﹣1 D、0,12. 若关于x的方程(m﹣2)x2﹣2x+1=0有两个不等的实根,则m的取值范围是( )A、m<3 B、m≤3 C、m<3且m≠2 D、m≤3且m≠23. 已知 = ,则 的值是( ).A、 B、 C、 D、4. 某小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如图的折线统计图,则符合这一结果的实验最有可能的是( )
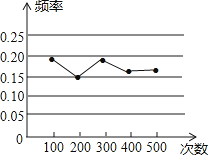 A、在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀” B、一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃 C、暗箱中有1个红球和2个黄球,它们只有颜色上的区别,从中任取一球是黄球 D、掷一个质地均匀的正六面体骰子,向上的面点数是45. 如图,小正方形的边长均为1,则图中三角形(阴影部分)与△ABC相似的是( )
A、在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀” B、一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃 C、暗箱中有1个红球和2个黄球,它们只有颜色上的区别,从中任取一球是黄球 D、掷一个质地均匀的正六面体骰子,向上的面点数是45. 如图,小正方形的边长均为1,则图中三角形(阴影部分)与△ABC相似的是( ) A、
A、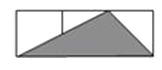 B、
B、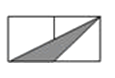 C、
C、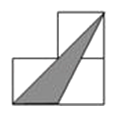 D、
D、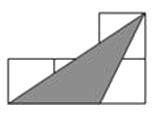 6. 如图,已知矩形ABCD,AB=6,BC=8,E,F分别是AB,BC的中点,AF与DE相交于I,与BD相交于H,则四边形BEIH的面积为( )
6. 如图,已知矩形ABCD,AB=6,BC=8,E,F分别是AB,BC的中点,AF与DE相交于I,与BD相交于H,则四边形BEIH的面积为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
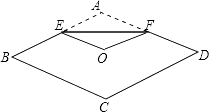
7. 已知一元二次方程x2﹣x﹣c=0有一个根为2,则常数c的值是 .8. 小强和小华两人玩“剪刀、石头、布”游戏,随机出手一次,则两人平局的概率为 .9. Rt△ABC中,∠C=90°,D是AB的中点,若BC=6,AC=8,则CD的长是 .10. 把2米的线段进行黄金分割,则分成的较短线段长为 . (其中黄金比为 )11. 已知一元二次方程:x2﹣3x﹣1=0的两个根分别是x1 , x2 , 则x1x2= .12. 如图,将菱形纸片ABCD折叠,使点A恰好落在菱形的对称中心O处,折痕为EF,若菱形ABCD的边长为2cm,∠A=120°,则EF=cm.
三、解答题
-
13. 解方程:(1)、2x2﹣4x﹣3=0(配方法)(2)、x(x+2)=2+x.14. 如图,在边长为10的正方形ABCD中,△PAQ是正三角形,求PB的长.
 15. 长城公司为希望小学捐赠甲、乙两种品牌的体育器材,甲品牌有A、B、C三种型号,乙品牌有D、E两种型号,现要从甲、乙两种品牌的器材中各选购一种型号进行捐赠.(1)、写出所有的选购方案(用列表法或树状图);(2)、如果在上述选购方案中,每种方案被选中的可能性相同,那么A型器材被选中的概率是多少?16. 已知:如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.
15. 长城公司为希望小学捐赠甲、乙两种品牌的体育器材,甲品牌有A、B、C三种型号,乙品牌有D、E两种型号,现要从甲、乙两种品牌的器材中各选购一种型号进行捐赠.(1)、写出所有的选购方案(用列表法或树状图);(2)、如果在上述选购方案中,每种方案被选中的可能性相同,那么A型器材被选中的概率是多少?16. 已知:如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.求证:四边形BCFE是菱形.
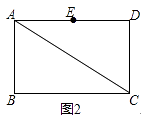
 17. 如图,在矩形ABCD中,点E为AD的中点,请只用无刻度的直尺作图(1)、
17. 如图,在矩形ABCD中,点E为AD的中点,请只用无刻度的直尺作图(1)、如图1,在BC上找点F,使点F是BC的中点;
 (2)、
(2)、如图2,在AC上取两点P,Q,使P,Q是AC的三等分点.
 18. 田忌赛马的故事为我们熟知.小亮与小齐学习概率初步知识后设计了如下游戏:小亮手中有方块10、8、6三张扑克牌,小齐手中有方块9、7、5三张扑克牌.每人从各自手中取出一张牌进行比较,数字大的为本“局”获胜,每次取得牌不能放回.(1)、若每人随机取手中的一张牌进行比赛,求小齐本“局”获胜的概率;(2)、若比赛采用三局两胜制,即胜2局或3局者为本次比赛获胜者.当小亮的三张牌出牌顺序为先出6,再出8,最后出10时,小齐随机出牌应对,求小齐本次比赛获胜的概率.19. 如图,在Rt△ABC中,∠ACB=90°,CD是边AB上的高.
18. 田忌赛马的故事为我们熟知.小亮与小齐学习概率初步知识后设计了如下游戏:小亮手中有方块10、8、6三张扑克牌,小齐手中有方块9、7、5三张扑克牌.每人从各自手中取出一张牌进行比较,数字大的为本“局”获胜,每次取得牌不能放回.(1)、若每人随机取手中的一张牌进行比赛,求小齐本“局”获胜的概率;(2)、若比赛采用三局两胜制,即胜2局或3局者为本次比赛获胜者.当小亮的三张牌出牌顺序为先出6,再出8,最后出10时,小齐随机出牌应对,求小齐本次比赛获胜的概率.19. 如图,在Rt△ABC中,∠ACB=90°,CD是边AB上的高.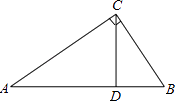 (1)、求证:△ABC∽△CBD;(2)、如果AC=4,BC=3,求BD的长.20. 某商品现在的售价为每件60元,每星期可卖出300件.市场调查反映:每降价1元,每星期可多卖出20件.已知商品的进价为每件40元,在顾客得实惠的前提下,商家还想获得6080元的利润,应将销售单价定为多少元?21. 如图,菱形ABCD的对角线AC,BD相交于点O,过点D作DE∥AC且DE=OC,连接CE,OE.
(1)、求证:△ABC∽△CBD;(2)、如果AC=4,BC=3,求BD的长.20. 某商品现在的售价为每件60元,每星期可卖出300件.市场调查反映:每降价1元,每星期可多卖出20件.已知商品的进价为每件40元,在顾客得实惠的前提下,商家还想获得6080元的利润,应将销售单价定为多少元?21. 如图,菱形ABCD的对角线AC,BD相交于点O,过点D作DE∥AC且DE=OC,连接CE,OE. (1)、求证:OE=CD;(2)、若菱形ABCD的边长为4,∠ABC=60°,求AE的长.22. 如图1,在正方形ABCD内作∠EAF=45°,AE交BC于点E,AF交CD于点F,连接EF,过点A作AH⊥EF,垂足为H.
(1)、求证:OE=CD;(2)、若菱形ABCD的边长为4,∠ABC=60°,求AE的长.22. 如图1,在正方形ABCD内作∠EAF=45°,AE交BC于点E,AF交CD于点F,连接EF,过点A作AH⊥EF,垂足为H.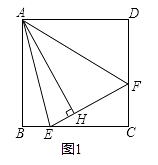 (1)、如图2,将△ADF绕点A顺时针旋转90°得到△ABG.求证:△AGE≌△AFE;
(1)、如图2,将△ADF绕点A顺时针旋转90°得到△ABG.求证:△AGE≌△AFE; (2)、如图3,连接BD交AE于点M,交AF于点N.请探究并猜想:线段BM,MN,ND之间有什么数量关系?并说明理由.
(2)、如图3,连接BD交AE于点M,交AF于点N.请探究并猜想:线段BM,MN,ND之间有什么数量关系?并说明理由. 23. 如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D.点P从点D出发,沿线段DC向点C运动,点Q从点C出发,沿线段CA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到C时,两点都停止.设运动时间为t秒.
23. 如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D.点P从点D出发,沿线段DC向点C运动,点Q从点C出发,沿线段CA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到C时,两点都停止.设运动时间为t秒. (1)、求线段CD的长;(2)、当t为何值时,△CPQ与△ABC相似?(3)、当t为何值时,△CPQ为等腰三角形?
(1)、求线段CD的长;(2)、当t为何值时,△CPQ与△ABC相似?(3)、当t为何值时,△CPQ为等腰三角形?