2016-2017学年江西省景德镇市昌江区九年级上学期期中数学试卷

试卷更新日期：2017-04-13 类型：期中考试

进入 出卷网 下载

一、选择题

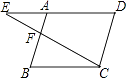
  • 1. 下列命题是假命题的是（   ）
    A、四个角相等的四边形是矩形 B、对角线相等的平行四边形是矩形 C、对角线垂直的四边形是菱形 D、对角线垂直的平行四边形是菱形

    查看试题解析

  • 2. 某种品牌运动服经过两次降价，每件零售价由560元降为315元，已知两次降价的百分率相同，求每次降价的百分率．设每次降价的百分率为x，下面所列的方程中正确的是（   ）

    A、560（1+x）2=315 B、560（1﹣x）2=315 C、560（1﹣2x）2=315 D、560（1﹣x2）=315

    查看试题解析

  • 3. 如图，点F在平行四边形ABCD的边AB上，射线CF交DA的延长线于点E，在不添加辅助线的情况下，与△AEF相似的三角形有（   ）

    A、0个 B、1个 C、2个 D、3个

    查看试题解析

  • 4. 已知实数a、b满足（a2+b2）2﹣2（a2+b2）=8，则a2+b2的值为（　　）


    A、﹣2 B、4 C、4或﹣2 D、﹣4或2

    查看试题解析

  • 5. 如图，在矩形ABCD中，AB=2，BC=3，M为BC中点，连接AM，过D作DE⊥AM于E，则DE的长度为（   ）

    A、2 B、125 C、13 D、5

    查看试题解析

二、填空题

  • 6. 已知关于x的方程（m2﹣1）x2+（m+1）x+m﹣2=0，当m时，方程为一元二次方程．

    查看试题解析

  • 7. 已知在△ABC中，AD⊥BC，垂足为点D，DE∥AC交AB于E，DF∥AB交AC于F，当△ABC再添加一个条件：时，四边形AEDF为菱形（填写一个条件即可）．

    查看试题解析

  • 8. 设x1、x2是方程x2﹣4x+m=0的两个根，且x1+x2﹣x1x2=1．则m= ．

    查看试题解析

  • 9. 如图，在▱ABCD中，点E是边AD的中点，EC交对角线BD于点F，则 S△DEFS△BCF = ．

    查看试题解析

  • 10. 如图，已知正方形ABCD的对角线长为2 2 ，将正方形ABCD沿直线EF折叠，则图中阴影部分的周长为 ．

    查看试题解析

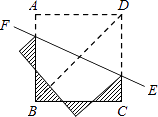  • 11. 如图，矩形ABCD中，AB=6，BC=8，点E是BC边上一点，连接AE，把∠B沿AE折叠，使点B落在点B′处，当△CEB′为直角三角形时，BE的长为 ．

    查看试题解析

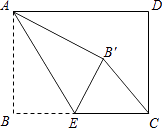  • 12. 综合题。
    (1)、解方程：2（x﹣3）2=x2﹣9
    (2)、已知 a2=b3 ≠0，求代数式 5a−2ba+2b 的值．

    查看试题解析

  • 13. 试证明：不论m为何值，方程2x2﹣（4m﹣1）x﹣m2﹣m=0总有两个不相等的实数根．

    查看试题解析

  • 14. 如图，AB=AC，AD=AE，DE=BC，且∠BAD=∠CAE．

    求证：四边形BCDE是矩形．

    查看试题解析

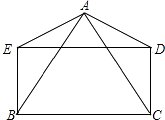  • 15. 如图，两张宽为1cm的矩形纸条交叉叠放，其中重叠部分部分是四边形ABCD，

    (1)、试判断四边形ABCD的形状，并说明理由
    (2)、若∠BAD=30°，求重叠部分的面积．

    查看试题解析

  • 16. 如图，在△ABC中，AD是角平分钱，点E在AC上，且∠EAD=∠ADE．

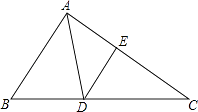    (1)、求证：△DCE∽△BCA；
    (2)、若AB=3，AC=4．求DE的长．

    查看试题解析

  • 17. 已知关于x的一元二次方程x2﹣4x+k+1=0
    (1)、若x=﹣1是方程的一个根，求k值和方程的另一根；
    (2)、设x1 ， x2是关于x的方程x2﹣4x+k+1=0的两个实数根，是否存在实数k，使得x1x2＞x1+x2成立？请说明理由．

    查看试题解析

  • 18. 如图所示，长方形ABCD是“阳光小区”内一块空地，已知AB=2a，BC=3b，且E为AB边的中点，CF= 13 BC，现打算在阴影部分种植一片草坪，求这片草坪的面积．

    查看试题解析

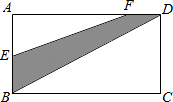  • 19. 如果两个一次函数y=k1x+b1和y=k2x+b2满足k1=k2 ， b1≠b2 ， 那么称这两个一次函数为“平行一次函数”．

    如图，已知函数y=﹣2x+4的图象与x轴、y轴分别交于A、B两点，一次函数y=kx+b与y=﹣2x+4是“平行一次函数”

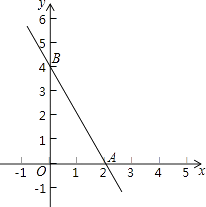    (1)、若函数y=kx+b的图象过点（3，1），求b的值；
    (2)、若函数y=kx+b的图象与两坐标轴围成的三角形和△AOB构成位似图形，位似中心为原点，位似比为1：2，求函数y=kx+b的表达式．

    查看试题解析

  • 20. 如图，菱形EFGH的三个顶点E、G、H分别在正方形ABCD的边AB、CD、DA上，连接CF．

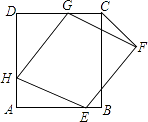    (1)、求证：∠HEA=∠CGF；
    (2)、当AH=DG时，求证：菱形EFGH为正方形．

    查看试题解析

  • 21. 某商店销售甲、乙两种商品，现有如下信息：

    请结合以上信息，解答下列问题：

    (1)、求甲、乙两种商品的进货单价；
    (2)、已知甲、乙两种商品的零售单价分别为2元、3元，该商店平均每天卖出甲商品500件和乙商品1300件，经市场调查发现，甲种商品零售单价每降0.1元，甲种商品每天可多销售100件，商店决定把甲种商品的零售单价下降m（m＞0）元，在不考虑其他因素的条件下，求当m为何值时，商店每天销售甲、乙两种商品获取的总利润为1800元（注：单件利润=零售单价﹣进货单价）

    查看试题解析

  • 22. 如图1，点P在正方形ABCD的对角线AC上，正方形的边长是a，Rt△PEF的两条直角边PE、PF分别交BC、DC于点M、N．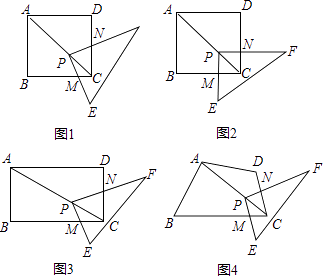

    (1)、操作发现：如图2，固定点P，使△PEF绕点P旋转，当PM⊥BC时，四边形PMCN是正方形．填空：①当AP=2PC时，四边形PMCN的边长是；②当AP=nPC时（n是正实数），四边形PMCN的面积是 ．
    (2)、猜想论证

    如图3，改变四边形ABCD的形状为矩形，AB=a，BC=b，点P在矩形ABCD的对角线AC上，Rt△PEF的两条直角边PE、PF分别交BC、DC于点M、N，固定点P，使△PEF绕点P旋转，则 PMPN  = ．

    (3)、拓展探究

    如图4，当四边形ABCD满足条件：∠B+∠D=180°，∠EPF=∠BAD时，点P在AC上，PE、PF分别交BC，CD于M、N点，固定P点，使△PEF绕点P旋转，请探究 PMPN 的值，并说明理由．

    查看试题解析