2016-2017学年江西省抚州市崇仁县九年级上学期期中数学试卷
试卷更新日期：2017-04-13 类型：期中考试
一、选择题：
-
1. 用配方法解方程x2﹣2x﹣6=0时，原方程应变形为（ ）A、（x+1）2=7 B、（x﹣1）2=7 C、（x+2）2=10 D、（x﹣2）2=102. 方程2x2﹣kx﹣1=0的根的情况是（ ）A、方程有两个相等的实数根 B、方程有两个不相等的实数根 C、方程没有实数根 D、方程的根的情况与k的取值有关3. 某旅游景点三月份共接待游客25万人次，五月份共接待游客64万人次，设每月的平均增长率为x，则可列方程为（ ）A、25（1+x）2=64 B、25+25（1+x）2=64 C、25（1+2x）=64 D、64（1﹣x2）=254. 一个不透明的口袋里装有除颜色外都相同的5个白球和若干个红球，在不允许将球倒出来数的前提下，小亮为了估计其中的红球数，采用如下方法：先将口袋中的球摇匀，再从口袋里随机摸出一球，记下颜色，然后把它放回口袋中，不断重复上述过程，小亮共摸了100次，其中有10次摸到白球．因此小亮估计口袋中的红球大约有（ ）个．A、45 B、48 C、50 D、555. 如图，以点O为位似中心，将△ABC放大得到△DEF.若AD=OA ， 则△ABC与△DEF的面积之比为（ ）
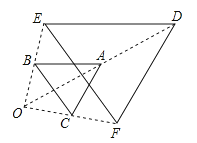A、1：2 B、1：4 C、1：5 D、1：66. 如图，点A，B，C，D的坐标分别是（1，7），（1，1），（4，1），（6，1），以C，D，E为顶点的三角形与△ABC相似，则点E的坐标不可能是（ ）
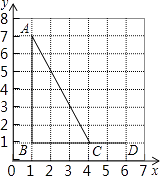A、（6，0） B、（6，3） C、（6，5） D、（4，2）二、填空题：
-
7. 方程x（x+3）=0的解是 ．8. 如图，在△ABC中，点D，E分别在边AB，AC上，DE∥BC，已知AE=6， ，则EC的长是 ．
9. 在1×2的正方形网格格点上放三枚棋子，按图所示的位置已放置了两枚棋子，若第三枚棋子随机放在其它格点上，则以这三枚棋子所在的格点为顶点的三角形是直角三角形的概率是 ．
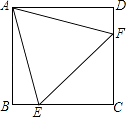
10. 如图，身高为1.6米的学生想测量学校旗杆的高度，当他站在C处时，他头顶端的影子正好与旗杆顶端的影子重合，并测得AC=2米，BC=8米，则旗杆的高度是米．
11. 如图，在正方形ABCD中，边长为2的等边三角形AEF的顶点E、F分别在BC和CD上，下列结论：①CE=CF；②∠AEB=75°；③BE+DF=EF；④S正方形ABCD=2+ ．
其中正确的序号是（把你认为正确的都填上）．
三、解答题：
-
12. 解方程：
①4x（2x+1）=3（2x+1）
②（x+3）（x﹣1）=5．
13. 已知，如图，以矩形ABCD的一边CD为边向外作等边△PCD，请你用无刻度的直尺作出线段AB的垂直平分线（保留作图痕迹）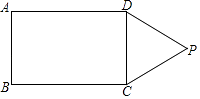
14. 已知：▱ABCD的两边AB，AD的长是关于x的方程x2﹣mx+ ﹣ 的两个实数根．(1)、当m为何值时，▱ABCD是菱形？(2)、若AB的长为2，那么▱ABCD的周长是多少？15. 如图，M是矩形ABCD的边AD的中点，P为BC上一点，PE⊥MC，PF⊥MB，垂足分别为E，F，当AB，BC满足什么条件时，四边形PEMF为矩形？试加以证明．
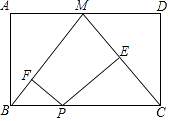16. 在正方形ABCD中，P是BC上一点，且BP=3PC，Q是CD得中点．
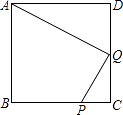(1)、证明△ADQ∽△QCP；(2)、求证：AQ⊥QP．17. 甲、乙、丙三人之间相互传球，球从一个人手中随机传到另外一个人手中，共传球三次．(1)、若开始时球在甲手中，求经过三次传球后，球传回到甲手中的概率是多少？(2)、若乙想使球经过三次传递后，球落在自己手中的概率最大，乙会让球开始时在谁手中？请说明理由．18. 某公司投资新建了一商场，共有商铺30间．据预测，当每间的年租金定为10万元时，可全部租出．每间的年租金每增加5000元，少租出商铺1间．该公司要为租出的商铺每间每年交各种费用1万元，未租出的商铺每间每年交各种费用5000元．(1)、当每间商铺的年租金定为13万元时，能租出多少间？(2)、当每间商铺的年租金定为多少万元时，该公司的年收益（收益=租金﹣各种费用）为275万元？19. 如图，在矩形ABCD中，AB=4cm，BC=8cm，AC的垂直平分线EF分别交AD，BC于点E，F，垂足为点O．
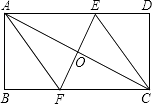(1)、连接AF，CE，求证：四边形AFCE为菱形；(2)、求AF的长．20. 将一副三角尺如图①摆放（在Rt△ABC中，∠ACB=90°，∠B=60°；在Rt△DEF中，∠EDF=90°，∠E=45°）．点D为AB的中点，DE交AC于点P，DF经过点C．
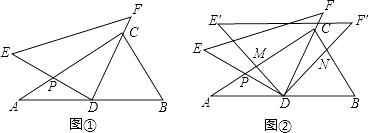(1)、求∠ADE的度数；(2)、如图②，在图①的基础上将△DEF绕点D顺时针方向旋转角α（0°＜α＜60°），此时的等腰直角三角尺记为△DE′F′，DE′交AC于点M，DF′交BC于点N，求证： ．21. 如图①，在正方形ABCD中，P是对角线AC上的一点，点E在BC的延长线上，且PE=PB．
(1)、求证：△BCP≌△DCP；(2)、求证：∠DPE=∠ABC；(3)、把正方形ABCD改为菱形，其它条件不变（如图②），若∠ABC=58°，则∠DPE=度．22. 如图，在平面直角坐标系内，已知点A（0，6）、点B（8，0），动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O移动，同时动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A移动，设点P、Q移动的时间为t秒．
(1)、求直线AB的解析式；(2)、当t为何值时，△APQ与△AOB相似？(3)、当t为何值时，△APQ的面积为 个平方单位？