2016-2017学年吉林省长春市朝阳区九年级上学期期中数学试卷
试卷更新日期:2017-04-12 类型:期中考试
一、选择题
-
1. 下列各式中,是最简二次根式的是( )A、 B、 C、 D、2. 一元二次方程x2﹣16=0的根是( )A、x=2 B、x=4 C、x1=2,x2=﹣2 D、x1=4,x2=﹣43. 如图,AD∥BE∥CF,直线l1 , l2与这三条平行线分别交于A,B,C和点D,E,F.若AB=2,BC=4,DE=3,则EF的长为( )
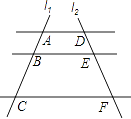 A、5 B、6 C、7 D、94. 一元二次方程x2﹣4x+1=0的根的情况是( )A、没有实数根 B、只有一个实数根 C、有两个相等的实数根 D、有两个不相等的实数根5. 下列运算中正确的是( )A、 ﹣ = B、2 +3 =6 C、 = D、( +1)( ﹣1)=36. 一个正方形的面积是12,它的边长在两个相邻整数之间,则这两个整数是( )A、1和2 B、2和3 C、3和4 D、4和57. 某超市一月份的营业额为36万元,三月份的营业额为48万元,设每月的平均增长率为x,则可列方程为( )A、48(1﹣x)2=36 B、48(1+x)2=36 C、36(1﹣x)2=48 D、36(1+x)2=488. 如图,△ABC中,∠A=78°,AB=4,AC=6.将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不一定相似的是( )
A、5 B、6 C、7 D、94. 一元二次方程x2﹣4x+1=0的根的情况是( )A、没有实数根 B、只有一个实数根 C、有两个相等的实数根 D、有两个不相等的实数根5. 下列运算中正确的是( )A、 ﹣ = B、2 +3 =6 C、 = D、( +1)( ﹣1)=36. 一个正方形的面积是12,它的边长在两个相邻整数之间,则这两个整数是( )A、1和2 B、2和3 C、3和4 D、4和57. 某超市一月份的营业额为36万元,三月份的营业额为48万元,设每月的平均增长率为x,则可列方程为( )A、48(1﹣x)2=36 B、48(1+x)2=36 C、36(1﹣x)2=48 D、36(1+x)2=488. 如图,△ABC中,∠A=78°,AB=4,AC=6.将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不一定相似的是( ) A、
A、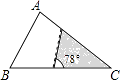 B、
B、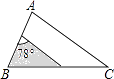 C、
C、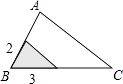 D、
D、
二、填空题
-
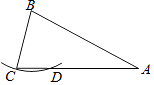
9. 若 在实数范围内有意义,则x的取值范围是 .10. 用配方法解方程x2﹣8x=3时,方程的两边同时加上一个实数 , 使得方程左边配成一个完全平方式.11. = .12. 若a是方程x2﹣5x﹣4=0的根,则a2﹣5a的值为 .13. 如图,在△ABC中,AB=AC=2BC,以点B为圆心,BC长为半径作弧,与AC交于点D.若AC=4,则线段CD的长为 .
 14. 如图,在边长为3的菱形ABCD中,点E在边CD上,点F为BE延长线与AD延长线的交点.若DE=1,则DF的长为 .
14. 如图,在边长为3的菱形ABCD中,点E在边CD上,点F为BE延长线与AD延长线的交点.若DE=1,则DF的长为 .
三、解答题
-
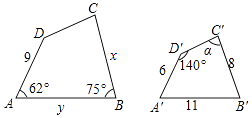
15. 计算: (2﹣ )+2 .16. 解方程:2x2+x﹣4=0.17. 如图,四边形ABCD∽四边形A′B′C′D′,求边x、y的长度和角α的大小.
 18. 已知x=1是一元二次方程(a﹣2)x2+(a2﹣3)x﹣a+1=0的一个根,求a的值.19. 如图,图①、图②、图③均为4×2的正方形网格,△ABC的顶点均在格点上.按要求在图②、图③中各画一个顶点在格点上的三角形.
18. 已知x=1是一元二次方程(a﹣2)x2+(a2﹣3)x﹣a+1=0的一个根,求a的值.19. 如图,图①、图②、图③均为4×2的正方形网格,△ABC的顶点均在格点上.按要求在图②、图③中各画一个顶点在格点上的三角形.要求:

所画的两个三角形都与△ABC相似但都不与△ABC全等.
图②和图③中新画的三角形不全等.
20. 某课外活动小组借助如图所示的直角墙角(两边足够长)用篱笆围成矩形花园ABCD,篱笆只围AB、BC两边,已知篱笆长为30m,篱笆围成的矩形ABCD的面积为225m2 , 求边AB的长. 21. 如图,在矩形ABCD中,已知AD>AB,在边AD上取点E,连结CE,过点E作EF⊥CE,与边AB的延长线交于点F.
21. 如图,在矩形ABCD中,已知AD>AB,在边AD上取点E,连结CE,过点E作EF⊥CE,与边AB的延长线交于点F.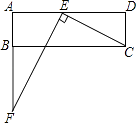 (1)、证明:△AEF∽△DCE.(2)、若AB=2,AE=3,AD=7,求线段AF的长.22. 感知:
(1)、证明:△AEF∽△DCE.(2)、若AB=2,AE=3,AD=7,求线段AF的长.22. 感知: (1)、如图①,在四边形ABCD中,AB∥CD,∠B=90°,点P在BC边上,当∠APD=90°时,可知△ABP∽△PCD.(不要求证明)(2)、探究:如图②,在四边形ABCD中,点P在BC边上,当∠B=∠C=∠APD时,求证:△ABP∽△PCD.(3)、拓展:如图③,在△ABC中,点P是边BC的中点,点D、E分别在边AB、AC上.若∠B=∠C=∠DPE=45°,BC=4 ,CE=3,则DE的长为 .23. 某淘宝网店销售台灯,成本为每个30元.销售大数据分析表明:当每个台灯售价为40元时,平均每月售出600个;若售价每上涨1元,其月销售量就减少20个,若售价每下降1元,其月销售量就增加200个.(1)、若售价上涨x元(x>0),每月能售出 个台灯.
(1)、如图①,在四边形ABCD中,AB∥CD,∠B=90°,点P在BC边上,当∠APD=90°时,可知△ABP∽△PCD.(不要求证明)(2)、探究:如图②,在四边形ABCD中,点P在BC边上,当∠B=∠C=∠APD时,求证:△ABP∽△PCD.(3)、拓展:如图③,在△ABC中,点P是边BC的中点,点D、E分别在边AB、AC上.若∠B=∠C=∠DPE=45°,BC=4 ,CE=3,则DE的长为 .23. 某淘宝网店销售台灯,成本为每个30元.销售大数据分析表明:当每个台灯售价为40元时,平均每月售出600个;若售价每上涨1元,其月销售量就减少20个,若售价每下降1元,其月销售量就增加200个.(1)、若售价上涨x元(x>0),每月能售出 个台灯.
(2)、为迎接“双十一”,该网店决定降价促销,在库存为1210个台灯的情况下,若预计月获利恰好为8400元,求每个台灯的售价.(3)、在库存为1000个台灯的情况下,若预计月获利恰好为8000元,直接写出每个台灯的售价.24. 如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,动点D从点A出发以每秒3个单位的速度运动至点B,过点D作DE⊥AB交射线AC于点E.设点D的运动时间为t秒(t>0).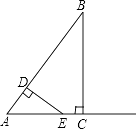 (1)、线段AE的长为 . (用含t的代数式表示)(2)、若△ADE与△ACB的面积比为1:4时,求t的值.(3)、设△ADE与△ACB重叠部分图形的周长为L,求L与t之间的函数关系式.(4)、当直线DE把△ACB分成的两部分图形中有一个是轴对称图形时,直接写出t的值.
(1)、线段AE的长为 . (用含t的代数式表示)(2)、若△ADE与△ACB的面积比为1:4时,求t的值.(3)、设△ADE与△ACB重叠部分图形的周长为L,求L与t之间的函数关系式.(4)、当直线DE把△ACB分成的两部分图形中有一个是轴对称图形时,直接写出t的值.