2016-2017学年湖北省孝感市云梦县九年级上学期期中数学试卷

试卷更新日期：2017-04-12 类型：期中考试

进入出卷网下载

一、选择题

1. 方程4x²﹣3x=1的二次项系数和一次项系数分别为（）

A、4和3 B、4和﹣3 C、4和﹣1 D、4和1

查看试题解析
2. 用配方法解方程x²+6x+4=0，下列变形正确的是（　　）

A、（x+3）²=﹣4 B、（x﹣3）²=4 C、（x+3）²=5 D、（x+3）²=± $\sqrt{5}$

查看试题解析
3. 下列图形中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 关于x的一元二次方程（m﹣1）x²+5x+m²﹣3m+2=0的常数项为0，则m等于（）

A、1 B、2 C、1或2 D、0

查看试题解析
5. 平面直角坐标系内，与点P（﹣3，2）关于原点对称的点的坐标是（）

A、（3，﹣2） B、（2，3） C、（2，﹣3） D、（﹣3，﹣2）

查看试题解析
6. 已知二次函数y=x²﹣2x+m（m为常数）的图象与x轴的一个交点为（﹣1，0），则关于x的一元二次方程x²﹣2x+m=0的两个实数根是（）

A、x₁=1，x₂=2 B、x₁=1，x₂=3 C、x₁=﹣1，x₂=2 D、x₁=﹣1，x₂=3

查看试题解析
7. 等腰三角形一条边的边长为3，它的另两条边的边长是关于x的一元二次方程x²﹣12x+k=0的两个根，则k的值是（）

A、27 B、36 C、27或36 D、18

查看试题解析
8. 二次函数y=﹣2x²的图象如何移动，就得到y=﹣2x²+4x+1的图象（）

A、向左移动1个单位，向上移动3个单位 B、向左移动1个单位，向下移动3个单位 C、向右移动1个单位，向上移动3个单位 D、向右移动1个单位，向下移动3个单位

查看试题解析
9. 如图，⊙O是△ABC的外接圆，∠B=60°，OP⊥AC于点P，OP=2，则⊙O的半径为（）

A、2 $\sqrt{3}$ B、4 C、4 $\sqrt{3}$ D、6

查看试题解析
10. 已知二次函数y=ax²+bx+c的图象与x轴交于（x₁ ， 0），（x₂ ， 0）两点，且0＜x₁＜1，1＜x₂＜2，与y轴交于（0，﹣2）．下列结论：①2a+b＞1； ②a+b＞2；③a﹣b＜2；④3a+b＞0； ⑤a＜﹣1．其中正确结论的个数为（）

A、2 B、3 C、4 D、5

查看试题解析

二、填空题

11. 若关于x的方程（m﹣ $\sqrt{3}$ ）x $^{m^{2} - 1}$ ﹣ $\sqrt{3}$ x+2=0是一元二次方程，则m的值是．

查看试题解析
12. 若抛物线y=2x²+mx+8与x轴只有一个公共点，则m的值为．

查看试题解析
13. 若抛物线y=x²﹣2016x+2017与x轴的两个交点为（m，0）与（n，0），则（m²﹣2017m+2017）（n²﹣2017n+2017）=

查看试题解析
14. 如图是一座抛物形拱桥，当水面的宽为12m时，拱顶离水面4m，当水面下降3m时，水面的宽为 m．

查看试题解析
15. 如图，△ABC内接于⊙O，∠BAC=120°，AB=AC，BD为⊙O的直径，AB=5，则CD= ．

查看试题解析
16.
如图，在平面直角坐标系中，将△ABO绕点A顺时针旋转到△AB₁C₁的位置，点B、O分别落在点B₁、C₁处，点B₁在x轴上，再将△AB₁C₁绕点B₁顺时针旋转到△A₁B₁C₂的位置，点C₂在x轴上，将△A₁B₁C₂绕点C₂顺时针旋转到△A₂B₂C₂的位置，点A₂在x轴上，依次进行下去…．若点A（3，0），B（0，4），则点B₁₀₀的坐标为．

查看试题解析

三、解答题

17. 用适当的方法解下列方程：

(1)、x²+2x﹣9999=0

(2)、2x²﹣2x﹣1=0．

查看试题解析
18.
如图，在平面直角坐标系中，Rt△ABC的三个顶点分别是A（﹣3，2），B（0，4），C（0，2）．

(1)、将△ABC以点C为旋转中心旋转180°，画出旋转后对应的△A₁B₁C；平移△ABC，若点A的对应点A₂的坐标为（0，﹣4），画出平移后对应的△A₂B₂C₂；

(2)、若将△A₁B₁C绕某一点旋转可以得到△A₂B₂C₂；请直接写出旋转中心的坐标；

(3)、在x轴上有一点P，使得PA+PB的值最小，请直接写出点P的坐标．

查看试题解析
19. 已知关于x的一元二次方程（a+c）x²+2bx+（a﹣c）=0，其中a、b、c分别为△ABC三边的长．

(1)、如果x=﹣1是方程的根，试判断△ABC的形状，并说明理由；

(2)、如果方程有两个相等的实数根，试判断△ABC的形状，并说明理由；

(3)、如果△ABC是等边三角形，试求这个一元二次方程的根．

查看试题解析
20. 已知关于x的一元二次方程x²﹣2x+m﹣1=0有两个实数根x₁ ， x₂ ．

(1)、求m的取值范围；

(2)、当x₁²+x₂²=6x₁x₂时，求m的值．

查看试题解析
21. ⊙O的半径为17cm，AB，CD是⊙O的两条弦，AB∥CD，AB=30cm，CD=16cm．求AB和CD之间的距离．

查看试题解析
22. 如图，P是正三角形ABC内的一点，且PA=6，PB=8，PC=10，将△APB绕点B逆时针旋转一定角度后，可得到△CQB．

(1)、求点P与点Q之间的距离；

(2)、求∠APB的度数．

查看试题解析
23. 某水果批发商销售每箱进价为40元的苹果，物价部门规定每箱售价不得高于55元，市场调查发现，若每箱以50元的价格出售，平均每天销售90箱，价格每提高1元，平均每天少销售3箱．

(1)、求平均每天销售量y（箱）与销售价x（元/箱）之间的函数关系式．

(2)、求该批发商平均每天的销售利润w（元）与销售价x（元/箱）之间的函数关系式．

(3)、当每箱苹果的销售价为多少元时，可以获得最大利润？最大利润是多少？

查看试题解析
24.
如图，直线y=x+2与抛物线y=ax²+bx+6（a≠0）相交于A（ $\frac{1}{2}$ ， $\frac{5}{2}$ ）和B（4，m），点P是线段AB上异于A、B的动点，过点P作PC⊥x轴于点D，交抛物线于点C．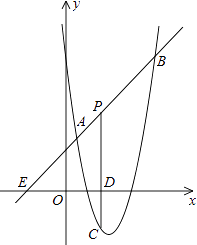

(1)、求抛物线的解析式；

(2)、是否存在这样的P点，使线段PC的长有最大值？若存在，求出这个最大值；若不存在，请说明理由；

(3)、求△PAC为直角三角形时点P的坐标．

查看试题解析