沪科版八年级数学上册 12.1 函数（3）同步练习
试卷更新日期：2019-01-18 类型：同步测试
一、选择题
-
1. 下列图象不能表示函数关系的是（ ）A、
B、
C、
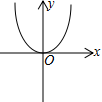D、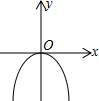
2. 我们学习了一次函数、二次函数和反比例函数，回顾学习过程，都是按照列表、描点、连线得到函数的图象，然后根据函数的图象研究函数的性质，这种研究方法主要体现的数学思想是（ ）A、演绎 B、数形结合 C、抽象 D、公理化3. 一列动车从A地开往B地，一列普通列车从B地开往A地，两车同时出发，设普通列车行驶的时间为x（小时），两车之间的距离为y（千米），如图中的折线表示y与x之间的函数关系．下列叙述错误的是（ ）
A、AB两地相距1000千米 B、两车出发后3小时相遇 C、动车的速度为
D、普通列车行驶t小时后，动车到达终点B地，此时普通列车还需行驶 
千米到达A地
4. 汽车的“燃油效率”是指汽车每消耗1升汽油行驶的最大公里数（单位：km/L），如图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况，下列叙述正确的是（ ）
A、以相同速度行驶相同路程，甲车消耗汽油最多 B、以10km/h的速度行驶时，消耗1升汽油，甲车最少行驶5千米 C、以低于80km/h的速度行驶时，行驶相同路程，丙车消耗汽油最少 D、以高于80km/h的速度行驶时，行驶相同路程，丙车比乙车省油5. 如图，四幅图象分别表示变量之间的关系，请按图象的顺序，将下面的四种情境与之对应排序．正确的顺序是（ ）
a篮球运动员投篮时，投出去的篮球的高度与时间的关系
b去超市购买同一单价的水果，所付费用与水果数量的关系
c李老师使用的是一种含月租的手机计费方式，则他每月所付话费与通话时间的关系
d周末，小明从家到图书馆，看了一段时间书后，按原速度原路返回，小明离家的距离与时间的关系
A、abcd B、acdb C、acbd D、adbc6. 甲、乙两名同学进行登山比赛，甲同学和乙同学沿相同的路线同时在早8：00从山脚出发前往山顶，甲同学到达山顶后休息1小时，沿原路以每小时6千米的速度下山，在这一过程中，各自行进的路程随所用时间变化的图象如图所示，根据提供信息得出以下四个结论：甲同学从山脚到达山顶的路程为12千米； 乙同学登山共用4小时； 甲同学在14：00返回山脚；④甲同学返回与乙同学相遇时，乙同学距登到山顶还有 千米的路程．
以上四个结论正确的有（ ）个
A、1 B、2 C、3 D、47. 如图，在△ABC中，∠B＝90°，AB＝3cm，BC＝6cm，动点P从点A开始沿AB向点B以1cm/s的速度移动，动点Q从点B开始沿BC向点C以2cm/s的速度移动，若P，Q两点分别从A，B两点同时出发，P点到达B点运动停止，则△PBQ的面积S随出发时间t的函数关系图象大致是（ ）
A、
B、
C、
D、
8. 有一个安装有进出水管的30升容器，水管单位时间内进出的水量是一定的，设从某时刻开始的4分钟内只进水不出水，在随后的8分钟内既进水又出水，得到水量y(升)与时间x(分)之间的函数关系如图所示．根据图象信息给出下列说法：
①每分钟进水5升；②当4≤x≤12时，容器中水量在减少；③若12分钟后只放水，不进水，还要8分钟可以把水放完；④若从一开始进出水管同时打开需要24分钟可以将容器灌满．
以上说法中正确的有（ ）A、1个 B、2个 C、3个 D、4个二、填空题
-
9. 张师傅驾车从甲地到乙地匀速行驶，已知行驶中油箱剩余油量y（升）与行驶时间t（小时）之间的关系用如图的线段AB表示，根据这个图象求出y与t之间的函数关系式为y=﹣7.5t+25，那么函数y=﹣7.5t+25中的常数﹣7.5表示的实际意义是 ．
10. 某市出租车收费标准如下：起租费：5元；基价里程：3公里；等时费：每等5分钟加收1公里的租价；租价：每公里1.20元．星期天，某同学从家出发坐出租车去火车站接一朋友回家．如图表示该同学离家距离与离家时间的关系如图所示，则该同学最少应付车费元．（注：1公里=1千米）
11. 园林队在某公司进行绿化，中间休息了一段时间，已知绿化面积S（平方米）与工作时间t（小时）的关系的图像如图所示，则休息后园林队每小时绿化面积为平方米．
12. 如图，OB，AB分别表示甲乙两名同学运动的一次函数图象，图中s与t分别表示运动路程和时间，已知甲的速度比乙快，下列说法：①射线AB表示甲的路程与时间的函数关系；②甲的速度比乙快1.5米/秒；③甲比乙先跑12米；④8秒钟后，甲超过了乙，其中正确的有.（填写你认为所有正确的答案序号）
13. 一个装有进水管和出水管的容器，从某时刻开始4min内只进水不出水，在随后的8min内既进水又出水，接着关闭进水管直到容器内的水放完，每分钟的进水量和出水量是两个常数，容器内的水量y（单位：L)与时间（单价：min）之间的关系如图所示。在第分钟时该容器内的水恰好为10L。
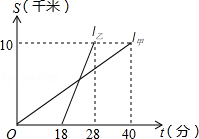
14. 如图①，在矩形MNPQ中，动点R从点N出发，沿N→P→Q→M方向运动至点M处停止，设点R运动的路程为x，△MNR的面积为y，如果y关于x的函数图象如图②所示，则矩形MNPQ的面积是 ．
15. 甲、乙两人以相同路线前往距离单位10km的培训中心参加学习．图中l甲、l乙分别表示甲、乙两人前往目的地所走的路程S（km）随时间t（分）变化的函数图象．以下说法：①乙比甲提前12分钟到达；②甲的平均速度为15千米/小时；③乙走了8km后遇到甲；④乙出发6分钟后追上甲．其中正确的有（填所有正确的序号）．
三、解答题
-
16. 四个容量相等的容器形状如图1所示，用同一流量的水管分别向这四个容器注水，所需时间都相同，如图2所示的是容器水位(h)与时间(t)的关系的图象．
请把适当的图象序号与相应容器形状的字母代号用线段相连接。
17. 光大路桥公司中标承包了一段路基工程，进入施工场地后，所挖路基的长度y（m）与工作时间x（天）之间的函数关系如图所示，请根据提供的信息解答下列问题：
(1)、求y与x的函数关系式；(2)、预测完成1620m的路基工程，需要工作多少天？18. 某厂生产的RGZ-120型体重秤，最大称重120千克，你在体检时可看到如图（1）所示的显示盘。已知指针顺时针旋转角x（度）与体重y（千克）有如下关系：x（度）
0
72
144
216
y（千克）
0
25
50
75
(1)、根据表格中的数据在平面直角坐标系图（2）中描出相应的点，顺次连接各点后，你发现这些点在哪一种函数的图象上？合情猜想符合这个图象的函数解析式；(2)、验证这些点的坐标是否满足函数解析式，归纳你的结论（写出自变量x的取值范围）；(3)、当指针旋转到158.4度的位置时，显示盘上的体重读数模糊不清，用解析式求出此时的体重。19. 小王周末骑电单车从家出发去商场买东西，当他骑了一段路时，想起要买一本书，于是原路返回到刚经过的新华书店，买到书店后继续前往商场，如图是他离家的距离与时间的关系示意图，请根据图中提供的信息回答下列问题：
(1)、小王从家到新华书店的路程是多少米？(2)、小王在新华书店停留了多少分钟？(3)、买到书店，小王从新华书店到商场的汽车速度是多少米/分钟？20. 小红帮弟弟荡秋千（如图1），秋千离地面的高度h（m）与摆动时间t（s）之间的关系如图2所示．
(1)、根据函数的定义，请判断变量h是否为关于t的函数？(2)、结合图象回答：①当t=0.7s时，h的值是多少？并说明它的实际意义．
②秋千摆动第一个来回需多少时间？
21. 如图1，某容器由A、B、C三个长方体组成，其中A、B、C的底面积分别为25cm2、10cm2、5cm2 ， C的容积是容器容积的 （容器各面的厚度忽略不计）．现以速度v（单位：cm3/s）均匀地向容器注水，直至注满为止．图2是注水全过程中容器的水面高度h（单位：cm）与注水时间t（单位：s）的函数图象．
(1)、在注水过程中，注满A所用时间为s，再注满B又用了s；(2)、求A的高度hA及注水的速度v；(3)、求注满容器所需时间及容器的高度．