2016-2017学年湖北省孝感市大悟县九年级上学期期中数学试卷

试卷更新日期：2017-04-12 类型：期中考试

进入出卷网下载

一、选择题

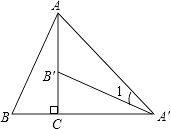
1. 关于x的一元二次方程x²﹣3x+m=0有两个不相等的实数根，则实数m的取值范围是（）

A、m＞ $\frac{9}{4}$ B、m= $\frac{9}{4}$ C、m＜ $\frac{9}{4}$ D、m＜﹣ $\frac{9}{4}$

查看试题解析
2. 如图，将Rt△ABC绕直角顶点C顺时针旋转90°，得到△A′B′C，连接AA′，若∠1=20°，则∠B的度数是（）

A、70° B、65° C、60° D、55°

查看试题解析
3. 某种花卉每盆的盈利与每盆的株数有一定的关系，每盆植3株时，平均每株盈利4元；若每盆增加1株，平均每株盈利减少0.5元，要使每盆的盈利达到15元，每盆应多植多少株？设每盆多植x株，则可以列出的方程是（）

A、（3+x）（4﹣0.5x）=15 B、（x+3）（4+0.5x）=15 C、（x+4）（3﹣0.5x）=15 D、（x+1）（4﹣0.5x）=15

查看试题解析
4. 已知二次函数的图象如图所示，则这个二次函数的表达式为（）

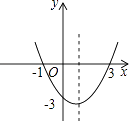A、y=x²﹣2x+3 B、y=x²﹣2x﹣3 C、y=x²+2x﹣3 D、y=x²+2x+3

查看试题解析
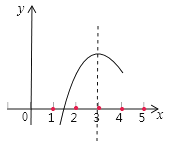
5.
如图，已知二次函数y=ax²+bx+c的部分图象，由图象可知关于x的一元二次方程ax²+bx+c=0的两个根分别是x₁=1.6，x₂=（　　）

A、﹣1.6 B、3.2 C、4.4 D、以上都不对

查看试题解析
6. 已知a是一元二次方程x²﹣x﹣1=0较大的根，则下面对a的估计正确的是（）

A、0＜a＜1 B、1＜a＜1.5 C、1.5＜a＜2 D、2＜a＜3

查看试题解析
7. 已知关于x的一元二次方程x²+ax+b=0有一个非零根﹣b，则a﹣b的值为（）

A、1 B、﹣1 C、0 D、﹣2

查看试题解析
8. 二次函数y=ax²+bx+c（a≠0）的图象如图所示，对称轴是直线x=1，则下列四个结论错误的是（）

A、c＞0 B、2a+b=0 C、b²﹣4ac＞0 D、a﹣b+c＞0

查看试题解析
9. 已知二次函数y=a（x﹣2）²+c（a＞0），当自变量x分别取 $\sqrt{2}$ 、3、0时，对应的函数值分别为y₁、y₂、y₃ ，则y₁、y₂、y₃的大小关系是（）

A、y₁＞y₂＞y₃ B、y₂＞y₁＞y₃ C、y₃＞y₁＞y₂ D、y₃＞y₂＞y₁

查看试题解析

二、填一填

10. 把方程x²+6x+3=0变形为（x+h）²=k的形式后，h= ， k= ．

查看试题解析
11. 在平面直角坐标系中，点（a，5）关于原点对称的点的坐标是（1，b+1），则点（a，b）在第象限．

查看试题解析
12. 抛物线y=ax²+bx+c上部分点的横坐标x，纵坐标y的对应值如下表：
x
…
﹣2
﹣1
0
1
2
…
y
…
0
4
6
6
4
…
则抛物线的对称轴是．

查看试题解析
13. 某小区2016年屋顶绿化面积为2000平方米，计划2018年屋顶绿化面积要达到2880平方米，如果每年屋顶绿化面积的增长率相同，那么这个增长率是．

查看试题解析
14. 如图所示的抛物线y=x²+bx+b²﹣4的图象，那么b的值是．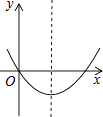

查看试题解析
15.
如图，在平面直角坐标系中，将△ABO绕点A顺时针旋转到△AB₁C₁的位置，点B、O分别落在点B₁、C₁处，点B₁在x轴上，再将△AB₁C₁绕点B₁顺时针旋转到△A₁B₁C₂的位置，点C₂在x轴上，将△A₁B₁C₂绕点C₂顺时针旋转到△A₂B₂C₂的位置，点A₂在x轴上，依次进行下去…．若点A（3，0），B（0，4），则点B₁₀₀的坐标为．

查看试题解析

三、用心做一做

16. 解下列方程：

(1)、（3x+5）²﹣（x﹣9）²=0；

(2)、3x²﹣4x﹣1=0．

查看试题解析
17.
如图：在平面直角坐标系中，网格中每一个小正方形的边长为1个单位长度，已知△ABC：

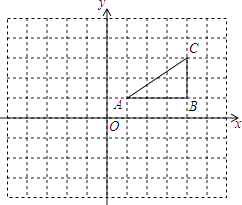(1)、作出△ABC关于点O成中心对称的图形△A₁B₁C₁ ，并写出点B对应点B₁的坐标；

(2)、作出把△ABC绕点A逆时针旋转90°后的图形△AB₂C₂ ．写出点C对应点C₂的坐标．

查看试题解析
18. 已知方程x²+（m﹣1）x+m﹣10=0的一个根是3，求m的值及方程的另一个根．

查看试题解析
19. 已知关于x的一元二次方程kx²﹣4x+2=0有实数根．

(1)、求k的取值范围；

(2)、若△ABC中，AB=AC=2，AB，BC的长是方程kx²﹣4x+2=0的两根，求BC的长．

查看试题解析
20. 如图，某小区规划在一个长40米，宽为26米的矩形场地ABCD上，修建三条同样宽的道路，使其中两条与AB平行，另一条与AD平行，其余部分种草，若使每块草坪的面积都为144平方米，求道路的宽度．

查看试题解析
21.
如图，已知二次函数y=﹣ $\frac{1}{2} x^{2}$ +bx+c的图象经过A（2，0）、B（0，﹣6）两点．

(1)、求这个二次函数的解析式；

(2)、设该二次函数的对称轴与x轴交于点C，连接BA、BC，求△ABC的面积．

查看试题解析
22.
如图，直线y=x+2与抛物线y=ax²+bx+6（a≠0）相交于A（ $\frac{1}{2}$ ， $\frac{5}{2}$ ）和B（4，m），点P是线段AB上异于A、B的动点，过点P作PC⊥x轴于点D，交抛物线于点C．

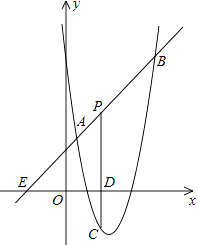(1)、求抛物线的解析式；

(2)、是否存在这样的P点，使线段PC的长有最大值？若存在，求出这个最大值；若不存在，请说明理由．

查看试题解析
23. 某企业设计了一款工艺品，每件的成本是50元，为了合理定价，投放市场进行试销．据市场调查，销售单价是100元时，每天的销售量是50件，而销售单价每降低1元，每天就可多售出5件，但要求销售单价不得低于成本．

(1)、当销售单价为70元时，每天的销售利润是多少？

(2)、求出每天的销售利润y（元）与销售单价x（元）之间的函数关系式，并求出自变量x的取值范围；

(3)、如果该企业每天的总成本不超过7000元，那么销售单价为多少元时，每天的销售利润最大？最大利润是多少？（每天的总成本=每件的成本×每天的销售量）

查看试题解析

x	…	﹣2	﹣1	0	1	2	…
y	…	0	4	6	6	4	…