2016-2017学年湖北省孝感市安陆市九年级上学期期中数学试卷

试卷更新日期：2017-04-12 类型：期中考试

进入出卷网下载

一、精心选一选。

1. 下列图形中，既是轴对称图形又是中心对称图形的是（）

A、等边三角形 B、正五边形 C、矩形 D、平行四边形

查看试题解析
2. 已知关于x的一元二次方程x²﹣x+k=0的一个根是2，则k的值是（）

A、﹣2 B、2 C、1 D、﹣1

查看试题解析
3. 将抛物线y=x²先向左平移1个单位，再向下平移2个单位得到的抛物线是（）

A、y=（x+1）²﹣2 B、y=（x﹣1）²+2 C、y=（x﹣1）²﹣2 D、y=（x+1）²+2

查看试题解析
4. 用配方法解下列方程时，配方错误的是（）

A、x²+2x﹣99=0化为（x+1）²=100 B、 $m^{2} - 7 m - 4 化为 {(m - \frac{7}{2})}^{2} = \frac{65}{4}$ C、x²+8x+9=0化为（x+4）²=25 D、 $3 x^{2} - 4 x - 2 = 0 化为 {(x - \frac{2}{3})}^{2} = \frac{10}{9}$

查看试题解析
5. 某工厂一种产品的年产量是20件，如果每一年都比上一年的产品增加x倍，两年后产品y与x的函数关系是（　　）

A、y=20（1﹣x）² B、y=20+2x C、y=20（1+x）² D、y=20+20x²+20x

查看试题解析
6.
如图，已知菱形OABC的顶点O（0，0），B（2，2），若菱形绕点O逆时针旋转，每秒旋转45°，则第60秒时，菱形的对角线交点D的坐标为（）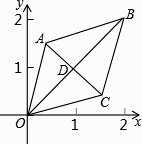

A、（1，﹣1） B、（﹣1，﹣1） C、（ $\sqrt{2}$ ，0） D、（0，﹣ $\sqrt{2}$ ）

查看试题解析
7. 有两个完全重合的矩形，将其中一个始终保持不动，另一个矩形绕其对称中心O按逆时针方向进行旋转，每次均旋转45°，第1次旋转后得到图①，第2次旋转后得到图②，…，则第10次旋转后得到的图形与图①～④中相同的是（）

A、图① B、图② C、图③ D、图④

查看试题解析
8. 二次函数y=ax²+bx+c（a≠0）和正比例函数y= $\frac{2}{3}$ x的图象如图所示，则方程ax²+（b﹣ $\frac{2}{3}$ ）x+c=0（a≠0）的两根之和（）

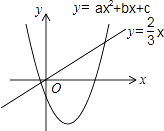A、大于0 B、等于0 C、小于0 D、不能确定

查看试题解析
9. 如图是二次函数y=ax²+bx+c（a≠0）图象的一部分，对称轴为x= $\frac{1}{2}$ ，且经过点（2，0），有下列说法：①abc＜0；②a+b=0；③4a+2b+c＜0；④若（0，y₁），（1，y₂）是抛物线上的两点，则y₁=y₂ ．上述说法正确的是（）

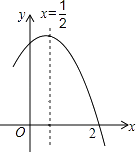A、①②④ B、③④ C、①③④ D、①②

查看试题解析

二、细心填一填。

10. 若x²=8，则x= ．

查看试题解析
11. 如图，Rt△ABC的斜边AB=16，Rt△ABC绕点O顺时针旋转后得到Rt△A′B′C′，则Rt△A′B′C′的斜边A′B′上的中线C′D的长度为．

查看试题解析
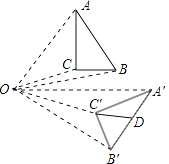12. 已知x= $\frac{- b + \sqrt{b^{2} - 4 c}}{2}$ （b²﹣4c＞0），则x²+bx+c的值为．

查看试题解析
13. 设A（﹣2，y₁），B（1，y₂），C（2，y₃）是抛物线y=﹣（x+1）²+1上的三点，则y₁ ， y₂ ， y₃的大小关系为．

查看试题解析
14. 要组织一次排球邀请赛，参赛的每两个队之间都要比赛一场．根据场地和时间等条件，赛程计划安排7天，每天安排4场比赛，设比赛组织者应邀请x个队参赛，则x满足的关系式为

查看试题解析
15. 如图所示，抛物线y=ax²+bx（a＜0）的图象与x轴交于A、O两点，顶点为B，将该抛物线的图象绕原点O旋转180°后，与x轴交于点C，顶点为D，若此时四边形ABCD恰好为矩形，则b的值为．

查看试题解析

三、用心做一做。

16. 解方程：x²+2x﹣8=0．

查看试题解析
17.
如图，已知△ABC的顶点A，B，C的坐标分别是A（﹣1，﹣1），B（﹣4，﹣3），C（﹣4，﹣1）．

(1)、作出△ABC关于原点O中心对称的图形；

(2)、将△ABC绕原点O按顺时针方向旋转90°后得到△A₁B₁C₁ ，画出△A₁B₁C₁ ，并写出点A₁的坐标．

查看试题解析
18. 已知关于x的一元二次方程x²+（m+3）x+m+1=0．

(1)、求证：无论m取何值，原方程总有两个不相等的实数根：

(2)、若x₁ ， x₂是原方程的两根，且|x₁﹣x₂|=2 $\sqrt{2}$ ，求m的值，并求出此时方程的两根．

查看试题解析
19. 如图，已知二次函数y=a（x﹣h）²+ $\sqrt{3}$ 的图象经过原点O（0，0），A（2，0）．

(1)、写出该函数图象的对称轴；

(2)、若将线段OA绕点O逆时针旋转60°到OA′，试判断点A′是否为该函数图象的顶点？

查看试题解析
20. 一幅长20cm、宽12cm的图案，如图，其中有一横两竖的彩条，横、竖彩条的宽度比为3：2．设竖彩条的宽度为xcm，图案中三条彩条所占面积为ycm² ．

(1)、求y与x之间的函数关系式；

(2)、若图案中三条彩条所占面积是图案面积的 $\frac{2}{5}$ ，求横、竖彩条的宽度．

查看试题解析
21. 如图，在四边形ABCD中，∠B+∠D=180°，AB=AD，AC=1，∠ACD=60°，求四边形ABCD的面积．

查看试题解析
22. 某商店销售面向中考生的计数跳绳，每根成本为20元，销售的前40天内的日销售量m（根）与时间t（天）的关系如表．
时间t（天）
1
3
8
10
26
…
日销售量m（件）
51
49
44
42
26
…
前20天每天的价格y₁（元/件）与时间t（天）的函数关系式为：y₁= $\frac{1}{4}$ t+25（1≤t≤20且t为整数）；后20天每天的价格y₂（元/件）与时间t（天）的函数关系式为：y₂=﹣ $\frac{1}{4}$ t+40（21≤t≤40且t为整数）．

(1)、认真分析表中的数据，用所学过的一次函数，二次函数的知识确定一个满足这些数据m（件）与t（天）之间的关系式；

(2)、请计算40天中娜一天的日销售利润最大，最大日销售利润是多少？

(3)、在实际销售的前20天中，该公司决定每销售一件商品就捐赠a元利润（a＜3）给希望工程，公司通过销售记录发现，前20天中扣除捐赠后的日销售利润随时间t（天）的增大而增大，求a的取值范围．

查看试题解析
23.
如图，抛物线L：y=ax²+bx+c与x轴交于A、B（3，0）两点（A在B的左侧），与y轴交于点C（0，3），已知对称轴x=1．

(1)、求抛物线L的解析式；

(2)、将抛物线L向下平移h个单位长度，使平移后所得抛物线的顶点落在△OBC内（包括△OBC的边界），求h的取值范围；

(3)、设点P是抛物线L上任一点，点Q在直线l：x=﹣3上，△PBQ能否成为以点P为直角顶点的等腰直角三角形？若能，求出符合条件的点P的坐标；若不能，请说明理由．

查看试题解析

时间t（天）	1	3	8	10	26	…
日销售量m（件）	51	49	44	42	26	…