2016-2017学年湖北省襄阳市保康县第一协作区九年级上学期期中数学试卷
试卷更新日期:2017-04-12 类型:期中考试
一、选择题
-
1. 一元二次方程x2﹣4=0的解是( )A、x1=2,x2=﹣2 B、x=﹣2 C、x=2 D、x1=2,x2=02.
下列图形中,中心对称图形有( )
 A、4个 B、3个 C、2个 D、1个3. 用配方法解方程:x2﹣4x+2=0,下列配方正确的是( )A、(x﹣2)2=2 B、(x+2)2=2 C、(x﹣2)2=﹣2 D、(x﹣2)2=64. 某厂一月份的总产量为500吨,三月份的总产量达到为720吨.若平均每月增长率是x , 则可以列方程( )A、500(1+2x)=720 B、500(1+x)2=720 C、500(1+x2)=720 D、720(1+x)2=5005. 我校生物兴趣小组的学生,将自己收集的标本向本组其他成员各赠送一件,全组互赠182件,如果全组有x名同学,则根据题意列出的方程是( )A、x(x+1)=182 B、x(x﹣1)=182 C、2x(x+1)=182 D、x(x﹣1)=182×26. 抛物线y=x2﹣2x+1与坐标轴交点个数为( )A、无交点 B、1个 C、2个 D、3个7. 在平面直角坐标系中,将二次函数y=2x2的图象向上平移2个单位,所得解析式为( )A、y=2x2+2 B、y=2x2﹣2 C、y=2(x+2)2 D、y=2(x﹣2)28. 已知a≠0,在同一直角坐标系中,函数y=ax与y=ax2的图象有可能是( )A、
A、4个 B、3个 C、2个 D、1个3. 用配方法解方程:x2﹣4x+2=0,下列配方正确的是( )A、(x﹣2)2=2 B、(x+2)2=2 C、(x﹣2)2=﹣2 D、(x﹣2)2=64. 某厂一月份的总产量为500吨,三月份的总产量达到为720吨.若平均每月增长率是x , 则可以列方程( )A、500(1+2x)=720 B、500(1+x)2=720 C、500(1+x2)=720 D、720(1+x)2=5005. 我校生物兴趣小组的学生,将自己收集的标本向本组其他成员各赠送一件,全组互赠182件,如果全组有x名同学,则根据题意列出的方程是( )A、x(x+1)=182 B、x(x﹣1)=182 C、2x(x+1)=182 D、x(x﹣1)=182×26. 抛物线y=x2﹣2x+1与坐标轴交点个数为( )A、无交点 B、1个 C、2个 D、3个7. 在平面直角坐标系中,将二次函数y=2x2的图象向上平移2个单位,所得解析式为( )A、y=2x2+2 B、y=2x2﹣2 C、y=2(x+2)2 D、y=2(x﹣2)28. 已知a≠0,在同一直角坐标系中,函数y=ax与y=ax2的图象有可能是( )A、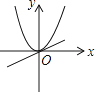 B、
B、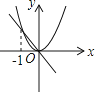 C、
C、 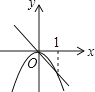 D、
D、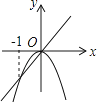 9. 设A(﹣2,y1),B(1,y2),C(2,y3)是抛物线y=﹣(x+1)2+k上的三点,则y1 , y2 , y3的大小关系为( )A、y1>y2>y3 B、y1>y3>y2 C、y2>y3>y1 D、y3>y1>y210. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列4个结论:①abc>0;②b<a+c;③4a+2b+c>0;④b2﹣4ac>0;其中正确的结论有( )
9. 设A(﹣2,y1),B(1,y2),C(2,y3)是抛物线y=﹣(x+1)2+k上的三点,则y1 , y2 , y3的大小关系为( )A、y1>y2>y3 B、y1>y3>y2 C、y2>y3>y1 D、y3>y1>y210. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列4个结论:①abc>0;②b<a+c;③4a+2b+c>0;④b2﹣4ac>0;其中正确的结论有( )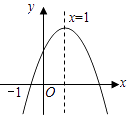 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 关于x的一元二次方程x2﹣2x+m﹣1=0有两个相等的实数根,则m的值为 .12. 点A(a,3)与点B(﹣4,b)关于原点对称,则a+b=13. 二次函数y=ax2+bx+c(a≠0)的图象的一部分,则一元二次方程的两根分别为 .
 14. 将△ABC绕着点C顺时针方向旋转50°后得到△A′B′C′.若∠A=40°,∠B′=110°,则∠BCA′的度数是 .
14. 将△ABC绕着点C顺时针方向旋转50°后得到△A′B′C′.若∠A=40°,∠B′=110°,则∠BCA′的度数是 . 15. 公路上行驶的汽车急刹车时的行驶路程s(m)与时间t(s)的函数关系式为s=20t﹣5t2 , 当遇到紧急情况时,司机急刹车,但由于惯性汽车要滑行 m才能停下来.16. 已知函数y=(k﹣3)x2+2x+1的图象与x轴有交点,则k的取值范围为 .
15. 公路上行驶的汽车急刹车时的行驶路程s(m)与时间t(s)的函数关系式为s=20t﹣5t2 , 当遇到紧急情况时,司机急刹车,但由于惯性汽车要滑行 m才能停下来.16. 已知函数y=(k﹣3)x2+2x+1的图象与x轴有交点,则k的取值范围为 .三、解方程
-
17. 解下列方程(1)、(x+4)2=5(x+4)(2)、(3x﹣2)2=(2x﹣3)2(3)、x2﹣2x﹣8=0.18. 已知关于x的方程x2+mx+m﹣2=0(1)、若该方程的一个根为1,求m的值及该方程的另一根;(2)、求证:不论m取何实数,该方程都有两个不相等的实数根.19. 如图,有一面积是150平方米的长方形鸡场,鸡场的一边靠墙(墙长18米),墙对面有一个2米宽的门,另三边用竹篱笆围成,篱笆总长33米,求:鸡场的长和宽各为多少米?
 20. 已知二次函数y=﹣x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(﹣1,0),与y轴的交点坐标为(0,3).
20. 已知二次函数y=﹣x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(﹣1,0),与y轴的交点坐标为(0,3).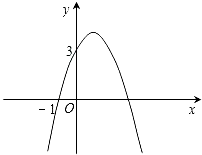 (1)、求出b,c的值,并写出此二次函数的解析式;(2)、根据图象,写出函数值y为正数时,自变量x的取值范围.21.
(1)、求出b,c的值,并写出此二次函数的解析式;(2)、根据图象,写出函数值y为正数时,自变量x的取值范围.21.如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
 (1)、请画出△ABC向左平移5个单位长度后得到的△A1B1C1;(2)、请画出△ABC关于原点对称的△A2B2C2;并写出点A2、B2、C2坐标;(3)、请画出△ABC绕O顺时针旋转90°后的△A3B3C3;并写出点A3、B3、C3坐标.22. 如图,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的,连接BE、CF相交于点D.
(1)、请画出△ABC向左平移5个单位长度后得到的△A1B1C1;(2)、请画出△ABC关于原点对称的△A2B2C2;并写出点A2、B2、C2坐标;(3)、请画出△ABC绕O顺时针旋转90°后的△A3B3C3;并写出点A3、B3、C3坐标.22. 如图,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的,连接BE、CF相交于点D.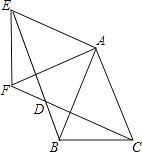 (1)、求证:BE=CF;(2)、当四边形ACDE为菱形时,求BD的长.23. 为了拉动内需,让惠于农民,丰富农民的业余生活,鼓励送彩电下乡,国家决定实行政府补贴.规定每购买一台彩电,政府补贴若干元,经调查某商场销售彩电台数y(台)与补贴款额x(元)之间大致满足如图所示的一次函数关系.随着补贴款额x的不断增大,销售量也不断增加,但每台彩电的收益p(元)会相应降低且满足:p=﹣ x+110(x≥0).
(1)、求证:BE=CF;(2)、当四边形ACDE为菱形时,求BD的长.23. 为了拉动内需,让惠于农民,丰富农民的业余生活,鼓励送彩电下乡,国家决定实行政府补贴.规定每购买一台彩电,政府补贴若干元,经调查某商场销售彩电台数y(台)与补贴款额x(元)之间大致满足如图所示的一次函数关系.随着补贴款额x的不断增大,销售量也不断增加,但每台彩电的收益p(元)会相应降低且满足:p=﹣ x+110(x≥0). (1)、在政府补贴政策实施后,求出该商场销售彩电台数y与政府补贴款额x之间的函数关系式;(2)、在政府未出台补贴措施之前,该商场销售彩电的总收益额为多少元?(3)、要使该商场销售彩电的总收益最大,政府应将每台补贴款额x定为多少?并求出总收益的最大值.24.
(1)、在政府补贴政策实施后,求出该商场销售彩电台数y与政府补贴款额x之间的函数关系式;(2)、在政府未出台补贴措施之前,该商场销售彩电的总收益额为多少元?(3)、要使该商场销售彩电的总收益最大,政府应将每台补贴款额x定为多少?并求出总收益的最大值.24.边长为2的正方形OABC在平面直角坐标系中的位置如图所示,点D是边OA的中点,连接CD,点 E在第一象限,且DE⊥DC,DE=DC.以直线AB为对称轴的抛物线过C,E两点.
 (1)、求E点坐标;(2)、设抛物线的解析式为y=a(x﹣h)2+k,求a,h,k;(3)、点M为直线AB上一动点,点N为抛物线上一动点,是否存在点M,N,使得以点M,N,D,E为顶点的四边形是平行四边形?若存在,请直接写出满足条件的点M,N的坐标;若不存在,请说明理由.
(1)、求E点坐标;(2)、设抛物线的解析式为y=a(x﹣h)2+k,求a,h,k;(3)、点M为直线AB上一动点,点N为抛物线上一动点,是否存在点M,N,使得以点M,N,D,E为顶点的四边形是平行四边形?若存在,请直接写出满足条件的点M,N的坐标;若不存在,请说明理由.