2016-2017学年湖北省武汉市江岸区九年级上学期期中数学试卷
试卷更新日期：2017-04-12 类型：期中考试
一、选择题
-
1. 下列图形中，既是轴对称图形又是中心对称图形的是（ ）A、
B、
C、
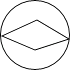D、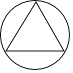
2. 一元二次方程x2﹣2x=0的根是（ ）A、2 B、0 C、0和2 D、13. 若关于x的函数y=（2﹣a）x2﹣x是二次函数，则a的取值范围是（ ）A、a≠0 B、a≠2 C、a＜2 D、a＞24. 已知方程2x2﹣x﹣1=0的两根分别是x1和x2 ， 则x1+x2的值等于（ ）A、2 B、﹣ C、 D、﹣15. 如图，在△ABC中，C=90°，AC=3，BC=4，将△ABC绕A逆时针旋转，使点C落在线段AB上的点E处，点B落在点D处，则线段BE的长度为（ ）
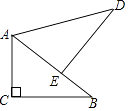A、2 B、3 C、4 D、26. 如图，在⊙O中，∠AOB=120°，P为弧AB上的一点，则∠APB的度数是（ ）
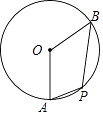A、100° B、110° C、120° D、130°7. 将二次函数y=x2的图象向右平移1个单位，再向上平移2个单位后，所得图象的函数表达式是（ ）A、y=（x﹣1）2+2 B、y=（x+1）2+2 C、y=（x﹣1）2﹣2 D、y=（x+1）2﹣28. 九年级某班在期中考试前，每个同学都向全班其他同学各送一张写有祝福的卡片，全班共送了1190张卡片，设全班有x名学生，根据题意列出方程为（ ）A、 x（x﹣1）=1190 B、 x（x+1）=1190 C、x（x+1）=1190 D、x（x﹣1）=11909. 如图，△ABC内接于⊙O，AB是⊙O的直径，CE平分∠ACB交⊙O于点E，∠E=30°，交AB于点D，连接AE，则SADC：S△ADE的比值为（ ）
A、 B、 C、 D、110. 二次函数y=ax2+bx+c（a≠0）的大致图象如图所示（1＜x=h＜2，0＜xA＜1）．下列结论：①2a+b＞0；②abc＜0； ③若OC=2OA，则2b﹣ac=4； ④3a﹣c＜0．其中正确的个数是（ ）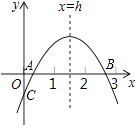
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 点A（2，﹣1）关于原点对称的点B的坐标为 ．12. 将二次函数y=x2﹣2x化为顶点式的形式为： ．13. 若关于x的方程﹣x2+5x+c=0的一个根为3，则c= ．14. 已知同一平面内存在⊙O和点P，点P与⊙O上的点的最大距离为8，最小距离为2，则⊙O的半径为 ．15. 将函数y=x2的图象向右平移2个单位得函数y1的图象，将y与y1合起来构成新图象，直线y=m被新图象依次截得三段的长相等，则 ．16. 在△ABC中，∠BAC=90°，AB=AC=2cm，线段BC上一动点P从C点开始运动，到B点停止，以AP为边在AC的右侧作等边△APQ，则Q点运动的路径为 cm．
三、解答题
-
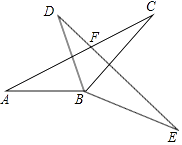
17. 解方程：x2﹣2x﹣3=0；18. 如图，将△ABC绕点B顺时针旋转60°后得到△DBE（点A对应点为D），线段AC交线段DE于点F，求∠EFC的度数．
19. 已知抛物线y=﹣x2+bx+c的部分图象如图所示，A（1，0），B（0，3）．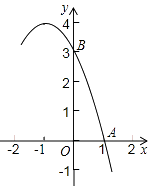
(1)、求抛物线的解析式；(2)、结合函数图象，写出当y＜3时x的取值范围．
20. 如图，在正方形网格中，每一小正方形的边长为1，格点ABC（三个顶点在相应的正方形的顶点处）在如图所示的位置：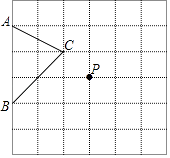
(1)、△ABC的面积为：；(2)、在网格中画出线段AB绕格点P顺时针旋转90°之后的对应线段A1B1；(3)、在（2）的基础上，直接写出 = ．
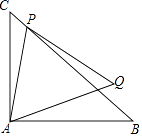
21. 如图，AB为⊙O的直径，点C为半圆上一点，AD平分∠CAB交⊙O于点D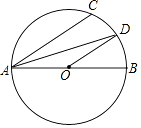
(1)、求证：OD∥AC；(2)、若AC=8，AB=10，求AD．22. 某宾馆有50个房间供游客住宿，当每个房间的房价为每天180元时，房间会全部住满．当每个房间每天的房价每增加10元时，就会有一个房间空闲．宾馆需对游客居住的每个房间每天支出20元的各种费用．根据规定，每个房间每天的房价不得高于340元．设每个房间的房价增加x元（x为10的正整数倍）．(1)、设一天订住的房间数为y，直接写出y与x的函数关系式及自变量x的取值范围；(2)、设宾馆一天的利润为w元，求w与x的函数关系式；(3)、一天订住多少个房间时，宾馆的利润最大？最大利润是多少元？23. 已知矩形ABCD，点P为BC边上一动点，连接AP，将线段AP绕P点顺时针旋转90°，点A恰好落在直线CD上点E处．(1)、如图1，点E在线段CD上，求证：AD+DE=2AB；
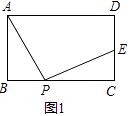(2)、如图2，点E在线段CD的延长线上，且点D为线段CE的中点，在线段BD上取点F，连接AF、PF，若AF=AB．求证：∠APF=∠ADB．
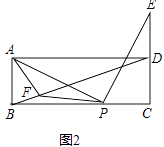(3)、如图3，点E在线段CD上，连接BD，若AB=2，BD∥PE，则DE= ． （直接写出结果）
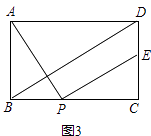24. 已知抛物线C1：y=﹣ x2+mx+m+ ．(1)、①无论m取何值，抛物线经过定点P；②随着m的取值变化，顶点M（x，y）随之变化，y是x的函数，则其函数C2关系式为；
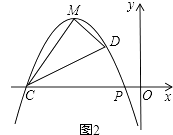
(2)、如图1，若该抛物线C1与x轴仅有一个公共点，请在图1中画出顶点M满足的函数C2的大致图象，平行于y轴的直线l分别交C1、C2于点A、B，若△PAB为等腰直角三角形，判断直线l满足的条件，并说明理由；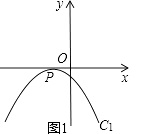
(3)、如图2，抛物线C1的顶点M在第二象限，交x轴于另一点C，抛物线上点M与点P之间一点D的横坐标为﹣2，连接PD、CD、CM、DM，若S△PCD=S△MCD ， 求二次函数的解析式．
