2016-2017学年河北省唐山市路南区九年级上学期期中数学试卷

试卷更新日期：2017-04-12 类型：期中考试

进入出卷网下载

一、选择题

1. 若（k﹣1）x²﹣2kx﹣1=0是关于x的一元二次方程，则k的取值范围是（）

A、k≠﹣1 B、k≠1 C、k≠0 D、k≥1

查看试题解析
2. 在平面直角坐标系中，把点P（﹣2，1）绕原点O顺时针旋转180°，所得到的对应点P′的坐标为（）

A、（2，﹣1） B、（﹣2，1） C、（2，1） D、（﹣2，﹣1）

查看试题解析
3. 把方程x²﹣8x+3=0配方成如下的形式，则正确是（）

A、（x+4）²=13 B、（x﹣4）²=19 C、（x﹣4）²=13 D、（x+4）²=19

查看试题解析
4. 下列变换不属于全等变换的是（）

A、平移 B、旋转 C、轴对称 D、相似

查看试题解析
5. 如图，⊙O△ABC的三条边所得的弦长相等，则下列说法正确的是（）

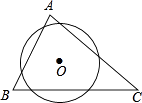A、点O是△ABC的内心 B、点O是△ABC的外心 C、△ABC是正三角形 D、△ABC是等腰三角形

查看试题解析
6. 已知a，b，c，d是成比例线段，其中a=3cm，b=2cm，c=6cm，则d的长度为（）

A、4cm B、5cm C、6cm D、9cm

查看试题解析
7. 下列表格是二次函数y=ax²+bx+c（d≠0）的自变量x与函数y的一些对应值，由此可以判断方程ax²+bx+c=0（a≠0）的一个根在（）
x
6.17
6.18
6.19
6.20
y=ax²+bx+c
﹣0.03
﹣0.01
0.02
0.06

A、﹣0.01﹣0.02之间 B、0.02﹣0.06之间 C、6.17﹣6.18之间 D、6.18﹣6.19之间

查看试题解析
8. 如图，AD∥BE∥CF，直线l₁ ， l₂与这三条平行线分别交于点A，B，C，D，E，F， $\frac{A B}{B C}$ = $\frac{2}{3}$ ，DE=6，则EF的值为（）

A、4 B、6 C、9 D、12

查看试题解析
9. 已知抛物线y=ax²﹣2x+1与x轴有两个交点，那么a的取值范围是（）

A、a＜1且a≠0 B、a＞1且a≠2 C、a≥1且a≠2 D、a≤1且a≠0

查看试题解析
10. 如图，BD是⊙O的直径，点A、C在圆上，且CD=OB，则∠DAC等于（）

A、90° B、60° C、45° D、30°

查看试题解析
11.
已知二次函数y=ax²+bx+c（a≠0）的图象如图所示，则下列结论：
（1）若点（x₁ ， y₁），（x₂ ， y₂）在图象上，当x₂＞x₁＞0时，y₂＞y₁；
（2）当x＜﹣1时，y＞0；
（3）4a+2b+c＞0；
（4）x=3是关于x方程ax²+bx+c=0的一个根，其中正确的个数为（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

12. 把方程x（x+1）=2化成一般形式是．

查看试题解析
13. 抛物线y=（﹣x）²开口向（填：“上”或“下”）

查看试题解析
14. 如图，用一个半径为30cm扇形铁皮，制作一个无底的圆锥（不计损耗），经测量圆锥的底面半径r为10cm，则扇形铁皮的面积为 cm² ．（结果保留π）

查看试题解析
15. 已知x=1是一元二次方程ax²+bx﹣10=0的一个根，则分式 $\frac{a^{2} + 2 a b + b^{2}}{2 a + 2 b}$ 的值为．

查看试题解析
16. 如图，边长为1的正五边形ABCDE，顶点A、B在半径为1的圆上，其它各点在圆内，将正五边形ABCDE绕点A逆时针旋转，当点E第一次落在圆上时，则点C转过的度数为．

查看试题解析
17. 如图是某地一座抛物线形拱桥，桥拱在竖直平面内，与水平桥面相交于A、B两点，拱桥最高点C到AB的距离为4m，AB=12m，D、E为拱桥底部的两点，且DE∥AB，点E到直线AB的距离为5m，则DE的长为 m．

查看试题解析

三、解答题

18. 解下列方程：

(1)、x²+x=0；

(2)、x²﹣4x﹣1=0．

查看试题解析
19. 如图为一段圆弧形弯道，弯道长12π米，圆弧所对的圆心角是81°．

(1)、用直尺和圆规作出圆弧所在的圆心O；（不写作法，保留作图痕迹）

(2)、求这段圆弧的半径R．

查看试题解析
20. 如图，在平面直角坐标系xOy中，点O是边长为2的正方形ABCD的中心．

(1)、若函数y=x²+m的图象过点C，求这个函数的解析式；并判断其函数图象是否过A点．

(2)、若将（1）中的函数图象先向右平移1个单位，再向上平移2个单位，直接写出平移后函数的解析式和顶点坐标．

查看试题解析
21. 如图，在长60m，宽40m的长方形花园中，欲修宽度相等的观赏路（图中阴影部分），要使观赏路面积占总面积的 $\frac{7}{16}$ ，求观赏路面宽是多少m．

查看试题解析
22. 抛物线y=ax²+bx+c上，部分点的横、纵坐标x、y的对应值如下表：
x
…
﹣2
﹣1
0
1
2
…
y
…
0
﹣4
﹣4
0
8

(1)、根据上表填空；
①方程ax²+bx+c=0的两个根分别是和．
②抛物线经过点（﹣3，）；
③在对称轴左侧，y随x增大而；

(2)、求抛物线y=ax²+bx+c的解析式．

查看试题解析
23. 如图，△OAB中，OA=OB=10，∠AOB=70°，以点O为圆心，6为半径的优弧 $\hat{M N}$ 分别交OA、OB于点M，N．

(1)、点P在右半弧上（∠BOP是锐角），将OP绕点O逆时针旋转70°得OP′．求证：AP=BP′；

(2)、点T在左半弧上，若AT与弧相切，求点T到OA的距离；

(3)、设点Q在优弧 $\hat{M N}$ 上，当△AOQ的面积最大时，直接写出∠BOQ的度数．

查看试题解析
24. 【探究】中秋节前某商场计划购进一批进价为每盒40元的食品进行销售，根据销售经验，应季销售时，若每盒食品的售价为60元，则可售出400盒，当每盒食品的售价每提高1元，销售量就相应减少10盒．

(1)、假设每盒食品的售价提高x元，那么销售每盒食品所获得的利润是元，销售量是盒．（用含x为代数式表示）

(2)、设应季销售利润为y元，求y与x的函数关系式，并求出应季销售利润为8000元时每盒食品的售价．

(3)、【拓展】根据销售经验，过季处理时，若每盒食品的售价定为30元亏本销售，可售出50盒，若每盒食品的售价每降低1元，销售量就相应增加5盒．当单价降低z元时，解答：
现剩余100盒食品需要处理，经过降价处理后还是无法销售的只能积压在仓库，损失本金，若使亏损金额最小，此时每盒食品的售价应为元；

(4)、若过季需要处理的食品共m盒，过季处理时亏损金额为y₁元，求y₁与z的函数关系式；当100≤m≤300时，求过季销售亏损金额最小时多少元？

查看试题解析

x	6.17	6.18	6.19	6.20
y=ax²+bx+c	﹣0.03	﹣0.01	0.02	0.06

x	…	﹣2	﹣1	0	1	2	…
y	…	0	﹣4	﹣4	0	8