2016-2017学年广西玉林市博白县九年级上学期期中数学试卷
试卷更新日期：2017-04-12 类型：期中考试
一、选择题
-
1. 下列方程中，关于x的一元一次方程是（ ）A、x2+2x=x2﹣1 B、 + ﹣2=0 C、ax2+bx+c=0 D、（x+1）2=2（x+1）2. 一元二次方程（x﹣1）2=0的解为（ ）A、x=1 B、x=0 C、x=﹣1 D、x=±13. 将图中所示的图案以圆心为中心，旋转180°后得到的图案是（ ）
A、
B、
C、
D、
4. 点P（﹣2，1）关于原点对称的点的坐标是（ ）A、（2，1） B、（2，﹣1） C、（﹣1，2） D、（1，﹣2）5. 已知一元二次方程x2﹣4x+3=0两根为x1、x2 ， 则x1•x2=（ ）A、3 B、4 C、﹣4 D、﹣36. 关于x的一元二次方程（a﹣1）x2+x+a2﹣1=0的一个根是0，则a的值为（ ）A、1 B、﹣1 C、1或﹣1 D、07. 函数y=x2﹣3x+4的图象与坐标轴的交点个数是（ ）A、0个 B、1个 C、2个 D、3个8. 在同一平面直角坐标系中，函数y=ax+b与y=ax2﹣bx的图象可能是（ ）A、
B、
C、
D、
9. 如图，在等边三角形ABC中，AB=6，D是BC上一点，且BC=3BD，△ABD绕点A旋转后得到△ACE，则CE的长度为（ ）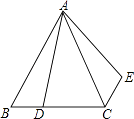
A、6 B、5 C、3 D、210. 若二次函数y=x2﹣6x+c的图象过A（﹣1，y1），B（2，y2），C（3，y3），则y1、y2、y3的大小关系是（ ）A、y1＞y2＞y3 B、y1＞y3＞y2 C、y2＞y1＞y3 D、y3＞y1＞y211. 有一人患了流感，经过两轮传染后共有100人患了流感，那么每轮传染中，平均一个人传染的人数为（ ）A、8人 B、9人 C、10人 D、11人12. 如图，二次函y=ax2+bx+c（a≠0）图象的一部分，对称轴为直线x= ，且经过点（2，0），下列说法：①abc＜0；
②a+b=0；
③4a+2b+c＜0；
④若（﹣2，y1），（﹣3，y2）是抛物线上的两点，则y1＜y2 ，
其中说法正确的是（ ）
A、①②④ B、③④ C、①③④ D、①②二、填空题
-
13. 二次函数y=2（x﹣3）2﹣4的最小值为 ．14.
如图，在平面直角坐标系中，将线段AB绕点A按逆时针方向旋转90°后，得到线段AB′，则点B′的坐标为 ．
15. 如果关于x的方程x2﹣3x+k=0有两个相等的实数根，那么实数k的值是 ．16. 已知二次函数y=ax2+bx+c的图象如图所示，则点P（a，bc）在第象限．
17. 如图是一张长9cm、宽5cm的矩形纸板，将纸板四个角各剪去一个同样的正方形，可制成底面积是12cm2的一个无盖长方体纸盒，设剪去的正方形边长为xcm，则可列出关于x的方程为 ．
18. 如图，四边形ABCD是菱形，O是两条对角线的交点，过O点的三条直线将菱形分成阴影和空白部分．当菱形的两条对角线的长分别为6和8时，则阴影部分的面积为 ．
三、解答题
-
19. 解方程：3（x﹣2）2=2（2﹣x）．20. 已知方程5x2+kx﹣6=0的一根是2，求它的另一根及k的值．21. 已知实数x，y满足x2﹣6x+ +9=0，则（x+y）2016的值是多少？22. 已知二次函数y=x2+mx+n的图象经过点P（﹣3，1），对称轴是直线x=﹣1．(1)、求m，n的值；(2)、x取什么值时，y随x的增大而减小？23.
已知：△ABC在坐标平面内，三个顶点的坐标分别为A（0，3），B（3，4），C（2，2）．（正方形网格中，每个小正方形的边长是1个单位长度）
(1)、画出△ABC向下平移4个单位，再向左平移1个单位得到的△A1B1C1 ， 并直接写出C1点的坐标；(2)、作出△ABC绕点A顺时针方向旋转90°后得到的△A2B2C2 ， 并直接写出C2点的坐标；(3)、作出△ABC关于原点O成中心对称的△A3B3C3 ， 并直接写出B3的坐标．24. 某宾馆有客房200间供游客居住，当每间客房的定价为每天180元时，客房恰好全部住满；如果每间客房每天的定价每增加10元，就会减少4间客房出租．设每间客房每天的定价增加x元，宾馆出租的客房为y间．求：(1)、y关于x的函数关系式；(2)、如果某天宾馆客房收入38400元，那么这天每间客房的价格是多少元？
