2018-2019学年初中数学浙教版八年级下册2.3 一元二次方程的应用 同步练习
试卷更新日期:2019-01-17 类型:同步测试
一、单选题
-
1. 随着台州市打造“和合圣地”的推进,某企业推出以“和合文化”为载体的产品,2017年盈利50万元,计划到2019年盈利84.5万元,则该产品的年平均增长率为( )
A、20% B、30% C、34.5% D、69%2. 某市体育局要组织一次篮球邀请赛,赛制为单循环形式(每两队之间都赛一场),计划安排28场比赛,设应邀请x个球队参加比赛,则可列方程为( )A、(x−1)x=28 B、(x+1)x=28 C、 (x−1)x=28 D、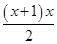 =28
3. 九年级(1)班有若干人,新年互送贺年卡一张,已知全班共送贺年卡2970张,则这个班共有( )A、54人 B、55人 C、56人 D、57人4. 如图,在一块长为22米、宽为17米的长方形地面上,要修建同样宽的两条互相垂直的道路(两条道路各与长方形的一条边平行),剩余部分种上草坪,使草坪面积为300平方米.若设道路宽为x米,则根据题意可列出方程为( )
=28
3. 九年级(1)班有若干人,新年互送贺年卡一张,已知全班共送贺年卡2970张,则这个班共有( )A、54人 B、55人 C、56人 D、57人4. 如图,在一块长为22米、宽为17米的长方形地面上,要修建同样宽的两条互相垂直的道路(两条道路各与长方形的一条边平行),剩余部分种上草坪,使草坪面积为300平方米.若设道路宽为x米,则根据题意可列出方程为( ) A、
A、 B、
B、 C、
C、 D、
D、 5. 新华商场销售某种冰箱,每台进货价为2500元.市场调研表明:当销售价为2900元时,平均每天能售出8台;而当销售价每降低50元时,平均每天就能多售出4台.商场要想使这种冰箱的销售利润平均每天达到5000元,设每台冰箱的定价为x元,则x满足的关系式为( )
5. 新华商场销售某种冰箱,每台进货价为2500元.市场调研表明:当销售价为2900元时,平均每天能售出8台;而当销售价每降低50元时,平均每天就能多售出4台.商场要想使这种冰箱的销售利润平均每天达到5000元,设每台冰箱的定价为x元,则x满足的关系式为( )
A、(x−2500)(8+4× )=5000 B、(2900−x−2500)(8+4× )=5000 C、(x−2500)(8+4× )=5000 D、(2900−x)(8+4× )=50006. 宾馆有50间房供游客居住,当毎间房每天定价为180元时,宾馆会住满;当毎间房每天的定价每增加10元时,就会空闲一间房.如果有游客居住,宾馆需对居住的毎间房每天支出20元的费用.当房价定为多少元时,宾馆当天的利润为10890元?设房价定为x元.则有( )A、(180+x﹣20)(50﹣ )=10890 B、(x﹣20)(50﹣ )=10890 C、x(50﹣ )﹣50×20=10890 D、(x+180)(50﹣ )﹣50×20=108907. 我市某楼盘准备以每平方米6000元的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望,为了加快资金周转,房地产开发商对价格经过连续两次下调后,决定以每平方米4860元的均价开盘销售,则平均每次下调的百分率是( )。
A、8% B、9% C、10% D、11%8. 某中学组织初三学生篮球比赛,以班为单位,每两班之间都比赛一场,计划安排15场比赛,则共有多少个班级参赛?( )
A、4 B、5 C、6 D、79. 在一次酒会上,每两人都只碰一次杯,如果一共碰杯55次,则参加酒会的人数为( )A、9人 B、10人 C、11人 D、12人10. 如图,将矩形沿图中虚线(其中 )剪成四块图形,用这四块图形恰能拼成一个正方形.若 ,则 的值为( )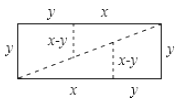 A、3 B、 C、 D、
A、3 B、 C、 D、二、填空题
-
11. 由于甲型H1N1流感(起初叫猪流感)的影响,在一个月内猪肉价格两次大幅下降.由原来每斤16元下调到每斤9元,求平均每次下调的百分率是多少?设平均每次下调的百分率为 ,则根据题意可列方程为 .
12. 网民小李的QQ群里共有若干个好友,每个好友都分别给群里其他好友发送了一条消息,这样共有90条消息,设小李的QQ群里共有好友x个,可列方程为: .13. 要设计一幅长 ,宽 的图案,制成一幅矩形挂图,如图所示,其中有两横两竖的彩条(横竖彩条的宽度相等).如果要使彩条所占面积是图案面积的四分之一,应如何设计彩条的宽度?设彩条的宽为 ,那么 满足的方程为 . 14. 如图所示,1条直线将平面分成2个部分,2条直线最多可将平面分成4个部分,3条直线最多可将平面分成7个部分,4条直线最多可将平面分成11个部分.现有n条直线最多可将平面分成56个部分,则n的值为 .
14. 如图所示,1条直线将平面分成2个部分,2条直线最多可将平面分成4个部分,3条直线最多可将平面分成7个部分,4条直线最多可将平面分成11个部分.现有n条直线最多可将平面分成56个部分,则n的值为 . 15. 某剧院举办文艺演出.经调研,如果票价定为每张30元,那么1200张门票可以全部售出;如果票价每增加1元,那么售出的门票就减少20张.要使门票收入达到38500元,票价应定为多少元?若设票价为x元,则可列方程为 .16. 某商场销售一批电视机,一月份每台毛利润是售出价的20%(毛利润=售出价-买入价),二月份该商场将每台售出价调低10%(买入价不变),结果销售台数比一月份增加120%,那么二月份的毛利润总额与一月份毛利润总额的比是
15. 某剧院举办文艺演出.经调研,如果票价定为每张30元,那么1200张门票可以全部售出;如果票价每增加1元,那么售出的门票就减少20张.要使门票收入达到38500元,票价应定为多少元?若设票价为x元,则可列方程为 .16. 某商场销售一批电视机,一月份每台毛利润是售出价的20%(毛利润=售出价-买入价),二月份该商场将每台售出价调低10%(买入价不变),结果销售台数比一月份增加120%,那么二月份的毛利润总额与一月份毛利润总额的比是
三、解答题
-
17. 桂林市新建的汽车南站站前广场需要绿化。该项绿化工程中有一块长为20 m,宽为8m的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为56m2 , 两块绿地之间及周边留有宽度相等的人行通道(如图所示),问人行通道的宽度是多少米?
 18. 某花圃用花盆培育某种花苗,经过实验发现每盆的盈利与每盆的株数构成一.定的关系。每盆植人3株时,平均单株盈利4元;以同样的裁培条件若每盆每增加1株,平均单株盈利就减少0.5元要使每盆的盈利达到14元,且尽可能地减少成本,每盆应该植多少株?19. 如图①,窗帘的褶皱是指按照窗户的实际宽度将窗帘布料以一定比例加宽的做法,褶皱之后的窗帘更能彰显其飘逸、灵动的效果.其中,窗宽度的1.5倍为平褶皱,窗宽度的2倍为波浪褶皱.如图②,小莉房间的窗户呈长方形,窗户的宽度(AD)比高度(AB)的少0.5m,某种窗帘的价格为120元/m2 . 如果以波浪褶皱的方式制作该种窗帘比以平褶皱的方式费用多180元,求小莉房间窗户的宽度与高度.
18. 某花圃用花盆培育某种花苗,经过实验发现每盆的盈利与每盆的株数构成一.定的关系。每盆植人3株时,平均单株盈利4元;以同样的裁培条件若每盆每增加1株,平均单株盈利就减少0.5元要使每盆的盈利达到14元,且尽可能地减少成本,每盆应该植多少株?19. 如图①,窗帘的褶皱是指按照窗户的实际宽度将窗帘布料以一定比例加宽的做法,褶皱之后的窗帘更能彰显其飘逸、灵动的效果.其中,窗宽度的1.5倍为平褶皱,窗宽度的2倍为波浪褶皱.如图②,小莉房间的窗户呈长方形,窗户的宽度(AD)比高度(AB)的少0.5m,某种窗帘的价格为120元/m2 . 如果以波浪褶皱的方式制作该种窗帘比以平褶皱的方式费用多180元,求小莉房间窗户的宽度与高度.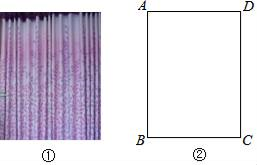 20. 为了巩固全国文明城市建设成果,突出城市品质的提升,近年来,我市积极落实节能减排政策,推行绿色建筑,据统计,我市2016年的绿色建筑面积约为950万平方米,2018年达到了1862万平方米.若2017年、2018年的绿色建筑面积按相同的增长率逐年递增,请解答下列问题:(1)、求这两年我市推行绿色建筑面积的年平均增长率;(2)、2019年我市计划推行绿色建筑面积达到2400万平方米.如果2019年仍保持相同的年平均增长率,请你预测2019年我市能否完成计划目标?21. 小明锻炼健身,从A地匀速步行到B地用时25分钟.若返回时,发现走一小路可使A、B两地间路程缩短200米,便抄小路以原速返回,结果比去时少用2.5分钟.(1)、求返回时A、B两地间的路程;(2)、若小明从A地步行到B地后,以跑步形式继续前进到C地(整个锻炼过程不休息).据测试,在他整个锻炼过程的前30分钟(含第30分钟),步行平均每分钟消耗热量6卡路里,跑步平均每分钟消耗热量10卡路里;锻炼超过30分钟后,每多跑步1分钟,多跑的总时间内平均每分钟消耗的热量就增加1卡路里.测试结果,在整个锻炼过程中小明共消耗904卡路里热量.问:小明从A地到C地共锻炼多少分钟?22. 如图,在△ABC中,∠B=90°,AB=6厘米,BC=8厘米.点P从A点开始沿A边向点B以1厘米/秒的速度移动(到达点B即停止运动),点Q从B点开始沿BC边向点C以2厘米/秒的速度移动(到达点C即停止运动).
20. 为了巩固全国文明城市建设成果,突出城市品质的提升,近年来,我市积极落实节能减排政策,推行绿色建筑,据统计,我市2016年的绿色建筑面积约为950万平方米,2018年达到了1862万平方米.若2017年、2018年的绿色建筑面积按相同的增长率逐年递增,请解答下列问题:(1)、求这两年我市推行绿色建筑面积的年平均增长率;(2)、2019年我市计划推行绿色建筑面积达到2400万平方米.如果2019年仍保持相同的年平均增长率,请你预测2019年我市能否完成计划目标?21. 小明锻炼健身,从A地匀速步行到B地用时25分钟.若返回时,发现走一小路可使A、B两地间路程缩短200米,便抄小路以原速返回,结果比去时少用2.5分钟.(1)、求返回时A、B两地间的路程;(2)、若小明从A地步行到B地后,以跑步形式继续前进到C地(整个锻炼过程不休息).据测试,在他整个锻炼过程的前30分钟(含第30分钟),步行平均每分钟消耗热量6卡路里,跑步平均每分钟消耗热量10卡路里;锻炼超过30分钟后,每多跑步1分钟,多跑的总时间内平均每分钟消耗的热量就增加1卡路里.测试结果,在整个锻炼过程中小明共消耗904卡路里热量.问:小明从A地到C地共锻炼多少分钟?22. 如图,在△ABC中,∠B=90°,AB=6厘米,BC=8厘米.点P从A点开始沿A边向点B以1厘米/秒的速度移动(到达点B即停止运动),点Q从B点开始沿BC边向点C以2厘米/秒的速度移动(到达点C即停止运动). (1)、如果P、Q分别从A、C两点同时出发,经过几秒钟,△PBQ的面积等于是△ABC的三分之一?(2)、如果P、Q两点分别从A、C两点同时出发,而且动点P从A点出发,沿AB移动(到达点B即停止运动),动点Q从B出发,沿BC移动(到达点C即停止运动),几秒钟后,P、Q相距6厘米?(3)、如果P、Q两点分别从A、C两点同时出发,而且动点P从A点出发,沿AB移动(到达点B即停止运动),动点Q从C出发,沿CB移动(到达点B即停止运动),是否存在一个时刻,PQ同时平分△ABC的周长与面积?若存在求出这个时刻的t值,若不存在说明理由.
(1)、如果P、Q分别从A、C两点同时出发,经过几秒钟,△PBQ的面积等于是△ABC的三分之一?(2)、如果P、Q两点分别从A、C两点同时出发,而且动点P从A点出发,沿AB移动(到达点B即停止运动),动点Q从B出发,沿BC移动(到达点C即停止运动),几秒钟后,P、Q相距6厘米?(3)、如果P、Q两点分别从A、C两点同时出发,而且动点P从A点出发,沿AB移动(到达点B即停止运动),动点Q从C出发,沿CB移动(到达点B即停止运动),是否存在一个时刻,PQ同时平分△ABC的周长与面积?若存在求出这个时刻的t值,若不存在说明理由.