2018-2019学年初中数学浙教版八年级下册2.2 一元二次方程的解法同步练习

试卷更新日期：2019-01-17 类型：同步测试

进入出卷网下载

一、单选题

1. 一元二次方程x²＝x的根是（）

A、x₁＝0，x₂＝1 B、x₁＝0，x₂＝－1 C、x₁＝x₂＝0 D、x₁＝x₂＝1

查看试题解析
2. 若 $2 x + 1$ 与 $2 x - 1$ 互为倒数，则实数 $x$ 为（）

A、± $\frac{1}{2}$ B、±1 C、± $\frac{\sqrt{2}}{2}$ D、± $\sqrt{2}$

查看试题解析
3. 一元二次方程y²﹣y﹣ $\frac{3}{4}$ =0配方后可化为（）

A、（y+ $\frac{1}{2}$ ）²=1 B、（y﹣ $\frac{1}{2}$ ）²=1 C、（y+ $\frac{1}{2}$ ）²= $\frac{3}{4}$ D、（y﹣ $\frac{1}{2}$ ）²= $\frac{3}{4}$

查看试题解析
4. 小丽同学想用公式法解方程-x²+3x=1，你认为a、b、c的值应分别为（）

A、 $- 1$ 、3、 $- 1$ B、 $- 1$ 、3、1 C、 $- 1$ 、 $- 3$ 、 $- 1$ D、 1、 $- 3$ 、 $- 1$

查看试题解析
5. 若一元二次方程 $x^{2} + b x + 5 = 0$ 配方后为 ${(x - 3)}^{2} = k$ ，则b，k的值分别为（）

A、-6，4 B、6，4 C、6，13 D、-6，13

查看试题解析
6. 一个三角形的两边长为3和8，第三边的长是方程x(x-9)-13(x-9)=0的根，则这个三角形的周长是（）

A、20 B、20或24 C、9和13 D、24

查看试题解析
7. 一元二次方程(x＋6)²＝16可化为两个一元一次方程，其中一个一元一次方程是x＋6＝4，则另一个一元一次方程是（）

A、x－6＝4 B、x－6＝－4 C、x＋6＝4 D、x＋6＝－4

查看试题解析
8. 用公式法解方程3x²+4=12x，下列代入公式正确的是（）

A、 $x = \frac{12 \pm \sqrt{12^{2} - 3 \times 4}}{2}$ B、x $= \frac{- 12 \pm \sqrt{12^{2} - 3 \times 4}}{2}$ C、 $x = \frac{- 12 \pm \sqrt{- {(- 12)}^{2} - 3 \times 4}}{2}$ D、 $x = \frac{- (- 12) \pm \sqrt{{(- 12)}^{2} - 3 \times 4}}{2}$

查看试题解析
9. 下列一元二次方程中，没有实数根的是（）

A、 B、 C、 D、

查看试题解析
10. 如图，将图甲表示的正方形纸片剪成四块，恰好拼成图乙表示的矩形.若x=1，则y等于（）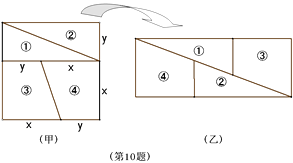

A、 $\frac{\sqrt{5} - 1}{2}$ B、 $\frac{\sqrt{5} + 1}{2}$ C、 $\frac{3 - \sqrt{5}}{2}$ D、 $\sqrt{2} + 1$

查看试题解析
11. 一元二次方程 $x^{2} + 2 x - \frac{5}{4} = 0$ 的根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法判断

查看试题解析
12. 若关于 $x$ 的一元二次方程 ${kx}^{2} - 4 x + 3 = 0$ 有实数根，则 $k$ 的非负整数值是（）

A、1 B、0,1 C、1,2 D、1,2,3

查看试题解析

二、填空题

13. 方程x⁴﹣2x²﹣400x=9999的解是

查看试题解析
14. 通过配方，把方程2x²-4x-4=0转化成(x+m)²=a形式为.

查看试题解析
15. 方程 $\sqrt{2} x^{2} - \sqrt{3} x - 1 = 0$ 的解为．

查看试题解析
16. 若一元二次方程ax²=b（ab>0）的两个根分别是m+1与2m－4，则 =.

查看试题解析
17. 已知关于x的一元二次方程mx²﹣（m+2）x+2=0有两个不相等的实数根x₁ ， x₂ ，若x₂＜0，且 $\frac{x_{1}}{x_{2}}$ ＞﹣1，则整数m的值为．

查看试题解析
18. 对于实数a，b，定义运算“﹡”：a﹡b= ${\begin{matrix} a^{2} - a b (a \geq b) \\ a b - b^{2} (a < b) \end{matrix}$ ，例如4﹡2，因为4＞2，所以4﹡2=4²﹣4×2=8．若x₁ ， x₂是一元二次方程x²﹣5x+6=0的两个根，则x₁﹡x₂= ．

查看试题解析

三、解答题

19. 解方程：

(1)、x²﹣4x+1=0．

(2)、（2x-3）²=3(2x-3)

查看试题解析
20. 用适当的方法解下列方程：

(1)、 $4 {(x － 1)}^{2} ＝ 100$

(2)、 $x^{2} - 2 x - 15 = 0$

(3)、 $3 x^{2} － 13 x － 10 ＝ 0$

(4)、 $3 {(x － 3)}^{2} ＋ x （ x － 3) ＝ 0$

查看试题解析
21. 用配方法解关于x的一元二次方程ax²+bx+c=0．

查看试题解析
22. 已知：关于x的一元二次方程x²-3x-k=0有两个不相等的实数根．

(1)、求k的取值范围；

(2)、请选择一个k的负整数值，并求出方程的根．

查看试题解析
23. 对于实数m、n，我们定义一种运算“※”为：m※n=mn+m+n．

(1)、化简：(a+b)※(a一b)；

(2)、解关于x的方程：x※(1※x)=-1．

查看试题解析
24. 在实数范围内定义一种新运算“#”，其规则时：a#b=a²﹣b² ．

(1)、求4#3与（﹣1）#（﹣2）的值；

(2)、求（x+2）#5=0中的x值．

查看试题解析
25. 阅读下列材料：求函数 $y = \frac{3 x^{2} + 2 x}{x^{2} + x + 0.25}$ 的最大值.
解：将原函数转化成关于的一元二次方程，得 $(y - 3) x^{2} - (y - 2) x + \frac{1}{4} y = 0$ .
当 $y \neq 3$ 时，∵x为实数，∴△＝ ${(y - 2)}^{2} - 4 (y - 3) \times \frac{1}{4} y = - y + 4 \geq 0$
∴ $y \leq 4$ 且 $y \neq 3$ ；
当 $y = 3$ 时，即为 $x + \frac{3}{4} = 0$ ，方程有解（ $x$ 的值存在）；
∴ $y \leq 4$ .因此，的最大值为4.
根据材料给你的启示，求函数 $y = \frac{3 x^{2} + x + 2}{x^{2} + 2 x + 1}$ 的最小值.

查看试题解析

2018-2019学年初中数学浙教版八年级下册2.2 一元二次方程的解法 同步练习

一、单选题

二、填空题

三、解答题

2018-2019学年初中数学浙教版八年级下册2.2 一元二次方程的解法同步练习