2016-2017学年广西防城港市九年级上学期期中数学试卷

试卷更新日期：2017-04-12 类型：期中考试

进入出卷网下载

一、选择题

1. 下列方程中，一元二次方程有（）
①3x²+x=20；②2x²﹣3xy+4=0；③ $x^{2} - \frac{1}{x} = 4$ ；④x²=1；⑤ $x^{2} - \frac{x}{3} + 3 = 0$

A、2个 B、3个 C、4个 D、5个

查看试题解析
2. 下列那些数是方程x²+x﹣6=0的根是（）

A、﹣3和2 B、﹣3和﹣2 C、﹣2和3 D、2和3

查看试题解析
3. 用配方法解一元二次方程x²﹣2x﹣5=0，下列配方正确的是（）

A、（x+1）²=6 B、（x+1）²=9 C、（x﹣1）²=6 D、（x﹣1）²=9

查看试题解析
4. 二次函数y=x²+bx+1的对称轴是直线x=﹣3，则b的值是（）

A、4 B、5 C、6 D、7

查看试题解析
5. 抛物线y=﹣x²向右平移1个单位，再向上平移2个单位得到（）

A、y=﹣（x﹣1）²+2 B、y=﹣（x+1）²+2 C、y=﹣（x﹣1）²﹣2 D、y=﹣（x+1）²﹣2

查看试题解析
6. 如图，将△ABC绕点A逆时针旋转一定角度，得到△ADE．若∠CAE=65°，∠E=70°，且AD⊥BC，∠BAC的度数为（）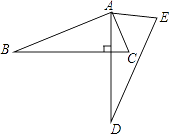

A、60° B、75° C、85° D、90°

查看试题解析
7. 某校计划修建一座既是中心对称图形又是轴对称图形的花坛，从学生中征集到设计方案有等腰三角形，正三角形，等腰梯形和菱形四种图形，你认为符合条件的是（）

A、等腰三角形 B、正三角形 C、等腰梯形 D、菱形

查看试题解析
8. 方程x²﹣9x+18=0的两个根是等腰三角形的底和腰，则这个三角形的周长为（）

A、12 B、15 C、12或15 D、不能确定

查看试题解析
9. 在抛物线y=x²﹣4x+4上的一个点是（）

A、（4，4） B、（3，﹣1） C、（﹣3，﹣1） D、（﹣ $\frac{1}{2}$ ，﹣ $\frac{7}{4}$ ）

查看试题解析
10.
已知函数y=kx+b的图象如图所示，则一元二次方程x²+x+k﹣1=0根的存在情况是（　　）

A、没有实数根 B、有两个相等的实数根 C、有两个不相等的实数根 D、无法确定

查看试题解析
11. 二次函数y=ax²+bx+c（a≠0）的图象如图所示，则点M（a，b+c）在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
12.
如图，Rt△OAB的顶点A（﹣2，4）在抛物线y=ax²上，将Rt△OAB绕点O顺时针旋转90°，得到△OCD，边CD与该抛物线交于点P，则点P的坐标为（）

A、（ $\sqrt{2}$ ， $\sqrt{2}$ ） B、（2，2） C、（ $\sqrt{2}$ ，2） D、（2， $\sqrt{2}$ ）

查看试题解析

二、填空题

13. 方程x（x﹣2）+3（x﹣2）=0的解是．

查看试题解析
14. 已知方程x²﹣5x+15=k²的一个根是2，则另一个根是．

查看试题解析
15. 已知函数y=﹣2x²+x﹣4，当x时，y随x增大而减少．

查看试题解析
16. 某抛物线的顶点坐标为（﹣2，﹣1），开口方向、形状与抛物线y=3x²相同，则此抛物线的解析式是．

查看试题解析
17. 如图，四边形ABCD是菱形，O是两条对角线的交点，过O点的三条直线将菱形分成阴影和空白部分．当菱形的两条对角线的长分别为6和8时，则阴影部分的面积为．

查看试题解析
18. 如图，在△ABC中，∠CAB=65°，将△ABC在平面内绕点A旋转到△AB′C′的位置，使CC′∥AB，则旋转角的度数为度．

查看试题解析

三、解答题

19. 用适当的方法解方程：x²﹣6x+9=（5﹣2x）² ．

查看试题解析
20. 阅读下面的材料，回答问题：
解方程x⁴﹣5x²+4=0，这是一个一元四次方程，根据该方程的特点，它的解法通常是：
设x²=y，那么x⁴=y² ，于是原方程可变为y²﹣5y+4=0 ①，解得y₁=1，y₂=4．
当y=1时，x²=1，∴x=±1；
当y=4时，x²=4，∴x=±2；
∴原方程有四个根：x₁=1，x₂=﹣1，x₃=2，x₄=﹣2．
请你按照上述解题思想解方程（x²+x）²﹣4（x²+x）﹣12=0．

查看试题解析
21. 如图，用一段长为20m的篱笆围成一个一边靠墙的矩形菜园，墙长为18m．这个矩形的长、宽各是多少时，菜园面积最大？最大面积是多少？

查看试题解析
22. 如图1，在△ABC和△EDC中，AC=CE=CB=CD；∠ACB=∠DCE=90°，AB与CE交于F，ED与AB，BC，分别交于M，H．

(1)、求证：CF=CH；

(2)、如图2，△ABC不动，将△EDC绕点C旋转到∠BCE=45°时，试判断四边形ACDM是什么四边形？并证明你的结论．

查看试题解析
23. 某商场销售一批名牌衬衫，平均每天可售出20件，每件赢利40元，为了扩大销售，增加利润，尽量减少库存，商场决定采取适当的降价措施．经调查发现，如果每件衬衫每降价1元，商场平均每天可多售出2件；

(1)、若商场平均每天要赢利1200元，每件衬衫应降价多少元？

(2)、每件衬衫降价多少元时，商场平均每天赢利最多？

查看试题解析
24. 如图，抛物线y=x²+bx+c与x轴交于A（﹣1，0），B（3，0）两点．

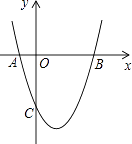(1)、求该抛物线的解析式；

(2)、求该抛物线的对称轴以及顶点坐标；

(3)、设（1）中的抛物线上有一个动点P，当点P在该抛物线上滑动到什么位置时，满足S_△_PAB=8，并求出此时P点的坐标．

查看试题解析
25. 如图，A、B、C、D为矩形的四个顶点，AB=16cm，AD=6cm，动点P、Q分别从点A、C同时出发，点P以3cm/s的速度向点B移动，一直到达B为止，点Q以2 cm/s的速度向D移动．

(1)、P、Q两点从出发开始到几秒？四边形PBCQ的面积为33cm²；

(2)、P、Q两点从出发开始到几秒时？点P和点Q的距离是10cm．

查看试题解析
26. 在平面直角坐标系中，已知抛物线经过A（﹣4，0），B（0，﹣4），C（2，0）三点．

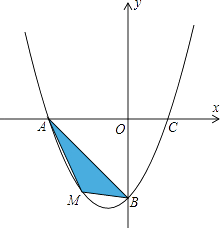(1)、求抛物线的解析式；

(2)、若点M为第三象限内抛物线上一动点，点M的横坐标为m，△AMB的面积为S．
求S关于m的函数关系式，并求出S的最大值．

(3)、若点P是抛物线上的动点，点Q是直线y=﹣x上的动点，判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形，直接写出相应的点Q的坐标．

查看试题解析