2016-2017学年广东省肇庆市封开县九年级上学期期中数学试卷
试卷更新日期：2017-04-12 类型：期中考试
一、选择题
-
1. 下列方程中，属于一元二次方程的是（ ）A、x2﹣ =1 B、x2+y=2 C、 x2=2 D、x+5=﹣72. 下列安全标志图中，是中心对称图形的是（ ）A、
B、
C、
D、
3. 抛物线y=﹣2x2﹣3与y轴交点的纵坐标为（ ）A、﹣3 B、﹣4 C、﹣5 D、﹣14. 在平面直角坐标系中，点A（﹣2，1）与点B关于原点对称，则点B的坐标为（ ）A、（﹣2，1） B、（2，﹣1） C、（2，1） D、（﹣2，﹣1）5. 方程（x﹣2）（x+3）=0的解是（ ）A、x=2 B、x=﹣3 C、x1=2，x2=3 D、x1=2，x2=﹣36. 已知二次函数y=2x2﹣7x+3，若y随x的增大而增大，则x的取值范围是（ ）A、x＞ B、x＜ C、x＜﹣ D、x＞﹣7. 若关于x的一元二次方程方程（k﹣1）x2+4x+1=0有实数根，则k的取值范围是（ ）A、k＜5 B、k≥5，且k≠1 C、k≤5，且k≠1 D、k＞58. 已知x=2是关于x的方程 的一个解，则2a﹣1的值是（ ）A、3 B、4 C、5 D、69. 在平面直角坐标系中，把点P（﹣5，3）向右平移8个单位得到点P1 ， 再将点P1绕原点旋转90°得到点P2 ， 则点P2的坐标是（ ）A、（3，﹣3） B、（﹣3，3） C、（3，3）或（﹣3，﹣3） D、（3，﹣3）或（﹣3，3）10. 一次函数y=ax+b（a≠0）与二次函数y=ax2+bx+c（a≠0）在同一平面直角坐标系中的图象可能是（ ）A、
B、
C、
D、
二、填空题
-
11. 时针6点到9点，时针转动了度．12. 抛物线y=﹣3（x﹣1）2+5的顶点坐标为 ．13. 方程（3x+1）（2x﹣3）=1化成一般式的常数项是 ．14. 已知m＜0，则点P（m2 ， ﹣m+3）关于原点的对称点Q在第象限．15. 若（m+1）xm（m+2）﹣1+2m﹣1=0是关于x的一元二次方程，则m的值是 ．16. 如图，在长为10cm，宽为8cm的矩形的四个角上截去四个全等的小正方形，使得留下的图形（图中阴影部分）面积是原矩形面积的80%，则所截去小正方形的边长是 cm．
三、解答题。
-
17. 解方程：x2﹣4x﹣5=018. 每个小方格都是边长为1个单位长度的正方形，在建立平面直角坐标系后，△ABC的顶点均在格点上，
①写出A、B、C的坐标．
②以原点O为对称中心，画出△ABC关于原点O对称的△A1B1C1 ， 并写出A1、B1、C1 ．
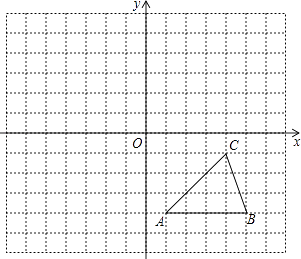19. 一辆汽车的行驶距离s（单位：m）关于行驶时间t（单位：s）的函数解析式是s=9t+ t2 ， 经过12s汽车行驶了多远？行驶380m需要多少时间？20. 已知关于x的二次函数y=x2﹣6x+2m﹣1，(1)、当m为何值时，函数与x轴没有交点；(2)、当m=﹣3时，求二次函数与坐标轴的交点坐标．21. 如图，在平面直角坐标系中，如图所示，△AOB是边长为2的等边三角形，将△AOB绕着点B按顺时针方向旋转得到△DCB，使得点D落在x轴的正半轴上，连接OC、AD．
(1)、求证：OC=AD；(2)、求OC的长．22. 两年前生产1吨甲种药品的成本是5000元，生产1吨乙种药品的成本是6000元，随着生产技术的进步，现在生产1吨甲种药品的成本是4050元，生产1吨乙种药品的成本是4860元，哪种药品成本的年平均下降率较大？23. 如图，在△ABC和△EDC中，AC=CE=CB=CD；∠ACB=∠DCE=90°，AB与CE交于F，ED与AB，BC，分别交于M，H．
(1)、求证：CF=CH；(2)、△ABC不动，将△EDC绕点C旋转到∠BCE=45°，证明：四边形ACDM是菱形．24. 某中学课外兴趣活动小组准备围建一个矩形苗圃园，其中一边靠墙，另外三边由长为30米的篱笆围成．已知墙长为18米（如图所示），设这个苗圃园垂直于墙的一边长为x米．
(1)、若苗圃园的面积为72平方米，求x；(2)、若平行于墙的一边长不小于8米，这个苗圃园的面积有最大值和最小值吗？如果有，求出最大值和最小值；如果没有，请说明理由．25. 如图，抛物线y=x2+bx+c与x轴交于A（﹣1，0），B（3，0）两点．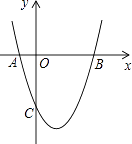
(1)、求该抛物线的解析式；(2)、求该抛物线的对称轴以及顶点坐标；(3)、设（1）中的抛物线上有一个动点P，当点P在该抛物线上滑动到什么位置时，满足S△PAB=8，并求出此时P点的坐标．