2016-2017学年福建省漳州市龙海市石码片九年级上学期期中数学试卷
试卷更新日期:2017-04-12 类型:期中考试
一、选择题
-
1. 二次根式 与 + 的关系是( )A、互为相反数 B、互为倒数 C、互为有理化因式 D、相等2. 如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与△ABC相似的是( )
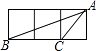 A、
A、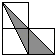 B、
B、 C、
C、 D、
D、 3. 下列根式中,是最简二次根式的有( )
3. 下列根式中,是最简二次根式的有( )① ;② ;③ ;④ ;⑤ ;⑥ .
A、②③⑤ B、②③⑥ C、②③④⑥ D、①③⑤⑥4. 若一元二次方程x2﹣2x﹣m=0无实数根,则一次函数y=(m+1)x+m﹣1的图象不经过第( )象限.A、四 B、三 C、二 D、一5. 化简a 的结果是( )A、 B、 C、 D、6. 定义运算:a⋆b=a(1﹣b).若a,b是方程x2﹣x+ m=0(m<0)的两根,则b⋆b﹣a⋆a的值为( )A、0 B、1 C、2 D、与m有关7. 如图,D是△ABC的边BC上任一点,已知AB=6,AD=3,∠DAC=∠B.若△ABD的面积为a,则△ACD的面积为( )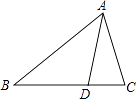 A、a B、 C、 D、 a8. 如图,在△ABC中,BF平分∠ABC,AF⊥BF于点F,D为AB的中点,连接DF延长交AC于点E.若AB=10,BC=16,则线段EF的长为( )
A、a B、 C、 D、 a8. 如图,在△ABC中,BF平分∠ABC,AF⊥BF于点F,D为AB的中点,连接DF延长交AC于点E.若AB=10,BC=16,则线段EF的长为( ) A、2 B、3 C、4 D、59. 如图,在平面直角坐标中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为 ,点A,B,E在x轴上,若正方形BEFG的边长为6,则C点坐标为( )
A、2 B、3 C、4 D、59. 如图,在平面直角坐标中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为 ,点A,B,E在x轴上,若正方形BEFG的边长为6,则C点坐标为( )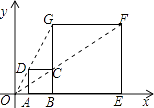 A、(3,2) B、(3,1) C、(2,2) D、(4,2)10.
A、(3,2) B、(3,1) C、(2,2) D、(4,2)10.在一幅长80cm,宽50cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是5400cm2 , 设金色纸边的宽为xcm,那么x满足的方程是( )
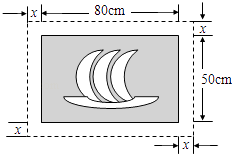 A、x2+130x﹣1400=0 B、x2+65x﹣350=0 C、x2﹣130x﹣1400=0 D、x2﹣65x﹣350=0
A、x2+130x﹣1400=0 B、x2+65x﹣350=0 C、x2﹣130x﹣1400=0 D、x2﹣65x﹣350=0二、填空题
-
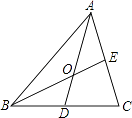
11. 如图,AD、BE是△ABC的中线,且相交于点O,已知AD=7.5cm,则DO=cm.
 12. 已知关于x的一元二次方程(a﹣2)x2+x+a2﹣4=0的一个根是0,则a的值为 .13. 如果 = • 成立,则x的取值范围是 .14. 设一元二次方程x2﹣3x﹣1=0的两根分别是x1 , x2 , 则x1+x2(x22﹣3x2)= .15. 晚上,小亮走在大街上.他发现:当他站在大街两边的两盏路灯之间,并且自己被两边路灯照在地上的两个影子成一直线时,自己右边的影子长为3米,左边的影子长为1.5米.又知自己身高1.80米,两盏路灯的高相同,两盏路灯之间的距离为12米,则路灯的高为米.
12. 已知关于x的一元二次方程(a﹣2)x2+x+a2﹣4=0的一个根是0,则a的值为 .13. 如果 = • 成立,则x的取值范围是 .14. 设一元二次方程x2﹣3x﹣1=0的两根分别是x1 , x2 , 则x1+x2(x22﹣3x2)= .15. 晚上,小亮走在大街上.他发现:当他站在大街两边的两盏路灯之间,并且自己被两边路灯照在地上的两个影子成一直线时,自己右边的影子长为3米,左边的影子长为1.5米.又知自己身高1.80米,两盏路灯的高相同,两盏路灯之间的距离为12米,则路灯的高为米. 16. 如图所示,在△ABC中,AB=8cm,BC=16cm.点P从点A出发沿AB向点B以2cm/s的速度运动,点Q从点B出发沿BC向点C以4cm/s的速度运动.如果点P,Q分别从点A,B同时出发,则秒钟后△PBQ与△ABC相似?
16. 如图所示,在△ABC中,AB=8cm,BC=16cm.点P从点A出发沿AB向点B以2cm/s的速度运动,点Q从点B出发沿BC向点C以4cm/s的速度运动.如果点P,Q分别从点A,B同时出发,则秒钟后△PBQ与△ABC相似?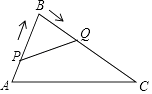
三、解答题
-
17. 计算 ﹣(π﹣3)0+(﹣ )﹣1﹣ +| ﹣2|.18. 解方程 (3x﹣1)2=(x﹣1)2 .19. 如图,点C 把线段 AB 分成两条线段 AC 和 BC,如果满足 ,那么我们称点C是线段 AB的黄金分割点,若AB=1,求AC的长.
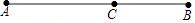 20. 若a,b为实数,且b= ,(1)、求 的值;(2)、若 的值是关于x的一元二次方程x2﹣2x+k2+k=0的一个根;求k及另一个根.21.
20. 若a,b为实数,且b= ,(1)、求 的值;(2)、若 的值是关于x的一元二次方程x2﹣2x+k2+k=0的一个根;求k及另一个根.21.如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,﹣1).
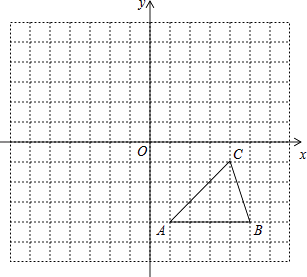 (1)、把△ABC向上平移5个单位后得到对应的△A1B1C1 , 画出△A1B1C1 , 并写出C1的坐标.(2)、以点B为位似中心在格纸内画出△A2BC2 , 且与△ABC的位似比为2:1,并写出C2的坐标.22. 已知:如图,在四边形ABCD中,AD∥BC,∠C=90°,AB=AD=50,BC=64,连结BD,AE⊥BD垂足为E,
(1)、把△ABC向上平移5个单位后得到对应的△A1B1C1 , 画出△A1B1C1 , 并写出C1的坐标.(2)、以点B为位似中心在格纸内画出△A2BC2 , 且与△ABC的位似比为2:1,并写出C2的坐标.22. 已知:如图,在四边形ABCD中,AD∥BC,∠C=90°,AB=AD=50,BC=64,连结BD,AE⊥BD垂足为E,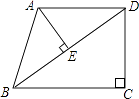 (1)、求证:△ABE∽△DCB;(2)、求线段DC的长.23. 某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利40元,为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出5件.(1)、若商场平均每天要盈利2400元,每件衬衫应降价多少元?(2)、若该商场要每天盈利最大,每件衬衫应降价多少元?盈利最大是多少元?24. 如图①,先把一矩形ABCD纸片上下对折,设折痕为MN;如图②,再把点B 叠在折痕线MN上,得到Rt△ABE.过B点作PQ⊥AD,分别交BC、AD于点P、Q.
(1)、求证:△ABE∽△DCB;(2)、求线段DC的长.23. 某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利40元,为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出5件.(1)、若商场平均每天要盈利2400元,每件衬衫应降价多少元?(2)、若该商场要每天盈利最大,每件衬衫应降价多少元?盈利最大是多少元?24. 如图①,先把一矩形ABCD纸片上下对折,设折痕为MN;如图②,再把点B 叠在折痕线MN上,得到Rt△ABE.过B点作PQ⊥AD,分别交BC、AD于点P、Q.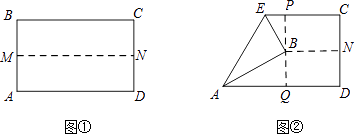 (1)、求证:△PBE∽△QAB;(2)、在图②中,EB是否平分∠AEC?请说明理由;(3)、在(1)(2)的条件下,若AB=4,求PE的长度.25. 如图所示,在平面直角坐标系中,过点A(﹣ ,0)的两条直线分别交y轴于B、C两点,且B、C两点的纵坐标分别是一元二次方程x2﹣2x﹣3=0的两个根
(1)、求证:△PBE∽△QAB;(2)、在图②中,EB是否平分∠AEC?请说明理由;(3)、在(1)(2)的条件下,若AB=4,求PE的长度.25. 如图所示,在平面直角坐标系中,过点A(﹣ ,0)的两条直线分别交y轴于B、C两点,且B、C两点的纵坐标分别是一元二次方程x2﹣2x﹣3=0的两个根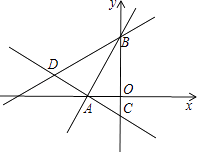 (1)、求线段BC的长度;(2)、试问:直线AC与直线AB是否垂直?请说明理由;(3)、若点D在直线AC上,且DB=DC,求直线BD的解析式;(4)、在x轴上是否存在P,使以O、B、P三点为顶点的三角形与△ABC相似?若存在,请直接写出P点的坐标;若不存在,请说明理由.
(1)、求线段BC的长度;(2)、试问:直线AC与直线AB是否垂直?请说明理由;(3)、若点D在直线AC上,且DB=DC,求直线BD的解析式;(4)、在x轴上是否存在P,使以O、B、P三点为顶点的三角形与△ABC相似?若存在,请直接写出P点的坐标;若不存在,请说明理由.