2016-2017学年福建省莆田市仙游县郊尾、枫亭五校教研小片区九年级上学期期中数学试卷

试卷更新日期：2017-04-12 类型：期中考试

进入 出卷网 下载

一、选择题

  • 1. 下列图形中国，是中心对称图形的是（   ）

    A、    B、    C、    D、

    查看试题解析

  • 2. 下列诗句所描述的事件中，是不可能事件的是（   ）
    A、黄河入海流 B、锄禾日当午 C、大漠孤烟直 D、手可摘星辰

    查看试题解析

  • 3. 点B与点A（﹣2，3）关于原点对称，点B的坐标为（   ）
    A、（2，﹣3） B、（﹣2，3） C、（2，3） D、（﹣2，﹣3）

    查看试题解析

  • 4. 抛物线y=（x+2）2﹣3可以由抛物线y=x2平移得到，则下列平移过程正确的是（   ）
    A、先向左平移2个单位，再向上平移3个单位 B、先向左平移2个单位，再向下平移3个单位 C、先向右平移2个单位，再向下平移3个单位 D、先向右平移2个单位，再向上平移3个单位

    查看试题解析

  • 5. 如图，⊙O是△ABC的外接圆，连接OA、OB，∠OBA=50°，则∠C的度数为（   ）

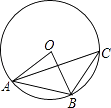    A、30° B、40° C、50° D、80°

    查看试题解析

  • 6. 如图，在方格纸中，随机选择标有序号①②③④⑤中的一个小正方形涂黑，与图中阴影部分构成轴对称图形的概率是（   ）

    A、15 B、25 C、35 D、45

    查看试题解析

  • 7. 已知⊙O的半径为3，圆心O到直线L的距离为2，则直线L与⊙O的位置关系是（   ）
    A、不能确定 B、相离 C、相切 D、相交

    查看试题解析

  • 8. 用反证法证明命题“三角形中必有一个内角小于或等于60°”时，首先应假设这个三角形中（   ）
    A、每一个内角都大于60° B、每一个内角都小于60° C、有一个内角大于60° D、有一个内角小于60°

    查看试题解析

  • 9. 如图，一个宽为2 cm的刻度尺在圆上移动，当刻度尺的一边与圆相切时，另一边与圆两个交点处的读数恰好为“2”和“8”（单位：cm），那么该圆的半径为（   ）

    A、13 cm B、2516 cm C、3cm D、134 cm

    查看试题解析

  • 10. 已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，给出以下结论：①abc＜0；②2a+b=0；③当x=﹣1或x=3时，函数y的值都等于0；④4a+2b+c＞0，其中正确结论的个数是（   ）

    A、1个 B、2个 C、3个 D、4个

    查看试题解析

二、填空题

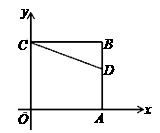
  • 11. 抛物线y=2（x﹣1）2+5的顶点坐标是 ．

    查看试题解析

  • 12. 函数 y=(m−1)xm2+1−2mx+1 的图象是抛物线，则m= ．

    查看试题解析

  • 13. 已知圆锥的底面半径是2，母线长是4，则圆锥的侧面积是 ．

    查看试题解析

  • 14. 关于x的一元二次方程（a﹣5）x2﹣4x﹣1=0有实数根，则实数a的取值范围是 ．

    查看试题解析

  • 15. 如图，正方形OABC的两边OA、OC分别在x轴、y轴上，点D（5，3）在边AB上，以C为中心，把△CDB旋转90°，则旋转后点D的对应点D′的坐标是。

    查看试题解析

  • 16. 如图，Rt△ABC中，∠C=90°，若AC=4，BC=3，则△ABC的内切圆半径r= ．

    查看试题解析

三、解答题

  • 17. 解下列方程

    (1)、x2+x﹣1=0

    (2)、x（x﹣2）+x﹣2=0．

    查看试题解析

  • 18.

    如图4×4的正方形网格中，将△MNP绕某点旋转一定的角度，得到△M1N1P1 ， 试用尺规作图法确定旋转中心A点（保留作图痕迹，标出A点）

    查看试题解析

  • 19. 一只不透明袋子中装有1个红球，2个黄球，这些球除颜色外都相同，小明搅匀后从中任意摸出一个球，记录颜色后放回、搅匀，再从中任意摸出1个球，用树状图或列表法列出摸出球的所有等可能情况，并求两次摸出的球都是黄色的概率．

    查看试题解析

  • 20. 如图，AD，BC是⊙O的两条弦，且AD=BC，求证：AB=CD．

    查看试题解析

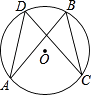  • 21. 某小区规划在一块长32米，宽20米的矩形场地修建三条同样宽的小路，使其中两条平行，另一条与之垂直，其余部分种草，草坪的面积为570米2 ， 小路的宽度应是多少？

    查看试题解析

  • 22. 在直角坐标平面内，点 O为坐标原点，二次函数 y=x2+（k﹣5）x﹣（k+4）的图象交 x轴于点A（x1 ， 0）、B（x2 ， 0），且（x1+1）（x2+1）=﹣8．求二次函数解析式．

    查看试题解析

  • 23. 如图，在△ABC中，AB=AC，以AB为直径的⊙O交BC于点M，MN⊥AC于点N．

    求证：MN是⊙O的切线．

    查看试题解析

  • 24. 如图，正方形ABCD中，E为CD上一点，F为BC延长线上一点，CE=CF．

    (1)、△DCF可以看做是△BCE绕点C旋转某个角度得到的吗？说明理由．
    (2)、若∠CEB=60°，求∠EFD的度数．

    查看试题解析

  • 25. 为了响应政府提出的由中国制造向中国创造转型的号召，某公司自主设计了一款成本为40元的可控温杯，并投放市场进行试销售，经过调查发现该产品每天的销售量y（件）与销售单价x（元）满足一次函数关系：y=﹣10x+1200．
    (1)、求出利润S（元）与销售单价x（元）之间的关系式（利润=销售额﹣成本）；
    (2)、当销售单价定为多少时，该公司每天获取的利润最大？最大利润是多少元？

    查看试题解析

  • 26.

    已知二次函数y=x2+bx+c的图象过点A（﹣3，0）和点B（1，0），且与y轴交于点C，D点在抛物线上且横坐标是﹣2．

    (1)、求抛物线的解析式；

    (2)、抛物线的对称轴上有一动点P，求出PA+PD的最小值．

    查看试题解析