天津市南开区2018-2019学年八年级上学期数学期中考试试卷
试卷更新日期:2019-01-16 类型:期中考试
一、选择题
-
1. 如图图案是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如图,若AB=AD,则添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
2. 如图,若AB=AD,则添加下列一个条件后,仍无法判定△ABC≌△ADC的是( ) A、
A、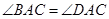 B、
B、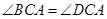 C、
C、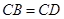 D、
D、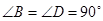 3. 下列运算正确的是( )A、
3. 下列运算正确的是( )A、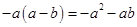 B、
B、 C、
C、 D、
D、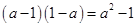 4. 在下列说法中,正确的是( )
4. 在下列说法中,正确的是( )
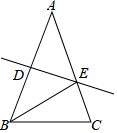
A、如果两个三角形全等,则它们必是关于直线成轴对称的图形 B、如果两个三角形关于某直线成轴对称,那么它们是全等三角形 C、等腰三角形是关于底边中线成轴对称的图形 D、一条线段是关于经过该线段中点的直线成轴对称的图形5. 如图AB=CD,AD=BC,过O点的直线交AD于E,交BC于F,图中全等三角形有( )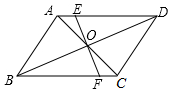 A、4对 B、5对 C、6对 D、7对6. 如图,Rt△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边CB上A′处,折痕为CD,则∠A′DB=( )
A、4对 B、5对 C、6对 D、7对6. 如图,Rt△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边CB上A′处,折痕为CD,则∠A′DB=( )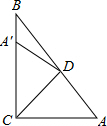 A、
A、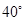 B、
B、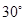 C、
C、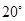 D、
D、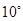 7. 计算( )2003×1.52002×(-1)2004的结果是( )A、 B、 C、
7. 计算( )2003×1.52002×(-1)2004的结果是( )A、 B、 C、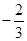 D、
D、 8. 如图所示,有两个长度相同的滑梯(即BC=EF),左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,则下列结论:(1)AB=DE;(2)∠ABC+∠DFE=90°;(3)∠ABC=∠DEF中正确的有( )
8. 如图所示,有两个长度相同的滑梯(即BC=EF),左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,则下列结论:(1)AB=DE;(2)∠ABC+∠DFE=90°;(3)∠ABC=∠DEF中正确的有( )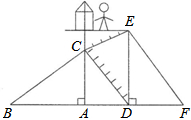 A、1个 B、2个 C、3个 D、0个9. 如果x2+6x+k2恰好是一个整式的平方,那么常数k的值为( )A、3 B、 C、
A、1个 B、2个 C、3个 D、0个9. 如果x2+6x+k2恰好是一个整式的平方,那么常数k的值为( )A、3 B、 C、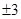 D、9
10. 如图,△ABC的三边AB,BC,CA长分别是20,30,40,其三条角平分线将△ABC分为三个三角形,则S△ABO:S△BCO:S△CAO等于( )
D、9
10. 如图,△ABC的三边AB,BC,CA长分别是20,30,40,其三条角平分线将△ABC分为三个三角形,则S△ABO:S△BCO:S△CAO等于( )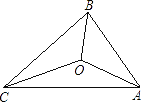 A、1:1:1 B、1:2:3 C、2:3:4 D、3:4:511. 如图,已知∠ACB=60°,PC=12,点M,N在边CB上,PM=PN.若MN=3,则CM的长为( )
A、1:1:1 B、1:2:3 C、2:3:4 D、3:4:511. 如图,已知∠ACB=60°,PC=12,点M,N在边CB上,PM=PN.若MN=3,则CM的长为( )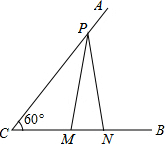 A、3 B、
A、3 B、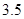 C、4
D、
C、4
D、 12. 如图,△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,DH⊥BC于H,交BE于G,下列结论:①BD=CD;②AD+CF=BD;③CE= BF;④AE=BG.其中正确的是( )
12. 如图,△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,DH⊥BC于H,交BE于G,下列结论:①BD=CD;②AD+CF=BD;③CE= BF;④AE=BG.其中正确的是( )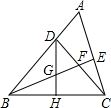 A、
A、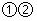 B、
B、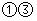 C、
C、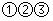 D、
D、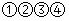
二、填空题
-
13. 若点P(a+2,3)与点Q(-1,b+1)关于y轴对称,则ab= .14. 计算:20182-2017×2019= .15. 如图,在△ABC中,AB=AC=10,△BEC的周长是17,DE垂直平分AB,交AB于点D,交AC于点E,则BC= .
 16. 在平面直角坐标系中,已知点A(1,2),B(5,5),C(5,2),存在点E,使△ACE和△ACB全等,写出所有满足条件的E点的坐标 .17. 如图,△ABC是边长为3的等边三角形,△BDC是等腰三角形,且∠BDC=120°.以D为顶点作一个60°角,使其两边分别交AB于点M,交AC于点N,连接MN,则△AMN的周长为 .
16. 在平面直角坐标系中,已知点A(1,2),B(5,5),C(5,2),存在点E,使△ACE和△ACB全等,写出所有满足条件的E点的坐标 .17. 如图,△ABC是边长为3的等边三角形,△BDC是等腰三角形,且∠BDC=120°.以D为顶点作一个60°角,使其两边分别交AB于点M,交AC于点N,连接MN,则△AMN的周长为 .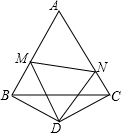 18. 已知:如图,△ABC是边长3cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止当t=时,△PBQ是直角三角形.
18. 已知:如图,△ABC是边长3cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止当t=时,△PBQ是直角三角形.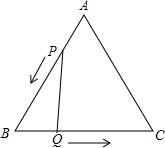
三、计算题
-
19. 计算:(1)、(3x2y)2•(-15xy3)÷(-9x4y2)(2)、(2a-3)2-(1-a)2(3)、先化简,再求值:(2+x)(2-x)+(x-1)(x+5),其中x= .20. 如图,平面直角坐标系中,点A、B分别在x、y轴上,点B的坐标为(0,1),∠BAO=30°.
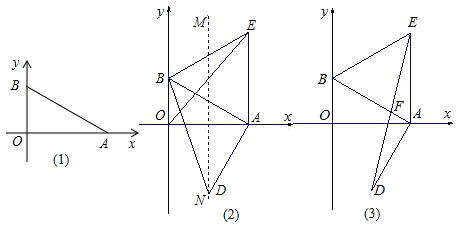 (1)、求AB的长度;(2)、以AB为一边作等边△ABE,作OA的垂直平分线MN交AB的垂线AD于点D.求证:BD=OE;(3)、在(2)的条件下,连接DE交AB于F.求证:F为DE的中点.
(1)、求AB的长度;(2)、以AB为一边作等边△ABE,作OA的垂直平分线MN交AB的垂线AD于点D.求证:BD=OE;(3)、在(2)的条件下,连接DE交AB于F.求证:F为DE的中点.四、解答题
-
21. 如图,在平面直角坐标系中,A(-3,2),B(-4,-3),C(-1,-1).
 (1)、在图中作出△ABC关于y轴对称的△A1B1C1;(2)、写出点C1的坐标(直接写答案):C1;(3)、△A1B1C1的面积为;(4)、在y轴上画出点P,使PB+PC最小.22. 我们把两组邻边相等的四边形叫做“筝形”.如图,四边形ABCD是一个筝形,其中AB=CB,AD=CD.对角线AC,BD相交于点O,OE⊥AB,OF⊥CB,垂足分别是E,F.求证OE=OF.
(1)、在图中作出△ABC关于y轴对称的△A1B1C1;(2)、写出点C1的坐标(直接写答案):C1;(3)、△A1B1C1的面积为;(4)、在y轴上画出点P,使PB+PC最小.22. 我们把两组邻边相等的四边形叫做“筝形”.如图,四边形ABCD是一个筝形,其中AB=CB,AD=CD.对角线AC,BD相交于点O,OE⊥AB,OF⊥CB,垂足分别是E,F.求证OE=OF.