天津市河西区2018-2019学年九年级上学期数学期中考试试卷
试卷更新日期:2019-01-16 类型:期中考试
一、选择题
-
1. 下列各点中,在二次函数y=-x2的图象上的是( )A、
 B、
B、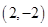 C、
C、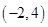 D、
D、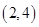 2. 下列图案中,可以看作是中心对称图形的是( )A、
2. 下列图案中,可以看作是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 3. 如图,在⊙O中,弧AB=弧AC,∠A=36°,则∠C的度数为( )
3. 如图,在⊙O中,弧AB=弧AC,∠A=36°,则∠C的度数为( ) A、
A、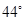 B、
B、 C、
C、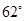 D、
D、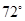 4. 下列二次函数的图象中,其对称轴是x=1的为( )A、
4. 下列二次函数的图象中,其对称轴是x=1的为( )A、 B、
B、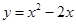 C、
C、 D、
D、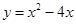 5. 在一个边长为2的正方形中挖去一个边长为x(0<x<2)的小正方形,如果设剩余部分的面积为y,那么y关于x的函数解析式是( )A、
5. 在一个边长为2的正方形中挖去一个边长为x(0<x<2)的小正方形,如果设剩余部分的面积为y,那么y关于x的函数解析式是( )A、 B、
B、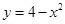 C、
C、 D、
D、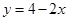 6.
6.如图,⊙O中,弦AB的长为8cm,圆心O到AB的距离为3cm,则⊙O的半径长为( )
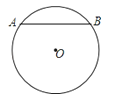 A、3cm B、4cm C、5cm D、6cm7. 方程x2-4x-12=0的解为( )A、
A、3cm B、4cm C、5cm D、6cm7. 方程x2-4x-12=0的解为( )A、 ,
,  B、
B、 ,
,  C、
C、 ,
,  D、
D、 ,
,  8. 若方程x2+9x-a=0有两个相等的实数根,则( )A、
8. 若方程x2+9x-a=0有两个相等的实数根,则( )A、 B、
B、 C、
C、 D、
D、 9. 抛物线y=x2+x+1与两坐标轴的交点个数为( )A、0个 B、1个 C、2个 D、3个10. 如图,将△ABC绕点B顺时针旋转60°得△DBE,点C的对应点E恰好落在AB的延长线上,连接AD.下列结论一定正确的是( )
9. 抛物线y=x2+x+1与两坐标轴的交点个数为( )A、0个 B、1个 C、2个 D、3个10. 如图,将△ABC绕点B顺时针旋转60°得△DBE,点C的对应点E恰好落在AB的延长线上,连接AD.下列结论一定正确的是( ) A、
A、 B、
B、 C、
C、 D、
D、 是等边三角形
11. 如图,在⊙O中,AB、AC为互相垂直且相等的两条弦,则下列说法中正确的有( )
是等边三角形
11. 如图,在⊙O中,AB、AC为互相垂直且相等的两条弦,则下列说法中正确的有( )①点C、O、B一定在一条直线上;②若点E、点D分别是CA、AB的中点,则OE=OD;③若点E是CA的中点,连接CO,则△CEO是等腰直角三角形.
 A、3个 B、2个 C、0个12. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示有下列4个结论:①abc>0;②b<a+c;③4a+2b+c>0;④a+b>m(am+b)(m≠1的实数),其中正确结论的个数为( )
A、3个 B、2个 C、0个12. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示有下列4个结论:①abc>0;②b<a+c;③4a+2b+c>0;④a+b>m(am+b)(m≠1的实数),其中正确结论的个数为( )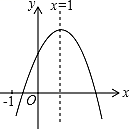 A、0 B、1 C、2 D、3
A、0 B、1 C、2 D、3二、填空题
-
13. 点(-3,5)关于原点对称的点的坐标是 .14. 如图,A、B、C是⊙O上的三点,∠AOB=100°,则∠ACB=度.
 15. 如图,在平面直角坐标系xOy中,四边形OABC是正方形,点C(0,4),D是OA中点,将△CDO以C为旋转中心逆时针旋转90°,写出此时点D的对应点的坐标 .
15. 如图,在平面直角坐标系xOy中,四边形OABC是正方形,点C(0,4),D是OA中点,将△CDO以C为旋转中心逆时针旋转90°,写出此时点D的对应点的坐标 . 16. 将抛物线y=x2向下平移2个单位长度,平移后拋物线的解析式为 .17. 抛物线y=x2-4x-10与x轴的两交点间的距离为 .18. 如图,在Rt△ABC中,∠B=90°,AB=2 ,BC= ,将△ABC绕点A按逆时针方向旋转90°得到△AB′C′,连接B′C,则CB′的长度为 .
16. 将抛物线y=x2向下平移2个单位长度,平移后拋物线的解析式为 .17. 抛物线y=x2-4x-10与x轴的两交点间的距离为 .18. 如图,在Rt△ABC中,∠B=90°,AB=2 ,BC= ,将△ABC绕点A按逆时针方向旋转90°得到△AB′C′,连接B′C,则CB′的长度为 .
三、计算题
-
19. 在平面直角坐标系中,四边形AOBC是矩形,点O(0,0),点A(5,0),点B(0,3),以点A为中心,顺时针旋转矩形AOBC,得到矩形ADEF,点O、B、C的对应点分别为D、E、F,且点D恰好落在BC边上.
 (1)、在原图上画出旋转后的矩形;(2)、求此时点D的坐标.20. 已知,△ABC中,∠A=68°,以AB为直径的⊙O与AC,BC的交点分别为D,E(1)、如图①,求∠CED的大小;(2)、如图②,当DE=BE时,求∠C的大小.
(1)、在原图上画出旋转后的矩形;(2)、求此时点D的坐标.20. 已知,△ABC中,∠A=68°,以AB为直径的⊙O与AC,BC的交点分别为D,E(1)、如图①,求∠CED的大小;(2)、如图②,当DE=BE时,求∠C的大小.四、解答题
-
21. 解方程:x2-4x-5=0.22. 已知:抛物线y=-x2-6x+21.求:(1)、直接写出抛物线y=-x2-6x+21的顶点坐标;(2)、当x>2时,求y的取值范围.23. 某景区商店销售一种纪念品,每件的进货价为40元.经市场调研,当该纪念品每件的销售价为50元时,每天可销售200件;当每件的销售价每增加1元,每天的销售数量将减少10件.(1)、当每件的销售价为52元时,该纪念品每天的销售数量为件;(2)、当每件的销售价x为多少时,销售该纪念品每天获得的利润y最大?并求出最大利润.24. 在平面直角坐标系中,O为原点,点A(4,0),点B(0,3),把△ABO绕点B逆时针旋转得到△A′BO′,点A、O旋转后的对应点为A′、O′,记旋转角为α.
 (1)、如图①,若α=90°,求AA′的长;(2)、如图②,若α=120°,求点O′的坐标;(3)、记K为AB的中点,S为△KA′O′的面积,求S的取值范围(直接写出结果即可).25. 已知抛物线y=x2+bx+c与x轴交于点A(-3,0)、B(1,0),C为顶点,直线y=x+m经过点A,与y轴交于点D.(1)、求b、c的值;(2)、求∠DAO的度数和线段AD的长;(3)、平移该抛物线得到一条新抛物线,设新抛物线的顶点为C′,若新抛物线经过点D,并且新抛物线的顶点和原抛物线的顶点的连线CC′平行于直线AD,求新抛物线对应的函数表达式.
(1)、如图①,若α=90°,求AA′的长;(2)、如图②,若α=120°,求点O′的坐标;(3)、记K为AB的中点,S为△KA′O′的面积,求S的取值范围(直接写出结果即可).25. 已知抛物线y=x2+bx+c与x轴交于点A(-3,0)、B(1,0),C为顶点,直线y=x+m经过点A,与y轴交于点D.(1)、求b、c的值;(2)、求∠DAO的度数和线段AD的长;(3)、平移该抛物线得到一条新抛物线,设新抛物线的顶点为C′,若新抛物线经过点D,并且新抛物线的顶点和原抛物线的顶点的连线CC′平行于直线AD,求新抛物线对应的函数表达式.