四川省自贡市普高2018-2019学年文数第一次诊断性考试试卷
试卷更新日期:2019-01-16 类型:高考模拟
一、单选题
-
1. 已知 , ,则 ( )A、
 B、
B、 或
或  C、
C、 D、
D、 2. 若 (其中 为虚数单位),则复数 的虚部是( )A、
2. 若 (其中 为虚数单位),则复数 的虚部是( )A、 B、
B、 C、
C、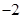 D、2
3. 等差数列 的前 项和为 ,若 ,则 ( )A、66 B、99 C、110 D、1434. 若 ,则 ( )A、
D、2
3. 等差数列 的前 项和为 ,若 ,则 ( )A、66 B、99 C、110 D、1434. 若 ,则 ( )A、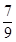 B、
B、 C、
D、
C、
D、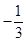 5. 在矩形 中, , ,若向该矩形内随机投一点 ,那么使 与 的面积都小于4的概率为( )A、
5. 在矩形 中, , ,若向该矩形内随机投一点 ,那么使 与 的面积都小于4的概率为( )A、 B、
B、 C、
C、 D、
6. 如图所示的程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的 分别为63,36,则输出的 ( )
D、
6. 如图所示的程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的 分别为63,36,则输出的 ( ) A、3 B、6 C、9 D、187. 已知数列 ,则 是数列 是递增数列的( )条件A、充分不必要 B、必要不充分 C、充要 D、既不充分也不必要8. 将函数 向右平移 个单位后得到函数 ,则 具有性质( )A、在
A、3 B、6 C、9 D、187. 已知数列 ,则 是数列 是递增数列的( )条件A、充分不必要 B、必要不充分 C、充要 D、既不充分也不必要8. 将函数 向右平移 个单位后得到函数 ,则 具有性质( )A、在 上单调递增,为偶函数
B、最大值为1,图象关于直线
上单调递增,为偶函数
B、最大值为1,图象关于直线  对称
C、在
对称
C、在  上单调递增,为奇函数
D、周期为
上单调递增,为奇函数
D、周期为 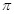 ,图象关于点
,图象关于点  对称
9. 在四边形 中, , ,则 ( )A、5 B、
对称
9. 在四边形 中, , ,则 ( )A、5 B、 C、
D、3
10. 已知函数 ( 为实数)为偶函数,且在 单调递减,则 的解集为( )A、 B、
C、
D、3
10. 已知函数 ( 为实数)为偶函数,且在 单调递减,则 的解集为( )A、 B、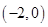 C、
C、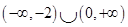 D、
D、 11. 若长方体 的顶点都在体积为 的球 的球面上,则长方体 的表面积的最大值等于( )A、576 B、288 C、144 D、7212. 对于实数 ,下列说法:①若 ,则 ;②若 ,则 ;③若 ,则 ;④若 ,且 ,则 ,其中正确的命题的个数( )A、1 B、2 C、3 D、4
11. 若长方体 的顶点都在体积为 的球 的球面上,则长方体 的表面积的最大值等于( )A、576 B、288 C、144 D、7212. 对于实数 ,下列说法:①若 ,则 ;②若 ,则 ;③若 ,则 ;④若 ,且 ,则 ,其中正确的命题的个数( )A、1 B、2 C、3 D、4二、填空题
-
13. .14. 通常,满分为 分的试卷, 分为及格线.若某次满分为 分的测试卷, 人参加测试,将这 人的卷面分数按照 , ,…, 分组后绘制的频率分布直方图如图所示.由于及格人数较少,某位老师准备将每位学生的卷面得分采用“开方乘以 取整”的方法进行换算以提高及格率(实数 的取整等于不超过 的最大整数),如:某位学生卷面 分,则换算成 分作为他的最终考试成绩,则按照这种方式,这次测试的及格率将变为 . (结果用小数表示)
 15. 函数 存在唯一的零点 ,且 ,则实数 的取值范围是 .
15. 函数 存在唯一的零点 ,且 ,则实数 的取值范围是 .三、解答题
-
16. 已知向量(1)、当 时,求 的值;(2)、已知钝角 中,角 为钝角, 分别为角 的对边,且 ,若函数 ,求 的值.17. 某调查机构对某校学生做了一个是否同意生“二孩”抽样调查,该调查机构从该校随机抽查了100名不同性别的学生,调查统计他们是同意父母生“二孩”还是反对父母生“二孩”,现已得知100人中同意父母生“二孩”占60%,统计情况如下表:
同意
不同意
合计
男生
a
5
女生
40
d
合计
100
附:
0.15
0.100
0.050
0.025
0.010
2.072
2.706
3.841
5.024
6.635
(1)、求 a , d 的值;(2)、根据以上数据,能否有97.5%的把握认为是否同意父母生“二孩”与性别有关?请说明理由;18. 若数列 的前 项和为 ,首项 ,且(1)、求数列 的通项公式;(2)、若 ,令 ,求数列 的前 项和 .19. 如图,四棱锥 中,侧面 为等边三角形,且平面 底面 , , . (1)、证明: ;(2)、点 在棱 上,且 ,若三棱锥 的体积为 ,求实数 的值.
(1)、证明: ;(2)、点 在棱 上,且 ,若三棱锥 的体积为 ,求实数 的值.