2016-2017学年安徽省滁州市九年级上学期期中数学试卷
试卷更新日期:2017-04-12 类型:期中考试
一、选择题:
-
1. 二次函数y=3x2﹣4的图象是一条抛物线,下列关于该抛物线的说法正确的是( )A、抛物线开口向下 B、抛物线经过点(3,4) C、抛物线的对称轴是直线x=1 D、抛物线与x轴有两个交点2. 一枚炮弹射出x秒后的高度为y米,且y与x之间的关系为y=ax2+bx+c(a≠0),若此炮弹在第3.2秒与第5.8秒时的高度相等,则在下列时间中炮弹所在高度最高的是( )A、第3.3s B、第4.3s C、第5.2s D、第4.6s3. 某村耕地总面积为50公顷,且该村人均耕地面积y(单位:公顷/人)与总人口x(单位:人)的函数图象如图所示,则下列说法正确的是( )
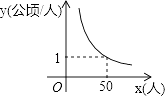 A、该村人均耕地面积随总人口的增多而增多 B、当该村总人口为50人时,人均耕地面积为1公顷 C、若该村人均耕地面积为2公顷,则总人口有100人 D、该村人均耕地面积y与总人口x成正比例4. 如图,在平面直角坐标中,菱形OABC的面积为12,点B在y轴上,点C在反比例函数y= 的图象上,则k的值为( )
A、该村人均耕地面积随总人口的增多而增多 B、当该村总人口为50人时,人均耕地面积为1公顷 C、若该村人均耕地面积为2公顷,则总人口有100人 D、该村人均耕地面积y与总人口x成正比例4. 如图,在平面直角坐标中,菱形OABC的面积为12,点B在y轴上,点C在反比例函数y= 的图象上,则k的值为( ) A、3 B、﹣3 C、6 D、﹣65. 如果x:y=2:3,则下列各式不成立的是( )A、 B、 C、 D、6. 如图,△ABC中,AD是中线,BC=8,∠B=∠DAC,则线段AC的长是( )
A、3 B、﹣3 C、6 D、﹣65. 如果x:y=2:3,则下列各式不成立的是( )A、 B、 C、 D、6. 如图,△ABC中,AD是中线,BC=8,∠B=∠DAC,则线段AC的长是( ) A、3 B、4 C、4 D、27. 下列命题错误的是( )A、相似三角形周长之比等于对应高之比 B、两个等腰直角三角形一定相似 C、各有一个角等于91°的两个等腰三角形相似 D、两边对应成比例且有一个角相等的两个三角形相似8. 如图,D、E分别是△ABC的边AB、BC上的点,且DE∥AC,AE、CD相交于点O,若S△DOE:S△COA=1:25,则S△BDE与S△CDE的比是( )
A、3 B、4 C、4 D、27. 下列命题错误的是( )A、相似三角形周长之比等于对应高之比 B、两个等腰直角三角形一定相似 C、各有一个角等于91°的两个等腰三角形相似 D、两边对应成比例且有一个角相等的两个三角形相似8. 如图,D、E分别是△ABC的边AB、BC上的点,且DE∥AC,AE、CD相交于点O,若S△DOE:S△COA=1:25,则S△BDE与S△CDE的比是( )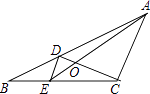 A、1:3 B、1:4 C、1:5 D、1:259. 二次函数y=ax2+bx+c(a≠0)的图象如图,则反比例函数 与一次函数y=bx﹣c在同一坐标系内的图象大致是( )
A、1:3 B、1:4 C、1:5 D、1:259. 二次函数y=ax2+bx+c(a≠0)的图象如图,则反比例函数 与一次函数y=bx﹣c在同一坐标系内的图象大致是( ) A、
A、 B、
B、 C、
C、 D、
D、 10. 如图,正△ABC的边长为4,点P为BC边上的任意一点(不与点B、C重合),且∠APD=60°,PD交AB于点D.设BP=x,BD=y,则y关于x的函数图象大致是( )
10. 如图,正△ABC的边长为4,点P为BC边上的任意一点(不与点B、C重合),且∠APD=60°,PD交AB于点D.设BP=x,BD=y,则y关于x的函数图象大致是( )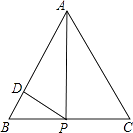 A、
A、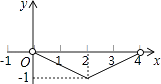 B、
B、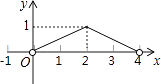 C、
C、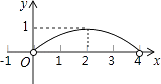 D、
D、
二、填空题:
-
11. 一司机驾驶汽车从甲地去乙地,他以80千米/小时的平均速度用了4小时到达乙地,当他按照原路返回时,汽车的速度v千米/小时与时间t小时的函数关系式是 .12. 如图,AB∥CD∥EF,AF与BE相交于点G,且AG=2,GD=1,DF=5,那么 的值等于 .
 13. 如图,在平面直角坐标系中,矩形AOCB的两边OA、OC分别在x轴和y轴上,且OA=2,OC=1.在第二象限内,将矩形AOCB以原点O为位似中心放大为原来的 倍,得到矩形A1OC1B1 , 再将矩形A1OC1B1以原点O为位似中心放大 倍,得到矩形A2OC2B2…,以此类推,得到的矩形AnOCnBn的对角线交点的坐标为 .
13. 如图,在平面直角坐标系中,矩形AOCB的两边OA、OC分别在x轴和y轴上,且OA=2,OC=1.在第二象限内,将矩形AOCB以原点O为位似中心放大为原来的 倍,得到矩形A1OC1B1 , 再将矩形A1OC1B1以原点O为位似中心放大 倍,得到矩形A2OC2B2…,以此类推,得到的矩形AnOCnBn的对角线交点的坐标为 . 14. 如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点B(4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:
14. 如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点B(4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:①2a+b=0;②abc>0;③方程ax2+bx+c=3有两个相等的实数根;④抛物线与x轴的另一个交点是(﹣1,0);⑤当1<x<4时,有y2<y1 ,
其中正确的是 .

三、解答题。
-
15. 如果二次函数y=x2﹣x+c的图象过点(1,2),求这个二次函数的解析式,并求出该函数图象的顶点坐标.16. 如图,在△PAB中,∠APB=120°,M,N是AB上两点,且△PMN是等边三角形,求证:BM•PA=PN•BP.
 17. 如图,矩形EFGH内接于△ABC,且边FG落在BC上,AD⊥BC,BC=3cm,AD=2cm,EF= EH,求EH的长.
17. 如图,矩形EFGH内接于△ABC,且边FG落在BC上,AD⊥BC,BC=3cm,AD=2cm,EF= EH,求EH的长. 18. 下表给出了代数式x2+bx+c与x的一些对应值:
18. 下表给出了代数式x2+bx+c与x的一些对应值:x
…
0
1
2
3
4
…
x2+bx+c
…
3
﹣1
3
…
(1)、请在表内的空格中填入适当的数;(2)、设y=x2+bx+c,则当x取何值时,y>0;(3)、请说明经过怎样平移函数y=x2+bx+c的图象得到函数y=x2的图象?19. 如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为D、E,AD与BE相交于点F.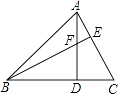 (1)、求证:△ACD∽△BFD;(2)、若∠ABD=45°,AC=3时,求BF的长.20. 在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm,花园的面积为S.
(1)、求证:△ACD∽△BFD;(2)、若∠ABD=45°,AC=3时,求BF的长.20. 在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm,花园的面积为S. (1)、求S与x之间的函数表达式;(2)、若在P处有一棵树与墙CD,AD的距离分别是15m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积的最大值.21. 如图,已知反比例函数y1= 的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,﹣2).
(1)、求S与x之间的函数表达式;(2)、若在P处有一棵树与墙CD,AD的距离分别是15m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积的最大值.21. 如图,已知反比例函数y1= 的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,﹣2). (1)、求这两个函数的表达式;(2)、观察图象,直接写出y1>y2时自变量x的取值范围.(3)、连接OA、OB,求△AOB的面积.22. 如图,矩形ABCD中AB=12cm,BC=6cm,点P沿AB边从点A开始以2cm/秒的速度移动,点Q沿DA边从D以1cm/秒的速度移动,若P、Q同时出发,用t表示移动时间(0≤t≤6),求当t何值时,△APQ与△ABC相似?
(1)、求这两个函数的表达式;(2)、观察图象,直接写出y1>y2时自变量x的取值范围.(3)、连接OA、OB,求△AOB的面积.22. 如图,矩形ABCD中AB=12cm,BC=6cm,点P沿AB边从点A开始以2cm/秒的速度移动,点Q沿DA边从D以1cm/秒的速度移动,若P、Q同时出发,用t表示移动时间(0≤t≤6),求当t何值时,△APQ与△ABC相似? 23. 如图,抛物线y=x2+bx+c与x轴交于A、B两点,B点坐标为(3,0),与y轴交于点C(0,﹣3)
23. 如图,抛物线y=x2+bx+c与x轴交于A、B两点,B点坐标为(3,0),与y轴交于点C(0,﹣3)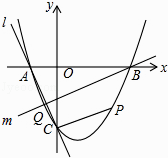 (1)、求抛物线的解析式;(2)、点P在抛物线位于第四象限的部分上运动,当四边形ABPC的面积最大时,求点P的坐标和四边形ABPC的最大面积.(3)、直线l经过A、C两点,点Q在抛物线位于y轴左侧的部分上运动,直线m经过点B和点Q,是否存在直线m,使得直线l、m与x轴围成的三角形和直线l、m与y轴围成的三角形相似?若存在,求出直线m的解析式,若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、点P在抛物线位于第四象限的部分上运动,当四边形ABPC的面积最大时,求点P的坐标和四边形ABPC的最大面积.(3)、直线l经过A、C两点,点Q在抛物线位于y轴左侧的部分上运动,直线m经过点B和点Q,是否存在直线m,使得直线l、m与x轴围成的三角形和直线l、m与y轴围成的三角形相似?若存在,求出直线m的解析式,若不存在,请说明理由.