四川省南充市2018-2019学年高三上学期文数第一次高考适应性考试试卷
试卷更新日期:2019-01-16 类型:高考模拟
一、单选题
-
1. 已知集合 , ,则 ( )A、
 B、
B、 C、
C、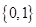 D、
D、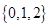 2. ( )A、
2. ( )A、 B、
B、 C、2
D、-2
3. 下列命题中的假命题是( )A、
C、2
D、-2
3. 下列命题中的假命题是( )A、 B、
B、 C、
C、 D、
D、 4. 是第四象限角, ,则 ( )A、 B、
4. 是第四象限角, ,则 ( )A、 B、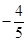 C、
C、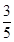 D、
D、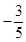 5. 在区间 内任取一实数 ,则 的概率是( )A、 B、 C、 D、6. 已知函数 的最小正周期为 ,则下列选项正确的是( )A、函数 的图像关于点
5. 在区间 内任取一实数 ,则 的概率是( )A、 B、 C、 D、6. 已知函数 的最小正周期为 ,则下列选项正确的是( )A、函数 的图像关于点 对称
B、函数 的图像关于点
对称
B、函数 的图像关于点  对称
C、函数 的图像关于直线
对称
C、函数 的图像关于直线  对称
D、函数 的图像关于直线
对称
D、函数 的图像关于直线  对称
7. 点 , 是圆 上的不同两点,且点 , 关于直线 对称,则该圆的半径等于( )A、
对称
7. 点 , 是圆 上的不同两点,且点 , 关于直线 对称,则该圆的半径等于( )A、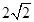 B、
B、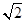 C、1
D、3
8. 已知函数 ,则函数 的图像大致是( )A、
C、1
D、3
8. 已知函数 ,则函数 的图像大致是( )A、 B、
B、 C、
C、 D、
D、 9. 将边长为2的正 沿高 折成直二面角 ,则三棱锥 的外接球的表面积是( )A、
9. 将边长为2的正 沿高 折成直二面角 ,则三棱锥 的外接球的表面积是( )A、 B、
B、 C、
C、 D、
D、 10. 的内角 , , 的对边分别为 , , ,若 , , 成等差数列, , 的面积为 ,则 ( )A、
10. 的内角 , , 的对边分别为 , , ,若 , , 成等差数列, , 的面积为 ,则 ( )A、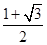 B、
B、 C、
C、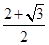 D、
D、
二、填空题
-
11. 已知函数 ( 且 )恒过定点 ,则 .12. 某校高三年级共有30个班,学校心理咨询室为了解同学们的心理状况,将每个班编号,依次为1到30,现用系统抽样的方法抽取6个班进行调查,若抽到的编号之和为87,则抽到的最小编号为 .13. 若变量 , 满足约束条件 则 的最大值是 .14. 已知函数 ,实数 满足 ,且 ,若 在 的最大值为2,则 .
三、解答题
-
15. 在数列 中, , .(1)、求 的通项公式;(2)、数列 是等差数列, 为 前 项和,若 , ,求 .16. 为了解某班学生喜好体育运动是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
喜好体育运动
不喜好体育运动
合计
男生
5
女生
10
合计
50
已知按喜好体育运动与否,采用分层抽样法抽取容量为10的样本,则抽到喜好体育运动的人数为6.
附:
0.10
0.05
0.025
0.010
2.706
3.841
5.024
6.635
(1)、请将上面的列联表补充完整;(2)、能否在犯错概率不超过0.01的前提下认为喜好体育运动与性别有关?说明理由.17. 如图,三棱柱 中, 平面 , 为正三角形, 是 边的中点, . (1)、求证:平面 平面 ;(2)、求点 到平面 的距离.18. 在直角坐标系 中,设椭圆 的左右两个焦点分别为 , ,过右焦点 且与 轴垂直的直线 与椭圆 相交,其中一个交点为 .(1)、求椭圆 的方程;(2)、若椭圆 的一个顶点为 ,直线 交椭圆 于另一点 ,求 的面积.
(1)、求证:平面 平面 ;(2)、求点 到平面 的距离.18. 在直角坐标系 中,设椭圆 的左右两个焦点分别为 , ,过右焦点 且与 轴垂直的直线 与椭圆 相交,其中一个交点为 .(1)、求椭圆 的方程;(2)、若椭圆 的一个顶点为 ,直线 交椭圆 于另一点 ,求 的面积.