2016-2017学年安徽省黄山市四校联考九年级上学期期中数学试卷
试卷更新日期:2017-04-12 类型:期中考试
一、选择题.
-
1. 下列方程中,关于x的一元二次方程是( )A、3(x+1)2=2(x+1) B、 C、ax2+bx+c=0 D、x2﹣x(x+7)=02. 以下是回收、绿色包装、节水、低碳四个标志,其中是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 将抛物线y=x2向左平移2个单位长度,再向下平移3个单位长度,得到的抛物线的函数表达式为( )A、y=(x+2)2﹣3 B、y=(x+2)2+3 C、y=(x﹣2)2+3 D、y=(x﹣2)2﹣34. 如图是二次函数y=ax2+bx+c的部分图象,由图象可知不等式ax2+bx+c<0的解集是( )
3. 将抛物线y=x2向左平移2个单位长度,再向下平移3个单位长度,得到的抛物线的函数表达式为( )A、y=(x+2)2﹣3 B、y=(x+2)2+3 C、y=(x﹣2)2+3 D、y=(x﹣2)2﹣34. 如图是二次函数y=ax2+bx+c的部分图象,由图象可知不等式ax2+bx+c<0的解集是( )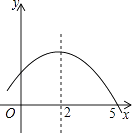 A、﹣1<x<5 B、x>5 C、x<﹣1且x>5 D、x<﹣1或x>55. 一元二次方程x(x﹣2)=2﹣x的根是( )A、﹣1 B、2 C、1和2 D、﹣1和26. 目前我国已建立了比较完善的经济困难学生资助体系,某校去年上半年发放给每个经济困难学生389元,今年上半年发放了438元,设每半年发放的资助金额的平均增长率为x,则下面列出的方程中正确的是( )A、438(1+x)2=389 B、389(1+x)2=438 C、389(1+2x)=438 D、438(1+2x)=3897.
A、﹣1<x<5 B、x>5 C、x<﹣1且x>5 D、x<﹣1或x>55. 一元二次方程x(x﹣2)=2﹣x的根是( )A、﹣1 B、2 C、1和2 D、﹣1和26. 目前我国已建立了比较完善的经济困难学生资助体系,某校去年上半年发放给每个经济困难学生389元,今年上半年发放了438元,设每半年发放的资助金额的平均增长率为x,则下面列出的方程中正确的是( )A、438(1+x)2=389 B、389(1+x)2=438 C、389(1+2x)=438 D、438(1+2x)=3897.如图,在宽度为20m,长为32m的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪,要使草坪的面积为540m2 , 求道路的宽.如果设小路宽为xm,根据题意,所列方程正确的是( )
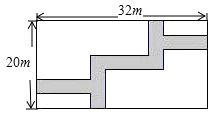 A、(20+x)(32﹣x)=540 B、(20﹣x)(32+x)=540 C、(20﹣x)(32﹣x)=540 D、(20+x)(32+x)=5408. 已知二次函数y=x2+(m﹣1)x+1,当x>1时,y随x的增大而增大,而m的取值范围是( )A、m=﹣1 B、m=3 C、m≤﹣1 D、m≥﹣19. 在平面直角坐标系中,A点坐标为(3,4),将线段OA绕原点O逆时针旋转90°得到线段OA′,则点A′的坐标是( )A、(﹣4,3) B、(﹣3,4) C、(3,﹣4) D、(4,﹣3)10. 如图,边长为1的正方形ABCD绕点A逆时针旋转30°到正方形AB′C′D′,图中阴影部分的面积为( )
A、(20+x)(32﹣x)=540 B、(20﹣x)(32+x)=540 C、(20﹣x)(32﹣x)=540 D、(20+x)(32+x)=5408. 已知二次函数y=x2+(m﹣1)x+1,当x>1时,y随x的增大而增大,而m的取值范围是( )A、m=﹣1 B、m=3 C、m≤﹣1 D、m≥﹣19. 在平面直角坐标系中,A点坐标为(3,4),将线段OA绕原点O逆时针旋转90°得到线段OA′,则点A′的坐标是( )A、(﹣4,3) B、(﹣3,4) C、(3,﹣4) D、(4,﹣3)10. 如图,边长为1的正方形ABCD绕点A逆时针旋转30°到正方形AB′C′D′,图中阴影部分的面积为( )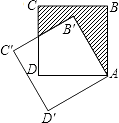 A、 B、 C、1﹣ D、1﹣
A、 B、 C、1﹣ D、1﹣二、填空题:
-
11. 正五角星绕它的中心旋转一定的角度后能与自身完全重合,则其旋转的角度至少为 .12. 新世纪百货大楼“宝乐”牌童装平均每天可售出20件,每件盈利40元.为了迎接“六一”儿童节,商场决定采取适当的降价措施.经调査,如果每件童装降价1元,那么平均每天就可多售出2件.要想平均每天销售这种童装盈利1200元,则每件童装应降价多少元?设每件童装应降价x元,可列方程为 .13. 若抛物线y=(x﹣m)2+(m+1)的顶点在第一象限,则m的取值范围为。
14. 如图为二次函数y=ax2+bx+c的图象,在下列说法中:①ac<0;
②方程ax2+bx+c=0的根是x1=﹣1,x2=3;
③a+b+c>0;
④当x>1时,y随着x的增大而增大.
正确的说法有 . (请写出所有正确的序号)

三、解答题
-
15. 解方程:(x﹣2)(x﹣5)=﹣2.16. 已知关于x的一元二次方程(a+c)x2+2bx+(a﹣c)=0,其中a、b、c分别为△ABC三边的长.(1)、如果x=﹣1是方程的根,试判断△ABC的形状,并说明理由;(2)、如果方程有两个相等的实数根,试判断△ABC的形状,并说明理由.17. 如果x2﹣10x+y2﹣16y+89=0,求 的值.18.
如图,每个小方格都是边长为1个单位长度的小正方形.
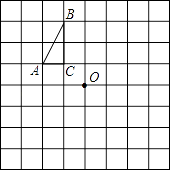 (1)、将△ABC向右平移3个单位长度,画出平移后的△A1B1C1 .(2)、将△ABC绕点O旋转180°,画出旋转后的△A2B2C2 .(3)、画出一条直线将△AC1A2的面积分成相等的两部分.19. 在某市组织的大型商业演出活动中,对团体购买门票实行优惠,决定在原定票价基础上每张降价80元,这样按原定票价需花费6000元购买的门票张数,现在只花费了4800元.(1)、求每张门票的原定票价;(2)、根据实际情况,活动组织单位决定对于个人购票也采取优惠政策,原定票价经过连续二次降价后降为324元,求平均每次降价的百分率.20. 某工厂生产的某种产品按质量分为10个档次,第1档次(最低档次)的产品一天能生产95件,每件利润6元.每提高一个档次,每件利润增加2元,但一天产量减少5件.(1)、若生产第x档次的产品一天的总利润为y元(其中x为正整数,且1≤x≤10),求出y关于x的函数关系式;(2)、若生产第x档次的产品一天的总利润为1120元,求该产品的质量档次.21. 如图1,正方形ABCD与正方形AEFG的边AB、AE(AB<AE)在一条直线上,正方形AEFG以点A为旋转中心逆时针旋转,设旋转角为α.在旋转过程中,两个正方形只有点A重合,其它顶点均不重合,连接BE、DG.
(1)、将△ABC向右平移3个单位长度,画出平移后的△A1B1C1 .(2)、将△ABC绕点O旋转180°,画出旋转后的△A2B2C2 .(3)、画出一条直线将△AC1A2的面积分成相等的两部分.19. 在某市组织的大型商业演出活动中,对团体购买门票实行优惠,决定在原定票价基础上每张降价80元,这样按原定票价需花费6000元购买的门票张数,现在只花费了4800元.(1)、求每张门票的原定票价;(2)、根据实际情况,活动组织单位决定对于个人购票也采取优惠政策,原定票价经过连续二次降价后降为324元,求平均每次降价的百分率.20. 某工厂生产的某种产品按质量分为10个档次,第1档次(最低档次)的产品一天能生产95件,每件利润6元.每提高一个档次,每件利润增加2元,但一天产量减少5件.(1)、若生产第x档次的产品一天的总利润为y元(其中x为正整数,且1≤x≤10),求出y关于x的函数关系式;(2)、若生产第x档次的产品一天的总利润为1120元,求该产品的质量档次.21. 如图1,正方形ABCD与正方形AEFG的边AB、AE(AB<AE)在一条直线上,正方形AEFG以点A为旋转中心逆时针旋转,设旋转角为α.在旋转过程中,两个正方形只有点A重合,其它顶点均不重合,连接BE、DG.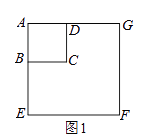 (1)、当正方形AEFG旋转至如图2所示的位置时,求证:BE=DG;
(1)、当正方形AEFG旋转至如图2所示的位置时,求证:BE=DG;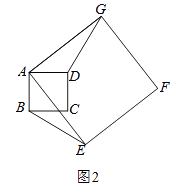 (2)、如图3,如果α=45°,AB=2,AE=4 ,求点G到BE的距离.
(2)、如图3,如果α=45°,AB=2,AE=4 ,求点G到BE的距离.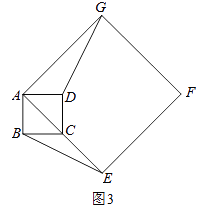 22. 已知二次函数y=x2﹣2mx+m2+3(m是常数).(1)、求证:不论m为何值,该函数的图象与x轴没有公共点;(2)、把该函数的图象沿y轴向下平移多少个单位长度后,得到的函数的图象与x轴只有一个公共点?23.
22. 已知二次函数y=x2﹣2mx+m2+3(m是常数).(1)、求证:不论m为何值,该函数的图象与x轴没有公共点;(2)、把该函数的图象沿y轴向下平移多少个单位长度后,得到的函数的图象与x轴只有一个公共点?23.如图,在平面直角坐标系中,直线y=﹣ x﹣ 与x轴交于点A,与y轴交于点C,抛物线y=ax2﹣ x+c(a≠0)经过A,B,C三点.
 (1)、求过A,B,C三点抛物线的解析式并求出顶点F的坐标;(2)、在抛物线上是否存在点P,使△ABP为直角三角形?若存在,直接写出P点坐标;若不存在,请说明理由;(3)、试探究在直线AC上是否存在一点M,使得△MBF的周长最小?若存在,求出M点的坐标;若不存在,请说明理由.
(1)、求过A,B,C三点抛物线的解析式并求出顶点F的坐标;(2)、在抛物线上是否存在点P,使△ABP为直角三角形?若存在,直接写出P点坐标;若不存在,请说明理由;(3)、试探究在直线AC上是否存在一点M,使得△MBF的周长最小?若存在,求出M点的坐标;若不存在,请说明理由.