四川省泸州市2018-2019学年高三上学期文数第一次教学质量诊断性考试试卷
试卷更新日期:2019-01-16 类型:高考模拟
一、单选题
-
1. 已知集合 , ,则 ( )A、
 B、
B、 C、
C、 D、
D、 2. 命题“ , ”的否定是( )A、不存在
2. 命题“ , ”的否定是( )A、不存在 ,使
,使  B、
B、 ,使
,使  C、
C、 ,使
,使  D、
D、 ,使
,使  3. 设 , , ,则下列关系正确的是( )A、
3. 设 , , ,则下列关系正确的是( )A、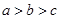 B、
B、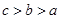 C、
C、 D、
D、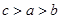 4. 已知函数 ,则函数 的最小正周期为( )A、 B、 C、 D、5. 函数 的图像大致为( )A、
4. 已知函数 ,则函数 的最小正周期为( )A、 B、 C、 D、5. 函数 的图像大致为( )A、 B、
B、 C、
C、 D、
D、 6. 若 是两条不同的直线, 垂直于平面 ,则“ ”是“ ”的( )A、充分而不必要条件 B、必要而不充分条件 C、充分必要条件 D、既不充分也不必要条件7. 实数 , 满足 ,则下列关系正确的是( )A、
6. 若 是两条不同的直线, 垂直于平面 ,则“ ”是“ ”的( )A、充分而不必要条件 B、必要而不充分条件 C、充分必要条件 D、既不充分也不必要条件7. 实数 , 满足 ,则下列关系正确的是( )A、 B、
B、 C、
C、 D、
D、 8. 在 中, , , ,将 绕 所在的直线旋转一周而形成的曲面所围成的几何体的表面积为( )A、
8. 在 中, , , ,将 绕 所在的直线旋转一周而形成的曲面所围成的几何体的表面积为( )A、 B、
B、 C、
C、 D、
D、 9. 如图,网格纸是边长为1的小正方形,在其上用粗线画出了某多面体的三视图,则该多面体的体积为( )
9. 如图,网格纸是边长为1的小正方形,在其上用粗线画出了某多面体的三视图,则该多面体的体积为( ) A、16 B、8 C、4 D、2010. 《周髀算经》中给出了弦图,所谓弦图是由四个全等的直角三角形和中间一个小正方形拼成一个大的正方形,若图中直角三角形的一个锐角为 ,且小正方形与大正方形面积之比为 ,则 的值为( )
A、16 B、8 C、4 D、2010. 《周髀算经》中给出了弦图,所谓弦图是由四个全等的直角三角形和中间一个小正方形拼成一个大的正方形,若图中直角三角形的一个锐角为 ,且小正方形与大正方形面积之比为 ,则 的值为( ) A、 B、 C、
A、 B、 C、 D、
D、 11. 已知函数 的部分图象如图所示,将函数 的图象上所有点的横坐标缩短为原来的 ,纵坐标不变,再将所得图象上所有点向右平移 个单位长度,得到的函数图象关于直线 对称,则 的最小值为( )
11. 已知函数 的部分图象如图所示,将函数 的图象上所有点的横坐标缩短为原来的 ,纵坐标不变,再将所得图象上所有点向右平移 个单位长度,得到的函数图象关于直线 对称,则 的最小值为( ) A、
A、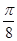 B、
C、
D、
12. 已知函数 的值域与函数 的值域相同,则 的取值范围为( )A、
B、
C、
D、
12. 已知函数 的值域与函数 的值域相同,则 的取值范围为( )A、 B、
B、 C、
C、 D、
D、
二、填空题
-
13. 已知函数 ,若 ,则 .14. 在 中,角 , , 所对的边分别为 , , ,若 ,则角 的大小为.15. 已知函数 ,则 的解集为.16. 已知三棱锥 的所有顶点都在同一球面上,底面 是正三角形且和球心 在同一平面内,若此三棱锥的最大体积为 ,则球 的表面积等于 .
三、解答题
-
17. 在 中,角 , , 所对的边分别是 , , ,已知 , .(1)、若 ,求 的值;(2)、 的面积为 ,求 的值.18. 已知函数 .(1)、当 时,求曲线 在 处的切线方程;(2)、若函数 在区间 上是增函数,求实数 的取值范围.19. 如图,在平面直角坐标系 中,点 、 都在单位圆 上, ,且 .
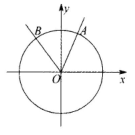 (1)、若 ,求 的值;(2)、若 ,求 的取值范围.20. 如图,在四棱锥 中,底面 是平行四边形,且 , ,平面 平面 .
(1)、若 ,求 的值;(2)、若 ,求 的取值范围.20. 如图,在四棱锥 中,底面 是平行四边形,且 , ,平面 平面 . (1)、求证: ;(2)、若底面 是边长为2的菱形,四棱锥 的体积为 ,求点 到平面 的距离.
(1)、求证: ;(2)、若底面 是边长为2的菱形,四棱锥 的体积为 ,求点 到平面 的距离.