四川省凉山州2018-2019学年高中毕业班文数第一次诊断性检测试卷
试卷更新日期:2019-01-16 类型:高考模拟
一、单选题
-
1. 设集合 ,集合 ,则 ( )A、
 B、
B、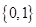 C、
C、 D、
D、 2. 下列函数中,既是奇函数,又在区间 递减的函数是( )A、
2. 下列函数中,既是奇函数,又在区间 递减的函数是( )A、 B、
B、 C、
C、 D、
D、 3. 已知双曲线 的渐近线方程是 ,则 的离心率为( )A、 或2 B、 C、
3. 已知双曲线 的渐近线方程是 ,则 的离心率为( )A、 或2 B、 C、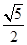 D、 或
D、 或 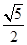 4. 如图,四棱柱 中, 分别是 、 的中点,下列结论中,正确的是( )
4. 如图,四棱柱 中, 分别是 、 的中点,下列结论中,正确的是( ) A、
A、 B、
B、 平面
平面  C、
C、 平面
平面  D、
D、 平面
平面  5. 设 是边长为2的正三角形, 是 的中点, 是 的中点,则 的值为( )A、3 B、 C、4 D、
5. 设 是边长为2的正三角形, 是 的中点, 是 的中点,则 的值为( )A、3 B、 C、4 D、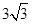 6. 执行如图所示的程序框图,输出 的值为( )
6. 执行如图所示的程序框图,输出 的值为( ) A、
A、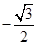 B、
C、
D、
7. 已知 ,则“ ”是“ ”成立的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要8. 函数 的最小正周期为( )A、 B、 C、 D、9. 数列 满足 , , 表示 的前 项和,且 ,则 ( )A、6 B、7 C、8 D、910. 在 中, 分别是内角 的对边,若 , , ,则 的面积等于( )A、
B、
C、
D、
7. 已知 ,则“ ”是“ ”成立的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要8. 函数 的最小正周期为( )A、 B、 C、 D、9. 数列 满足 , , 表示 的前 项和,且 ,则 ( )A、6 B、7 C、8 D、910. 在 中, 分别是内角 的对边,若 , , ,则 的面积等于( )A、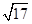 B、
C、
B、
C、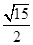 D、3
11. 十七世纪法国数学家费马提出猜想:“当整数 时,关于 的方程 没有正整数解”.经历三百多年,于二十世纪九十年中期由英国数学家安德鲁 怀尔斯证明了费马猜想,使它终成费马大定理,则下面说法正确的是( )A、存在至少一组正整数组
D、3
11. 十七世纪法国数学家费马提出猜想:“当整数 时,关于 的方程 没有正整数解”.经历三百多年,于二十世纪九十年中期由英国数学家安德鲁 怀尔斯证明了费马猜想,使它终成费马大定理,则下面说法正确的是( )A、存在至少一组正整数组 使方程
使方程  有解
B、关于
有解
B、关于  的方程
的方程  有正有理数解
C、关于
有正有理数解
C、关于  的方程
的方程  没有正有理数解
D、当整数
没有正有理数解
D、当整数  时,关于
时,关于  的方程
的方程  没有正实数解
12. 若 都有 成立,则 的最大值为( )A、 B、1 C、
没有正实数解
12. 若 都有 成立,则 的最大值为( )A、 B、1 C、 D、
D、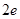
二、填空题
-
13. 是虚数单位,复数 .14. 函数 的值域是 .15. 设 是椭圆 的左右焦点, 是椭圆 上的点,则 的最小值是 .16. 定义函数 , ,其中 ,符号 表示数 中的较大者,给出以下命题:① 是奇函数;②若不等式 对一切实数 恒成立,则 ③ 时, 最小值是2450④“ ”是“ ”成立的充要条件,以上正确命题是 . (写出所有正确命题的序号)
三、解答题
-
17. 从某市统考的学生数学考试卷中随机抽查100份数学试卷作为样本,分别统计出这些试卷总分,由总分得到如下的频率分别直方图.
 (1)、求这100份数学试卷成绩的中位数;(2)、从总分在 和 的试卷中随机抽取2份试卷,求抽取的2份试卷中至少有一份总分少于65分的概率.18. 如图,直三棱柱 中, , , , ,点 是棱 上不同于 的动点.
(1)、求这100份数学试卷成绩的中位数;(2)、从总分在 和 的试卷中随机抽取2份试卷,求抽取的2份试卷中至少有一份总分少于65分的概率.18. 如图,直三棱柱 中, , , , ,点 是棱 上不同于 的动点. (1)、证明: ;(2)、若 是 的中点,求四面体 的体积.19. 设有三点 ,其中点 在椭圆 上, , ,且 .(1)、求椭圆 的方程;(2)、若过椭圆 的右焦点的直线 倾斜角为 ,直线 与椭圆 相交于 ,求三角形 的面积.20. 设数列 中, , ,且数列 是以2为公比的等比数列.(1)、求数列 的通项公式;(2)、求数列 的前 项和 .
(1)、证明: ;(2)、若 是 的中点,求四面体 的体积.19. 设有三点 ,其中点 在椭圆 上, , ,且 .(1)、求椭圆 的方程;(2)、若过椭圆 的右焦点的直线 倾斜角为 ,直线 与椭圆 相交于 ,求三角形 的面积.20. 设数列 中, , ,且数列 是以2为公比的等比数列.(1)、求数列 的通项公式;(2)、求数列 的前 项和 .