四川省成都市龙泉驿区2018-2019学年高三理数统一模拟考试试卷
试卷更新日期:2019-01-16 类型:高考模拟
一、单选题
-
1. 设集合 , ,则集合 为( )A、
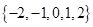 B、
B、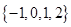 C、
C、 D、
D、 2. 在复平面内,复数z的对应点为(1,1),则z2=( )A、 B、2i C、 D、2+2i3. 已 知 , , 则 等 于( )A、
2. 在复平面内,复数z的对应点为(1,1),则z2=( )A、 B、2i C、 D、2+2i3. 已 知 , , 则 等 于( )A、 B、
B、 C、
C、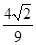 D、
D、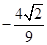 4. 若双曲线 的一条渐近线方程为 ,该双曲线的离心率是( )A、
4. 若双曲线 的一条渐近线方程为 ,该双曲线的离心率是( )A、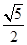 B、
C、
D、
5. 如图, 是以正方形的边 为直径的半圆,向正方形内随机投入一点,则该点落在阴影区域内的概率为( )
B、
C、
D、
5. 如图, 是以正方形的边 为直径的半圆,向正方形内随机投入一点,则该点落在阴影区域内的概率为( ) A、
A、 B、
C、
D、
6. 设m,n是两条不同的直线,α,β是两个不同的平面,则下列命题中正确的是( )A、若α⊥β,m⊥α,则m∥β B、若m∥α,n⊂α,则m∥n C、若α∩β=m,n∥α,n∥β,则m∥n D、若α⊥β,且α∩β=m,点A∈α,直线AB⊥m,则AB⊥β7. 某四棱锥的三视图如图所示,则该四棱锥的外接球半径为( )
B、
C、
D、
6. 设m,n是两条不同的直线,α,β是两个不同的平面,则下列命题中正确的是( )A、若α⊥β,m⊥α,则m∥β B、若m∥α,n⊂α,则m∥n C、若α∩β=m,n∥α,n∥β,则m∥n D、若α⊥β,且α∩β=m,点A∈α,直线AB⊥m,则AB⊥β7. 某四棱锥的三视图如图所示,则该四棱锥的外接球半径为( )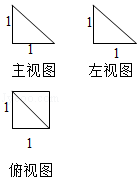 A、1 B、 C、
A、1 B、 C、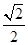 D、
8. 已知 为直线 上的点,过点 作圆 的切线,切点为 , ,若 ,则这样的点 有( )A、 个 B、 个 C、 个 D、无数个9. 函数 ,则不等式 的解集为( )A、
D、
8. 已知 为直线 上的点,过点 作圆 的切线,切点为 , ,若 ,则这样的点 有( )A、 个 B、 个 C、 个 D、无数个9. 函数 ,则不等式 的解集为( )A、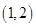 B、
B、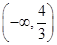 C、
C、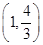 D、
D、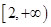 10. 函数 在区间 上的图象大致为( )A、
10. 函数 在区间 上的图象大致为( )A、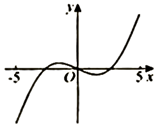 B、
B、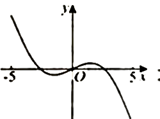 C、
C、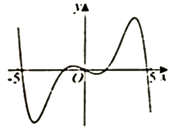 D、
D、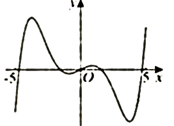 11. 已知抛物线 为 轴负半轴上的动点, 为抛物线的切线, 分别为切点,则 的最小值为 ( )A、 B、
11. 已知抛物线 为 轴负半轴上的动点, 为抛物线的切线, 分别为切点,则 的最小值为 ( )A、 B、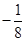 C、
C、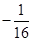 D、
12. 将函数 的图象向右平移 个单位后得到函数 的图象 若对满足 的 、 ,有 ,则A、
D、
12. 将函数 的图象向右平移 个单位后得到函数 的图象 若对满足 的 、 ,有 ,则A、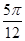 B、
C、
D、
B、
C、
D、
二、填空题
-
13. 已知 , 均为单位向量,且它们的夹角为120°,则|4 + |= .14. 二项式(x2﹣ )6的展开式中的常数项是 .15. 在△ABC中,a=2,b= ,B= ,则A= .16. 若函数f(x)=﹣ x﹣ cos2x+m(sinx﹣cosx)在(﹣∞,+∞)上单调递减,则m的取值范围是 .
三、解答题
-
17. 已知数列 的前项和(1)、求数列 的通项公式(2)、设数列 满足 ,求数列 的前n项和Tn18. 如图,在三棱台ABC﹣A1B1C1中,D,E分别是AB,AC的中点,B1E⊥平面ABC,△AB1C是等边三角形,AB=2A1B1 , AC=2BC,∠ACB=90°.

(Ⅰ)证明:B1C∥平面A1DE;
(Ⅱ)求二面角A﹣BB1﹣C的余弦值.
19. “微信运动”是一个类似计步数据库的公众账号.用户只需以运动手环或手机协处理器的运动数据为介,然后关注该公众号,就能看见自己与好友每日行走的步数,并在同一排行榜上得以体现.现随机选取朋友圈中的50人,记录了他们某一天的走路步数,并将数据整理如下:步数/步
10000以上
男生人数/人
1
2
7
15
5
女性人数/人
0
3
7
9
1
规定:人一天行走的步数超过8000步时被系统评定为“积极性”,否则为“懈怠性”.
(1)、以这50人这一天行走的步数的频率代替1人一天行走的步数发生的概率,记 表示随机抽取3人中被系统评为“积极性”的人数,求 和 的数学期望.(2)、为调查评定系统的合理性,拟从这50人中先抽取10人(男性6人,女性4人).其中男性中被系统评定为“积极性”的有4人,“懈怠性”的有2人,从中任意选取3人,记选到“积极性”的人数为 ;其中女性中被系统评定为“积极性”和“懈怠性”的各有2人,从中任意选取2人,记选到“积极性”的人数为 ;求 的概率.
20. 已知椭圆C: + =1(a>b>0)的离心率为 ,直线l:x+2y=4与椭圆有且只有一个交点T.(I)求椭圆C的方程和点T的坐标;
(Ⅱ)O为坐标原点,与OT平行的直线l′与椭圆C交于不同的两点A,B,直线l′与直线l交于点P,试判断 是否为定值,若是请求出定值,若不是请说明理由.