2018-2019学年初中数学北师大版九年级下册第二章《二次函数》检测题A
试卷更新日期:2019-01-15 类型:单元试卷
一、选择题
-
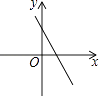
1. 用配方法将二次函数y=x2﹣8x﹣9化为y=a(x﹣h)2+k的形式为( )A、y=(x﹣4)2+7 B、y=(x﹣4)2﹣25 C、y=(x+4)2+7 D、y=(x+4)2﹣252. 下列对二次函数y=x2﹣x的图象的描述,正确的是( )A、开口向下 B、对称轴是y轴 C、经过原点 D、在对称轴右侧部分是下降的3. 已知一次函数y= x+c的图象如图,则二次函数y=ax2+bx+c在平面直角坐标系中的图象可能是( )
 A、
A、 B、
B、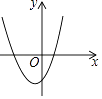 C、
C、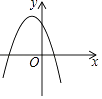 D、
D、 4. 若对于任意非零实数a,抛物线y=ax2+ax﹣2a总不经过点P(x0﹣3,x02﹣16),则符合条件的点P( )A、有且只有1个 B、有且只有2个 C、至少有3个 D、有无穷多个5. 将抛物线y=x2向左平移2个单位,再向下平移5个单位,平移后所得新抛物线的表达式为( )A、y=(x+2)2﹣5 B、y=(x+2)2+5 C、y=(x﹣2)2﹣5 D、y=(x﹣2)2+56. 如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc>0;②b﹣a>c;③4a+2b+c>0;④3a>﹣c;⑤a+b>m(am+b)(m≠1的实数).其中正确结论的有( )
4. 若对于任意非零实数a,抛物线y=ax2+ax﹣2a总不经过点P(x0﹣3,x02﹣16),则符合条件的点P( )A、有且只有1个 B、有且只有2个 C、至少有3个 D、有无穷多个5. 将抛物线y=x2向左平移2个单位,再向下平移5个单位,平移后所得新抛物线的表达式为( )A、y=(x+2)2﹣5 B、y=(x+2)2+5 C、y=(x﹣2)2﹣5 D、y=(x﹣2)2+56. 如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc>0;②b﹣a>c;③4a+2b+c>0;④3a>﹣c;⑤a+b>m(am+b)(m≠1的实数).其中正确结论的有( ) A、①②③ B、②③⑤ C、②③④ D、③④⑤7. 已知二次函数y=x2﹣2mx(m为常数),当﹣1≤x≤2时,函数值y的最小值为﹣2,则m的值是( )A、 B、 C、 或 D、- 或8. 如图,在Rt△ABC中,∠C=90°,AC=6cm,BC=2cm,点P在边AC上,从点A向点C移动,点Q在边CB上,从点C向点B移动.若点P,Q均以1cm/s的速度同时出发,且当一点移动到终点时,另一点也随之停止,连接PQ,则线段PQ的最小值是( )
A、①②③ B、②③⑤ C、②③④ D、③④⑤7. 已知二次函数y=x2﹣2mx(m为常数),当﹣1≤x≤2时,函数值y的最小值为﹣2,则m的值是( )A、 B、 C、 或 D、- 或8. 如图,在Rt△ABC中,∠C=90°,AC=6cm,BC=2cm,点P在边AC上,从点A向点C移动,点Q在边CB上,从点C向点B移动.若点P,Q均以1cm/s的速度同时出发,且当一点移动到终点时,另一点也随之停止,连接PQ,则线段PQ的最小值是( )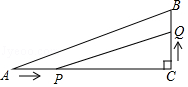 A、20cm B、18cm C、2 cm D、3 cm9. 如图,二次函数y=x2+bx+c的图象过点B(0,﹣2).它与反比例函数y=﹣ 的图象交于点A(m,4),则这个二次函数的解析式为( )
A、20cm B、18cm C、2 cm D、3 cm9. 如图,二次函数y=x2+bx+c的图象过点B(0,﹣2).它与反比例函数y=﹣ 的图象交于点A(m,4),则这个二次函数的解析式为( ) A、y=x2﹣x﹣2 B、y=x2﹣x+2 C、y=x2+x﹣2 D、y=x2+x+210. 一位篮球运动员在距离篮圈中心水平距离4m处起跳投篮,球沿一条抛物线运动,当球运动的水平距离为2.5m时,达到最大高度3.5m,然后准确落入篮框内.已知篮圈中心距离地面高度为3.05m,在如图所示的平面直角坐标系中,下列说法正确的是( )
A、y=x2﹣x﹣2 B、y=x2﹣x+2 C、y=x2+x﹣2 D、y=x2+x+210. 一位篮球运动员在距离篮圈中心水平距离4m处起跳投篮,球沿一条抛物线运动,当球运动的水平距离为2.5m时,达到最大高度3.5m,然后准确落入篮框内.已知篮圈中心距离地面高度为3.05m,在如图所示的平面直角坐标系中,下列说法正确的是( ) A、此抛物线的解析式是y=﹣ x2+3.5 B、篮圈中心的坐标是(4,3.05) C、此抛物线的顶点坐标是(3.5,0) D、篮球出手时离地面的高度是2m11. 抛物线C1:y1=mx2﹣4mx+2n﹣1与平行于x轴的直线交于A、B两点,且A点坐标为(﹣1,2),请结合图象分析以下结论:①对称轴为直线x=2;②抛物线与y轴交点坐标为(0,﹣1);③m> ;④若抛物线C2:y2=ax2(a≠0)与线段AB恰有一个公共点,则a的取值范围是 ≤a<2;⑤不等式mx2﹣4mx+2n>0的解作为函数C1的自变量的取值时,对应的函数值均为正数,其中正确结论的个数有( )
A、此抛物线的解析式是y=﹣ x2+3.5 B、篮圈中心的坐标是(4,3.05) C、此抛物线的顶点坐标是(3.5,0) D、篮球出手时离地面的高度是2m11. 抛物线C1:y1=mx2﹣4mx+2n﹣1与平行于x轴的直线交于A、B两点,且A点坐标为(﹣1,2),请结合图象分析以下结论:①对称轴为直线x=2;②抛物线与y轴交点坐标为(0,﹣1);③m> ;④若抛物线C2:y2=ax2(a≠0)与线段AB恰有一个公共点,则a的取值范围是 ≤a<2;⑤不等式mx2﹣4mx+2n>0的解作为函数C1的自变量的取值时,对应的函数值均为正数,其中正确结论的个数有( ) A、2个 B、3个 C、4个 D、5个12. 如图所示,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(﹣2,0)、B(1,0),直线x=﹣0.5与此抛物线交于点C,与x轴交于点M,在直线上取点D,使MD=MC,连接AC、BC、AD、BD,某同学根据图象写出下列结论:
A、2个 B、3个 C、4个 D、5个12. 如图所示,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(﹣2,0)、B(1,0),直线x=﹣0.5与此抛物线交于点C,与x轴交于点M,在直线上取点D,使MD=MC,连接AC、BC、AD、BD,某同学根据图象写出下列结论:①a﹣b=0;②当﹣2<x<1时,y>0;③四边形ACBD是菱形;④9a﹣3b+c>0
你认为其中正确的是( )
 A、②③④ B、①②④ C、①③④ D、①②③
A、②③④ B、①②④ C、①③④ D、①②③二、填空题
-
13. 已知函数 使 成立的 的值恰好只有 个时, 的值为.14. 如图,已知抛物线y1=﹣x2+4x和直线y2=2x.我们规定:当x取任意一个值时,x对应的函数值分别为y1和y2 , 若y1≠y2 , 取y1和y2中较小值为M;若y1=y2 , 记M=y1=y2 . ①当x>2时,M=y2;②当x<0时,M随x的增大而增大;③使得M大于4的x的值不存在;④若M=2,则x=1.上述结论正确的是(填写所有正确结论的序号).
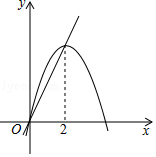 15. 如图,在边长为6cm的正方形ABCD中,点E、F、G、H分别从点A、B、C、D同时出发,均以1cm/s的速度向点B、C、D、A匀速运动,当点E到达点B时,四个点同时停止运动,在运动过程中,当运动时间为 s时,四边形EFGH的面积最小,其最小值是 cm2 .
15. 如图,在边长为6cm的正方形ABCD中,点E、F、G、H分别从点A、B、C、D同时出发,均以1cm/s的速度向点B、C、D、A匀速运动,当点E到达点B时,四个点同时停止运动,在运动过程中,当运动时间为 s时,四边形EFGH的面积最小,其最小值是 cm2 . 16. 如图,已知直线y=﹣ x+3分别交x轴、y轴于点A、B,P是抛物线y=﹣ x2+2x+5上的一个动点,其横坐标为a,过点P且平行于y轴的直线交直线y=﹣ x+3于点Q,则当PQ=BQ时,a的值是 .
16. 如图,已知直线y=﹣ x+3分别交x轴、y轴于点A、B,P是抛物线y=﹣ x2+2x+5上的一个动点,其横坐标为a,过点P且平行于y轴的直线交直线y=﹣ x+3于点Q,则当PQ=BQ时,a的值是 . 17. 如图,在平面直角坐标系中,抛物线y=x2+mx交x轴的负半轴于点A.点B是y轴正半轴上一点,点A关于点B的对称点A′恰好落在抛物线上.过点A′作x轴的平行线交抛物线于另一点C.若点A′的横坐标为1,则A′C的长为 .
17. 如图,在平面直角坐标系中,抛物线y=x2+mx交x轴的负半轴于点A.点B是y轴正半轴上一点,点A关于点B的对称点A′恰好落在抛物线上.过点A′作x轴的平行线交抛物线于另一点C.若点A′的横坐标为1,则A′C的长为 .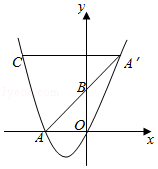 18. 如图抛物线y=x2+2x﹣3与x轴交于A,B两点,与y轴交于点C,点P是抛物线对称轴上任意一点,若点D、E、F分别是BC、BP、PC的中点,连接DE,DF,则DE+DF的最小值为 .
18. 如图抛物线y=x2+2x﹣3与x轴交于A,B两点,与y轴交于点C,点P是抛物线对称轴上任意一点,若点D、E、F分别是BC、BP、PC的中点,连接DE,DF,则DE+DF的最小值为 .
三、解答题
-
19. 如图,抛物线y=﹣x2+bx+c经过A(﹣1,0),B(3,0)两点,交y轴于点C,点D为抛物线的顶点,连接BD,点H为BD的中点.请解答下列问题:
 (1)、求抛物线的解析式及顶点D的坐标;(2)、在y轴上找一点P,使PD+PH的值最小,则PD+PH的最小值为 .
(1)、求抛物线的解析式及顶点D的坐标;(2)、在y轴上找一点P,使PD+PH的值最小,则PD+PH的最小值为 .(注:抛物线y=ax2+bx+c(a≠0)的对称轴是直线x=﹣ ,顶点坐标为(﹣ , )
20. 某商家销售一款商品,进价每件80元,售价每件145元,每天销售40件,每销售一件需支付给商场管理费5元,未来一个月 按30天计算 ,这款商品将开展“每天降价1元”的促销活动,即从第一天开始每天的单价均比前一天降低1元,通过市场调查发现,该商品单价每降1元,每天销售量增加2件,设第x天 且x为整数 的销售量为y件.
(1)、直接写出y与x的函数关系式;
(2)、设第x天的利润为w元,试求出w与x之间的函数关系式,并求出哪一天的利润最大?最大利润是多少元?
21. 已知抛物线L:y=x2+x﹣6与x轴相交于A、B两点(点A在点B的左侧),并与y轴相交于点C.(1)、求A、B、C三点的坐标,并求△ABC的面积;(2)、将抛物线L向左或向右平移,得到抛物线L′,且L′与x轴相交于A'、B′两点(点A′在点B′的左侧),并与y轴相交于点C′,要使△A'B′C′和△ABC的面积相等,求所有满足条件的抛物线的函数表达式.22. 如图,在平面直角坐标系中,二次函数y=﹣x2+6x﹣5的图象与x轴交于A、B两点,与y轴交于点C,其顶点为P,连接PA、AC、CP,过点C作y轴的垂线l. (1)、求点P,C的坐标;(2)、直线l上是否存在点Q,使△PBQ的面积等于△PAC的面积的2倍?若存在,求出点Q的坐标;若不存在,请说明理由.23. 抛物线y=ax2+bx的顶点M( ,3)关于x轴的对称点为B,点A为抛物线与x轴的一个交点,点A关于原点O的对称点为A′;已知C为A′B的中点,P为抛物线上一动点,作CD⊥x轴,PE⊥x轴,垂足分别为D,E.
(1)、求点P,C的坐标;(2)、直线l上是否存在点Q,使△PBQ的面积等于△PAC的面积的2倍?若存在,求出点Q的坐标;若不存在,请说明理由.23. 抛物线y=ax2+bx的顶点M( ,3)关于x轴的对称点为B,点A为抛物线与x轴的一个交点,点A关于原点O的对称点为A′;已知C为A′B的中点,P为抛物线上一动点,作CD⊥x轴,PE⊥x轴,垂足分别为D,E. (1)、求点A的坐标及抛物线的解析式;(2)、当0<x<2 时,是否存在点P使以点C,D,P,E为顶点的四边形是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.24. 已知抛物线的顶点为(2,﹣4)并经过点(﹣2,4),点A在抛物线的对称轴上并且纵坐标为﹣ ,抛物线交y轴于点N.如图1.
(1)、求点A的坐标及抛物线的解析式;(2)、当0<x<2 时,是否存在点P使以点C,D,P,E为顶点的四边形是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.24. 已知抛物线的顶点为(2,﹣4)并经过点(﹣2,4),点A在抛物线的对称轴上并且纵坐标为﹣ ,抛物线交y轴于点N.如图1. (1)、求抛物线的解析式;(2)、点P为抛物线对称轴上的一点,△ANP为等腰三角形,求点P的坐标;(3)、如图2,点B为直线y=﹣2上的一个动点,过点B的直线l与AB垂直
(1)、求抛物线的解析式;(2)、点P为抛物线对称轴上的一点,△ANP为等腰三角形,求点P的坐标;(3)、如图2,点B为直线y=﹣2上的一个动点,过点B的直线l与AB垂直①求证:直线l与抛物线总有两个交点;
②设直线1与抛物线交于点C、D(点C在左侧),分别过点C、D作直线y=﹣2的垂线,垂足分别为E、F.求EF的长.