2018-2019学年初中数学华师大版九年级下册第26章《二次函数》章末测试
试卷更新日期:2019-01-15 类型:单元试卷
一、选择题
-
1. 如图所示是一个抛物线形桥拱的示意图,在所给出的平面直角坐标系中,当水位在AB位置时,水面宽度为10m,此时水面到桥拱的距离是4m,则抛物线的函数关系式为( )
 A、y=
A、y=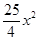 B、y=﹣
B、y=﹣ 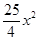 C、y=﹣
C、y=﹣ 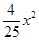 D、y=
D、y= 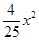 2. 把一根长为50cm的铁丝弯成一个长方形,设这个长方形的一边长为x(cm),它的面积为y(cm2),则y与x之间的函数关系式为( )A、y=﹣x2+50x B、y=x2﹣50x C、y=﹣x2+25x D、y=﹣2x2+253. 二次函数y=kx2+2x+1(k<0)的图象可能是( )A、
2. 把一根长为50cm的铁丝弯成一个长方形,设这个长方形的一边长为x(cm),它的面积为y(cm2),则y与x之间的函数关系式为( )A、y=﹣x2+50x B、y=x2﹣50x C、y=﹣x2+25x D、y=﹣2x2+253. 二次函数y=kx2+2x+1(k<0)的图象可能是( )A、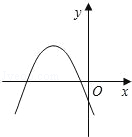 B、
B、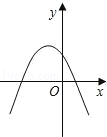 C、
C、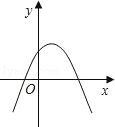 D、
D、 4. 已知抛物线y=ax2+bx+c(a<0)的部分图象如图所示,当y>0时,x的取值范围是( )
4. 已知抛物线y=ax2+bx+c(a<0)的部分图象如图所示,当y>0时,x的取值范围是( ) A、﹣2<x<2 B、﹣4<x<2 C、x<﹣2或x>2 D、x<﹣4或x>25. 抛物线y=x2﹣4x﹣7的顶点坐标是( )A、(2,﹣11) B、(﹣2,7) C、(2,11) D、(2,﹣3)6. 若抛物线y=x2﹣2x+c与y轴的交点为(0,﹣3),则下列说法不正确的是( )A、抛物线开口向上 B、抛物线的对称轴是x=1 C、当x=1时,y的最大值为4 D、抛物线与x轴的交点为(﹣1,0),(3,0)7. 如图,从某建筑物10m高的窗口A处用水管向外喷水,喷出的水成抛物线状(抛物线所在平面与墙面垂直).如果抛物线的最高点M离墙1m,离地面 m,则水流落地点B离墙的距离OB是( )
A、﹣2<x<2 B、﹣4<x<2 C、x<﹣2或x>2 D、x<﹣4或x>25. 抛物线y=x2﹣4x﹣7的顶点坐标是( )A、(2,﹣11) B、(﹣2,7) C、(2,11) D、(2,﹣3)6. 若抛物线y=x2﹣2x+c与y轴的交点为(0,﹣3),则下列说法不正确的是( )A、抛物线开口向上 B、抛物线的对称轴是x=1 C、当x=1时,y的最大值为4 D、抛物线与x轴的交点为(﹣1,0),(3,0)7. 如图,从某建筑物10m高的窗口A处用水管向外喷水,喷出的水成抛物线状(抛物线所在平面与墙面垂直).如果抛物线的最高点M离墙1m,离地面 m,则水流落地点B离墙的距离OB是( ) A、2m B、3m C、4m D、5m8. 如图,有一座抛物线拱桥,当水位在AB位置时,桥拱顶离水面2m,水面宽4m.若水面下降1m,则水面宽CD为( )
A、2m B、3m C、4m D、5m8. 如图,有一座抛物线拱桥,当水位在AB位置时,桥拱顶离水面2m,水面宽4m.若水面下降1m,则水面宽CD为( ) A、5m B、6m C、 m D、2 m
A、5m B、6m C、 m D、2 m二、填空题
-
9.
函数 与 的图象及交点如图所示,则不等式x2<x+2的解集是 .
 10. 如图是二次函数y=ax2+bx+c的部分图象,由图象可知ax2+bx+c>0时x的取值范围是 .
10. 如图是二次函数y=ax2+bx+c的部分图象,由图象可知ax2+bx+c>0时x的取值范围是 . 11. 抛物线y= x2﹣4x+3的顶点坐标和对称轴分别是 .12. 抛物线y=x2﹣(m2﹣3m+2)x+m2﹣4的图象的对称轴是y轴,且顶点在原点,则m的值为 .13. 若抛物线y=ax2+4x+a的顶点的纵坐标是3,则a= .14. 如图,一块草地是长80 m,宽60 m的矩形,欲在中间修筑两条互相垂直的宽为xm的小路,这时草坪面积为y m2 . 求y与x的函数关系式,并写出自变量x的取值.
11. 抛物线y= x2﹣4x+3的顶点坐标和对称轴分别是 .12. 抛物线y=x2﹣(m2﹣3m+2)x+m2﹣4的图象的对称轴是y轴,且顶点在原点,则m的值为 .13. 若抛物线y=ax2+4x+a的顶点的纵坐标是3,则a= .14. 如图,一块草地是长80 m,宽60 m的矩形,欲在中间修筑两条互相垂直的宽为xm的小路,这时草坪面积为y m2 . 求y与x的函数关系式,并写出自变量x的取值.
三、解答题
-
15. 已知正方形的面积为y(cm2),周长为x(cm).(1)、请写出y与x的函数关系式.(2)、判断y是否为x的二次函数.16. 为了改善小区环境,某小区决定要在一块一边靠墙(墙长25m)的空地上修建一条矩形绿化带ABCD,绿化带一边靠墙,另三边用总长为40m的栅栏围住(如图).若设绿化带BC边长为xm,绿化带的面积为ym2 , 求y与x之间的函数关系式,并写出自变量x的取值范围.
 17. 如图所示,在矩形ABCD中,AB=6厘米,BC=12厘米,点P在线段AB上,P从点A开始沿AB边以1厘米/秒的速度向点B移动.点E为线段BC的中点,点Q从E点开始,沿EC以1厘米/秒的速度向点C移动.如果P、Q同时分别从A、E出发,写出出发时间t与△BPQ的面积S的函数关系式,求出t的取值范围.
17. 如图所示,在矩形ABCD中,AB=6厘米,BC=12厘米,点P在线段AB上,P从点A开始沿AB边以1厘米/秒的速度向点B移动.点E为线段BC的中点,点Q从E点开始,沿EC以1厘米/秒的速度向点C移动.如果P、Q同时分别从A、E出发,写出出发时间t与△BPQ的面积S的函数关系式,求出t的取值范围.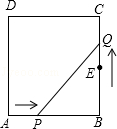 18. 已知抛物线y=ax2+bx+c经过A(0,﹣5),B(1,﹣3),C(﹣1,11)三点,求抛物线的顶点坐标及对称轴.19. 如图,二次函数y=ax2+bx+c的图象经过A、B、C三点.
18. 已知抛物线y=ax2+bx+c经过A(0,﹣5),B(1,﹣3),C(﹣1,11)三点,求抛物线的顶点坐标及对称轴.19. 如图,二次函数y=ax2+bx+c的图象经过A、B、C三点.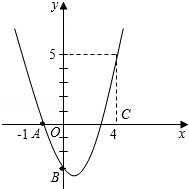 (1)、观察图象,写出A、B、C三点的坐标,并求出抛物线解析式;(2)、求此抛物线的顶点坐标和对称轴;(3)、当m取何值时,ax2+bx+c=m有两个不相等的实数根.20. 已知抛物线的顶点坐标是(2,﹣3),且经过点(1,﹣ ).(1)、求这个抛物线的函数解析式,并作出这个函数的大致图象;(2)、当x在什么范围内时,y随x的增大而增大?当x在什么范围内时,y随x的增大而减小?21. 如图,在平面直角坐标系中,抛物线与x轴交于点A(﹣1,0)和点B(1,0),直线y=2x﹣1与y轴交于点C,与抛物线交于点C、D.求:
(1)、观察图象,写出A、B、C三点的坐标,并求出抛物线解析式;(2)、求此抛物线的顶点坐标和对称轴;(3)、当m取何值时,ax2+bx+c=m有两个不相等的实数根.20. 已知抛物线的顶点坐标是(2,﹣3),且经过点(1,﹣ ).(1)、求这个抛物线的函数解析式,并作出这个函数的大致图象;(2)、当x在什么范围内时,y随x的增大而增大?当x在什么范围内时,y随x的增大而减小?21. 如图,在平面直角坐标系中,抛物线与x轴交于点A(﹣1,0)和点B(1,0),直线y=2x﹣1与y轴交于点C,与抛物线交于点C、D.求: (1)、求抛物线的解析式;(2)、求点D的坐标.22. 根据下列条件求二次函数解析式:(1)、二次函数的图象过点(0,﹣1),对称轴是直线x=﹣1,且二次函数有最大值2.(2)、二次函数的图象过点(5,6),与x轴交于(﹣1,0),(2,0)两点.23. 如图,在平面直角坐标系中,三个小正方形的边长均为1,且正方形的边与坐标轴平行,边DE落在x轴的正半轴上,边AG落在y轴的正半轴上,A、B两点在抛物线y= x2+bx+c上.
(1)、求抛物线的解析式;(2)、求点D的坐标.22. 根据下列条件求二次函数解析式:(1)、二次函数的图象过点(0,﹣1),对称轴是直线x=﹣1,且二次函数有最大值2.(2)、二次函数的图象过点(5,6),与x轴交于(﹣1,0),(2,0)两点.23. 如图,在平面直角坐标系中,三个小正方形的边长均为1,且正方形的边与坐标轴平行,边DE落在x轴的正半轴上,边AG落在y轴的正半轴上,A、B两点在抛物线y= x2+bx+c上. (1)、直接写出点B的坐标;(2)、求抛物线y= x2+bx+c的解析式;(3)、将正方形CDEF沿x轴向右平移,使点F落在抛物线y= x2+bx+c上,求平移的距离.24. 如图,已知二次函数y=﹣ x2+ x+4的图象与y轴交于点A,与x轴交于B、C两点,其对称轴与x轴交于点D,连接AC.
(1)、直接写出点B的坐标;(2)、求抛物线y= x2+bx+c的解析式;(3)、将正方形CDEF沿x轴向右平移,使点F落在抛物线y= x2+bx+c上,求平移的距离.24. 如图,已知二次函数y=﹣ x2+ x+4的图象与y轴交于点A,与x轴交于B、C两点,其对称轴与x轴交于点D,连接AC. (1)、点A的坐标为 , 点C的坐标为;(2)、△ABC是直角三角形吗?若是,请给予证明;(3)、线段AC上是否存在点E,使得△EDC为等腰三角形?若存在,求出所有符合条件的点E的坐标;若不存在,请说明理由.
(1)、点A的坐标为 , 点C的坐标为;(2)、△ABC是直角三角形吗?若是,请给予证明;(3)、线段AC上是否存在点E,使得△EDC为等腰三角形?若存在,求出所有符合条件的点E的坐标;若不存在,请说明理由.