2018-2019学年初中数学华师大版九年级下册26.3.4二次函数综合题 同步练习

试卷更新日期：2019-01-15 类型：同步测试

进入 出卷网 下载

一、选择题

  • 1. 下列函数中，是二次函数的是（   ）
    A、y=8x2+1 B、   y=8x+1 C、   D、

    查看试题解析

  • 2. 二次函数y=2x（x﹣3）的二次项系数与一次项系数的和为（   ）
    A、2 B、﹣2 C、﹣1 D、﹣4

    查看试题解析

  • 3. 如果y=（a﹣1）x2﹣ax+6是关于x的二次函数，则a的取值范围是（　　）

    A、a≠0 B、a≠1 C、a≠1且a≠0 D、无法确定

    查看试题解析

  • 4. 若函数 y=(m−3)xm2−3m+2+mx+1 是二次函数，则m的值一定是（   ）
    A、3 B、0 C、3或0 D、1或2

    查看试题解析

  • 5. 如图，四边形ABCD中，∠BAD=∠ACB=90°，AB=AD，AC=4BC，设CD的长为x，四边形ABCD的面积为y，则y与x之间的函数关系式是（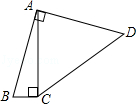  

    A、y=425x2 B、 y=225x2 C、   y=25x2 D、y=45x2

    查看试题解析

  • 6. 图（1）是一个横断面为抛物线形状的拱桥，当水面在l时，拱顶（拱桥洞的最高点）离水面2m，水面宽4m．如图（2）建立平面直角坐标系，则抛物线的关系式是（   ）

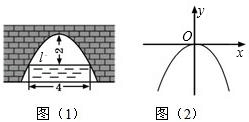    A、y=﹣2x2 B、   y=2x2 C、   y=﹣ x2 D、y= x2

    查看试题解析

  • 7. 进入夏季后，某电器商场为减少库存，对电热取暖器连续进行两次降价．若设平均每次降价的百分率是x，降价后的价格为y元，原价为a元，则y与x之间的函数关系式为（   ）
    A、y=2a（x﹣1） B、y=2a（1﹣x） C、y=a（1﹣x2） D、y=a（1﹣x）2

    查看试题解析

  • 8. 喜迎圣诞，某商店销售一种进价为50元/件的商品，售价为60元/件，每星期可卖出200件，若每件商品的售价每上涨1元，则每星期就会少卖出10件．设每件商品的售价上涨x元（x正整数），每星期销售该商品的利润为y元，则y与x的函数解析式为（   ）
    A、y=﹣10x2+100x+2000 B、y=10x2+100x+2000 C、   y=﹣10x2+200x D、y=﹣10x2﹣100x+2000

    查看试题解析

  • 9.

    如图，正方形ABCD的边长为1，E、F分别是边BC和CD上的动点（不与正方形的顶点重合），不管E、F怎样动，始终保持AE⊥EF．设BE=x，DF=y，则y是x的函数，函数关系式是（　　）

    A、y=x+1  B、y=x﹣1 C、y=x2﹣x+1 D、y=x2﹣x﹣1

    查看试题解析

  • 10.

    在一幅长60cm，宽40cm的矩形风景画的四周镶一条金色纸边，制成一幅矩形挂图，如图所示，如果要使整个挂图的面积是ycm2 ， 设金色纸边的宽度为xcm2 ， 那么y关于x的函数是（　　）


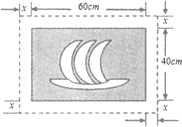    A、y=(60+2x)(40+2x) B、y=(60+x)(40+x) C、y=(60+2x)(40+x) D、y=(60+x)(40+2x)

    查看试题解析

二、填空题（共6小题）

  • 11. 如图，⊙O的半径为2，C1是函数y= 12 x2的图象，C2是函数y=﹣ 12 x2的图象，则阴影部分的面积是 ．

    查看试题解析

  • 12. 已知二次函数y1=ax2+bx+c（a≠0）与一次函数y2=kx+b（k≠0）的图象相交于点A（﹣2，4），B（8，2）（如图所示），则能使y1＞y2成立的x的取值范围是 ．

     

    查看试题解析

  • 13. 如图是二次函数y=a（x+1）2+2图象的一部分，该图在y轴右侧与x轴交点的坐标是 ．

    查看试题解析

  • 14. 请写出一个开口向上，并且与y轴交于点（0，1）的抛物线的解析式，y= ．

    查看试题解析

  • 15. 在平面直角坐标系中，点A是抛物线y=a（x﹣3）2+k与y轴的交点，点B是这条抛物线上的另一点，且AB∥x轴，则以AB为边的等边三角形ABC的周长为 ．

    查看试题解析

  • 16. 已知二次函数y=（x﹣2a）2+（a﹣1）（a为常数），当a取不同的值时，其图象构成一个“抛物线系”．如图分别是当a=﹣1，a=0，a=1，a=2时二次函数的图象．它们的顶点在一条直线上，这条直线的解析式是y=

    查看试题解析

三、解答题

  • 17. 已知抛物线y=a（x﹣3）2+2经过点（1，﹣2）．
    (1)、求a的值；
    (2)、若点A（m，y1）、B（n，y2）（m＜n＜3）都在该抛物线上，试比较y1与y2的大小．

    查看试题解析

  • 18. 若二次函数y=﹣x2图象平移后得到二次函数y=﹣（x﹣2）2+4的图象．

    (1)、平移的规律是：先向（填“左”或“右”）平移个单位，再向平移个单位．

    (2)、在所给的坐标系内画出二次函数y=﹣（x﹣2）2+4的示意图．

    查看试题解析

  • 19. 如图，抛物线y=a（x﹣1）2+4与x轴交于点A，B，与y轴交于点C，过点C作CD∥x轴交抛物线的对称轴于点D，连接BD，已知点A的坐标为（﹣1，0）

    (1)、求该抛物线的解析式；
    (2)、求梯形COBD的面积．

    查看试题解析

  • 20.

    如图，抛物线y=a（x﹣h）2+k经过点A（0，1），且顶点坐标为B（1，2），它的对称轴与x轴交于点C．

    (1)、求此抛物线的解析式．

    (2)、在第一象限内的抛物线上求点P，使得△ACP是以AC为底的等腰三角形，请求出此时点P的坐标．

    (3)、上述点是否是第一象限内此抛物线上与AC距离最远的点？若是，请说明理由；若不是，请求出第一象限内此抛物线上与AC距离最远的点的坐标．

    查看试题解析