2018-2019学年初中数学华师大版九年级下册26.3.2二次函数与不等式（组） 同步练习
试卷更新日期：2019-01-15 类型：同步测试
一、选择题
-
1. 已知二次函数y=ax2+bx+c的y与x的部分对应值如下表：则下列判断中正确的是（ ）
A、抛物线开口向上 B、抛物线与y轴交于负半轴 C、当x=3时，y＜0 D、方程ax2+bx+c=0有两个相等实数根2.如图，已知二次函数y=ax2+bx+c的部分图象，由图象可知关于x的一元二次方程ax2+bx+c=0的两个根分别是x1=1.6，x2=（ ）
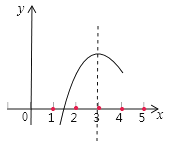A、﹣1.6 B、3.2 C、4.4 D、以上都不对3. 二次函数y=ax2+bx+c（a≠0）的函数值y与自变量x的四组对应值如表所示x
6.15
6.18
6.21
6.24
y
0.02
-0.01
0.02
0.11
则方程ax2+bx+c=0的根的个数是（ ）
A、0 B、1 C、2 D、不能确定4.如图，以（1，﹣4）为顶点的二次函数y=ax2+bx+c的图象与x轴负半轴交于A点，则一元二次方程ax2+bx+c=0的正数解的范围是（ ）
A、2＜x＜3 B、3＜x＜4 C、4＜x＜5 D、5＜x＜65. 二次函数y=ax2+bx+c（a≠0）的图象如图所示，则函数值y＞0时，x的取值范围是（ ）
A、x＜﹣1 B、x＞3 C、﹣1＜x＜3 D、x＜﹣1或x＞36. 如图是二次函数y=﹣x2+2x+4的图象，使y≤1成立的x的取值范围是（ ）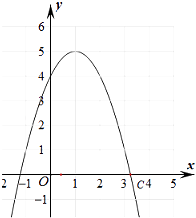
A、﹣1≤x≤3 B、x≤﹣1 C、x≥1 D、x≤﹣1或x≥37. 二次函数y=x2+bx的图象如图，对称轴为直线x=1，若关于x的一元二次方程x2+bx﹣t=0（t为实数）在﹣1＜x＜4的范围内有解，则t的取值范围是（ ）
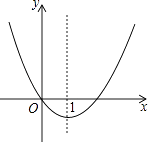A、t≥﹣1 B、﹣1≤t＜3 C、﹣1≤t＜8 D、3＜t＜88. 如图，已知二次函数y=﹣x2+2x，当﹣1＜x＜a时，y随x的增大而增大，则实数a的取值范围是（ ）
A、a＞1 B、﹣1＜a≤1 C、a＞0 D、﹣1＜a＜2二、填空题（共6小题）
-
9. 如图，是二次函数y=ax2+bx+c图象的一部分，其对称轴为直线x=1，若其与x轴一交点为A（3，0），则由图象可知，不等式ax2+bx+c＜0的解集是 ．
10. 抛物线y=x2+1与双曲线y= 的交点A的横坐标是1，则关于x的不等式﹣ +x2+1＜0的解集是 ．
11. 根据如图的函数图象，可得不等式ax2+bx+c＜ 的解集为 ．
12. 如图是函数y=x2+bx﹣1的图象，根据图象提供的信息，确定使﹣1≤y≤2的自变量x的取值范围是 ．
13. 如图，抛物线y=ax2+bx与直线y=kx相交于O（0，0）和A（3，2）两点，则不等式ax2+bx＜kx的解集为 ．
14. 如图，是y=x2、y=x、y= 在同一直角坐标系中图象，请根据图象写出 ＜x＜x2时x的取值范围是 ．
三、解答题
-
15. 先阅读理解下面的例题，再按要求解答后面的问题
例题：解一元二次不等式x2﹣3x+2＞0．
解：令y=x2﹣3x+2，画出y=x2﹣3x+2如图所示，由图象可知：当x＜1或x＞2时，y＞0．所以一元二次不等式x2﹣3x+2＞0的解集为x＜1或x＞2．
填空：
(1)、x2﹣3x+2＜0的解集为；(2)、x2﹣1＞0的解集为；用类似的方法解一元二次不等式﹣x2﹣5x+6＞0．
16. 如图，直线y=x+m和抛物线y=x2+bx+c都经过点A（1，0），B（3，2）．
(1)、求m的值和抛物线的解析式；(2)、求不等式x2+bx+c＞x+m的解集．（直接写出答案）17. 已知函数y1=a（x﹣h）2与y2=kx+b的图象交于A、B两点，其中A（0，﹣1），B（1，0）．(1)、求出y1与y2的解析式；(2)、根据图象，说出当x取什么值时，y1＞y2 ．18. 如图，抛物线y=x2+1与双曲线y= 的交点A的横坐标是1，
(1)、求k的值；(2)、根据图象，写出关于x的不等式 ﹣x2﹣1＜0的解集．
