2018-2019学年初中数学华师大版九年级下册26.2.1二次函数y=ax²的图像与性质 同步练习
试卷更新日期:2019-01-15 类型:同步测试
一、选择题
-
1. 已知反比例函数y= (a≠0),当x>0时,它的图象y随x的增大而减小,那么二次函数y=ax2﹣ax的图象只可能是( )A、
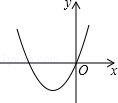 B、
B、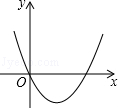 C、
C、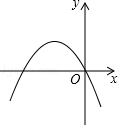 D、
D、 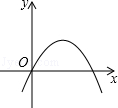 2. 已知a≠0,在同一直角坐标系中,函数y=ax与y=ax2的图象有可能是( )A、
2. 已知a≠0,在同一直角坐标系中,函数y=ax与y=ax2的图象有可能是( )A、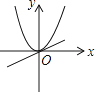 B、
B、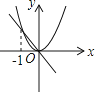 C、
C、 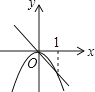 D、
D、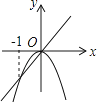 3. 函数y=ax2+1与y= (a≠0)在同一平面直角坐标系中的图象可能是( )
3. 函数y=ax2+1与y= (a≠0)在同一平面直角坐标系中的图象可能是( )
A、 B、
B、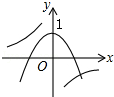 C、
C、 D、
D、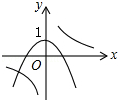 4. 已知抛物线y=ax2+bx和直线y=ax+b在同一坐标系内的图象如图,其中正确的是( )A、
4. 已知抛物线y=ax2+bx和直线y=ax+b在同一坐标系内的图象如图,其中正确的是( )A、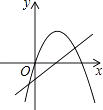 B、
B、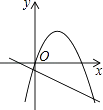 C、
C、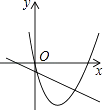 D、
D、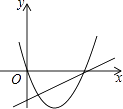 5. 已知函数y=﹣(x﹣m)(x﹣n)(其中m<n)的图象如图所示,则一次函数y=mx+n与反比例函数y=的图象可能是( )
5. 已知函数y=﹣(x﹣m)(x﹣n)(其中m<n)的图象如图所示,则一次函数y=mx+n与反比例函数y=的图象可能是( )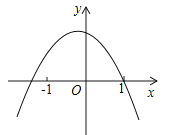 A、
A、 B、
B、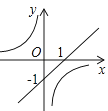 C、
C、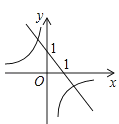 D、
D、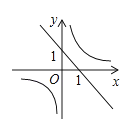 6. 函数y= 与y=ax2(a≠0)在同一平面直角坐标系中的图象可能是( )A、
6. 函数y= 与y=ax2(a≠0)在同一平面直角坐标系中的图象可能是( )A、 B、
B、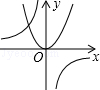 C、
C、 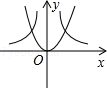 D、
D、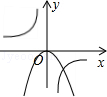 7. 二次函数y=ax2+b(b>0)与反比例函数 y= 在同一坐标系中的图象可能是( )
7. 二次函数y=ax2+b(b>0)与反比例函数 y= 在同一坐标系中的图象可能是( )
A、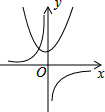 B、
B、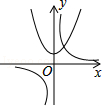 C、
C、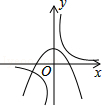 D、
D、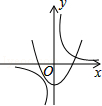 8. 已知二次函数y=ax2+bx+c(a , b , c是常数,且a≠0)的图象如图所示,则一次函数y=cx+ 与反比例函数 在同一坐标系内的大致图象是( )
8. 已知二次函数y=ax2+bx+c(a , b , c是常数,且a≠0)的图象如图所示,则一次函数y=cx+ 与反比例函数 在同一坐标系内的大致图象是( )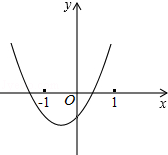 A、
A、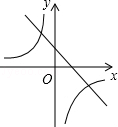 B、
B、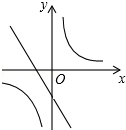 C、
C、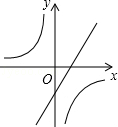 D、
D、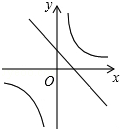
二、填空题
-
9. 下列函数中,当x>0时y随x的增大而减小的有 .
( 1 )y=﹣x+1,(2)y=2x,(3) ,(4)y=﹣x2 .
10. 如图,抛物线与两坐标轴的交点坐标分别为(﹣1,0),(2,0),(0,2),则抛物线的对称轴是;若y>2,则自变量x的取值范围是 .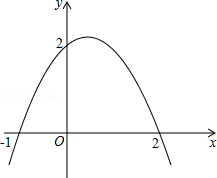 11. 抛物线y=﹣x2+bx+c的部分图象如图所示,若y>0,则x的取值范围是 .
11. 抛物线y=﹣x2+bx+c的部分图象如图所示,若y>0,则x的取值范围是 .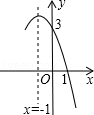 12. 如图,边长为2的正方形ABCD的中心在直角坐标系的原点O,AD∥x轴,以O为顶点且过A、D两点的抛物线与以O为顶点且过B、C两点的抛物线将正方形分割成几部分.则图中阴影部分的面积是 .
12. 如图,边长为2的正方形ABCD的中心在直角坐标系的原点O,AD∥x轴,以O为顶点且过A、D两点的抛物线与以O为顶点且过B、C两点的抛物线将正方形分割成几部分.则图中阴影部分的面积是 .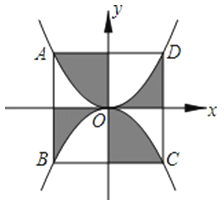 13. 如图,⊙O的半径为2.C1是函数y=x2的图象,C2是函数y=﹣x2的图象,则阴影部分的面积是 .
13. 如图,⊙O的半径为2.C1是函数y=x2的图象,C2是函数y=﹣x2的图象,则阴影部分的面积是 .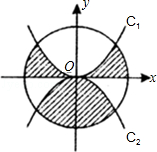 14.
14.已知抛物线y=ax2+bx+c的部分图象如图所示,若y>0,则x的取值范围是 .
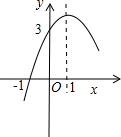
三、解答题
-
15. 抛物线y=﹣x2+(m﹣1)x+m与y轴交于(0,3)点.
 (1)、求出m的值并画出这条抛物线;(2)、求它与x轴的交点和抛物线顶点的坐标;(3)、x取什么值时,抛物线在x轴上方?(4)、x取什么值时,y的值随x值的增大而减小?16. 已知二次函数y=ax2+bx+c的图象如图所示:
(1)、求出m的值并画出这条抛物线;(2)、求它与x轴的交点和抛物线顶点的坐标;(3)、x取什么值时,抛物线在x轴上方?(4)、x取什么值时,y的值随x值的增大而减小?16. 已知二次函数y=ax2+bx+c的图象如图所示: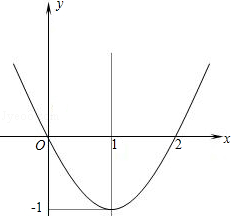 (1)、这个二次函数的解析式是y=;(2)、当x=时,y=3;(3)、根据图象回答:当x时,y>0.17. 分别在同一直角坐标系内,描点画出y= x2+3与y= x2的二次函数的图象,并写出它们的对称轴与顶点坐标.
(1)、这个二次函数的解析式是y=;(2)、当x=时,y=3;(3)、根据图象回答:当x时,y>0.17. 分别在同一直角坐标系内,描点画出y= x2+3与y= x2的二次函数的图象,并写出它们的对称轴与顶点坐标.