2018-2019学年初中数学华师大版七年级下册第7章一次方程组 单元检测提高卷
试卷更新日期:2019-01-15 类型:单元试卷
一、选择题
-
1. 如果2xa﹣2b﹣3ya+b+1=0是二元一次方程,那么a,b的值分别是( )A、1,0 B、0,1 C、﹣1,2 D、2,﹣12. 方程2x+3y=15的正整数解有( )A、0个 B、1个 C、2个 D、无数个3. 小明只带2元和5元两种面值的人民币,他买一件学习用品要支付23元,则付款的方式有( )A、1种 B、2种 C、3种 D、4种4. 下列方程组是二元一次方程组的是( )A、
 B、
B、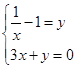 C、
C、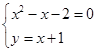 D、
D、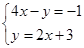 5. 已知 是二元一次方程组 的解,则2m﹣n的算术平方根是( )A、4 B、2 C、 D、±26. 对于非零的两个实数a,b,规定a⊕b=am﹣bn,若3⊕(﹣5)=15,4⊕(﹣7)=28,则(﹣1)⊕2的值为( )A、﹣13 B、13 C、2 D、﹣27. 如果方程组 与 有相同的解,则a,b的值是( )A、
5. 已知 是二元一次方程组 的解,则2m﹣n的算术平方根是( )A、4 B、2 C、 D、±26. 对于非零的两个实数a,b,规定a⊕b=am﹣bn,若3⊕(﹣5)=15,4⊕(﹣7)=28,则(﹣1)⊕2的值为( )A、﹣13 B、13 C、2 D、﹣27. 如果方程组 与 有相同的解,则a,b的值是( )A、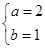 B、
B、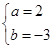 C、
C、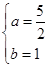 D、
D、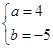 8. 若二元一次方程组 的解也是二元一次方程3x﹣4y=6的解,则k的值为( )A、4 B、8 C、6 D、﹣69. 一张方桌由1个桌面,4个桌腿组成.如果1立方米木料可以做方桌的桌面50个或桌腿300条,现有5立方米木料.那么用多少立方米木料做桌面,多少立方米木料做桌腿做出的桌面和桌腿能恰好配成方桌?设生产桌面、桌腿的木料分别是x、y立方米,则符合题意的方程是( )A、50x+300y=1 B、50x+300 y=5 C、50x=1200y D、200x=300y10. 用白铁皮做罐头盒,每张铁皮可制盒身25个,或制盒底40个,一个盒身与两个盒底配成一套罐头盒.现在又有36张白铁皮.设用x张制作盒身,y张制作盒底可以使盒身和盒底正好配套,则所列方程组正确的( )A、
8. 若二元一次方程组 的解也是二元一次方程3x﹣4y=6的解,则k的值为( )A、4 B、8 C、6 D、﹣69. 一张方桌由1个桌面,4个桌腿组成.如果1立方米木料可以做方桌的桌面50个或桌腿300条,现有5立方米木料.那么用多少立方米木料做桌面,多少立方米木料做桌腿做出的桌面和桌腿能恰好配成方桌?设生产桌面、桌腿的木料分别是x、y立方米,则符合题意的方程是( )A、50x+300y=1 B、50x+300 y=5 C、50x=1200y D、200x=300y10. 用白铁皮做罐头盒,每张铁皮可制盒身25个,或制盒底40个,一个盒身与两个盒底配成一套罐头盒.现在又有36张白铁皮.设用x张制作盒身,y张制作盒底可以使盒身和盒底正好配套,则所列方程组正确的( )A、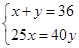 B、
B、 C、
C、 D、
D、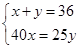 11. 如图所示,小刚手拿20元钱正在和售货员对话,请你仔细看图,1听果奶、1听可乐的单价分别是( )
11. 如图所示,小刚手拿20元钱正在和售货员对话,请你仔细看图,1听果奶、1听可乐的单价分别是( ) A、3元,3.5元 B、3.5元,3元 C、4元,4.5元 D、4.5元,4元12. 滴滴快车是一种便捷的出行工具,计价规则如下表:
A、3元,3.5元 B、3.5元,3元 C、4元,4.5元 D、4.5元,4元12. 滴滴快车是一种便捷的出行工具,计价规则如下表:计费项目
里程费
时长费
远途费
单价
1.8元/公里
0.3元/分钟
0.8元/公里
注:车费由里程费、时长费、远途费三部分构成,其中里程费按行车的实际里程计算;时长费按行车的实际时间计算;远途费的收取方式为:行车里程7公里以内(含7公里)不收远途费,超过7公里的,超出部分每公里收0.8元.
小王与小张各自乘坐滴滴快车,行车里程分别为6公里与8.5公里.如果下车时两人所付车费相同,那么这两辆滴滴快车的行车时间相差( )
A、10分钟 B、13分钟 C、15分钟 D、19分钟二、填空题
-
13. 是二元一次方程ax+by=11的一组解,则2017﹣2a+b= .14. 若方程组 是关于x,y的二元一次方程组,则代数式a+b+c的值是 .15. 三个同学对问题“若方程组的 解是 ,求方程组 的解.”提出各自的想法.甲说:“这个题目好象条件不够,不能求解”;乙说:“它们的系数有一定的规律,可以试试”;丙说:“能不能把第二个方程组的两个方程的两边都除以5,通过换元替换的方法来解决”.参考他们的讨论,你认为这个题目的解应该是 .16. 解方程组 ,小明正确解得 ,小丽只看错了c解得 ,则当x=﹣1时,代数式ax2﹣bx+c的值为 .17. 若二元一次方程组 和 同解,则可通过解方程组求得这个解.18. 已知a、b、c满足 ,则a= , b= , c= .
三、解答题
-
19. 解方程组:(1)、(2)、 .20. 关于x,y的方程组(1)、若x的值比y的值小5,求m的值;(2)、若方程3x+2y=17与方程组的解相同,求m的值.21. 已知关于x,y的方程组 的解满足x+y=2k.(1)、求k的值;(2)、试判断该方程组的解是否也是方程组 的解.22. 某专卖店有 , 两种商品.已知在打折前,买60件 商品和30件 商品用了1080元,买50件 商品和10件 商品用了840元; , 两种商品打相同折以后,某人买500件 商品和450件 商品一共比不打折少花1960元,计算打了多少折?23. 小明作业本中有一页被墨水污染了,已知他所列的方程组是正确的.写出题中被墨水污染的条件,并求解这道应用题.
 24. 学校“百变魔方”社团准备购买A,B两种魔方,已知购买2个A种魔方和6个B种魔方共需130元,购买3个A种魔方和4个B种魔方所需款数相同.
24. 学校“百变魔方”社团准备购买A,B两种魔方,已知购买2个A种魔方和6个B种魔方共需130元,购买3个A种魔方和4个B种魔方所需款数相同. (1)、求这两种魔方的单价;(2)、结合社员们的需求,社团决定购买A,B两种魔方共100个(其中A种魔方不超过50个).某商店有两种优惠活动,如图所示.请根据以上信息,说明选择哪种优惠活动购买魔方更实惠.25. 某汽车制造厂开发一款新式电动汽车,计划一年生产安装240辆.由于抽调不出足够的熟练工来完成新式电动汽车的安装,工厂决定招聘一些新工人.他们经过培训后上岗,也能独立进行电动汽车的安装.生产开始后,调研部门发现:1名熟练工和2名新工人每月可安装8辆电动汽车;2名熟练工和3名新工人每月可安装14辆电动汽车.(1)、每名熟练工和新工人每月分别可以安装多少辆电动汽车?(2)、如果工厂招聘n(0<n<10)名新工人,使得招聘的新工人和抽调的熟练工刚好能完成一年的安装任务,那么工厂有哪几种新工人的招聘方案?26. “全民阅读”深入人心,好读书,读好书,让人终身受益.我校上月举办了“读书节”活动.为了表彰优秀,主办单位王老师负责购买奖品.他发现:若以2支钢笔和3本笔记本为一份奖品,则可买60份奖品;若以2支钢笔和6本笔记本为一份奖品,则可以买40份奖品.设钢笔单价为x元/支,笔记本单价为y元/本.(1)、请用x的代数式表示y.(2)、若用这钱全部购买笔记本,总共可以买几本?(3)、若王老师用这钱恰好买30份同样的奖品,可以选择a支钢笔和b本笔记本作为一份奖品(两种奖品都要有),请求出所有可能的a、b值.27. 为了解决农民工子女入学难的问题.我市建立了一套进城农民工子女就学保障机制,其中一项就是免交“借读费”.据统计,2017年秋季有5000名农民工子女进入主城区中小学学习,预测2018年秋季进入主城区中小学学习的农民工子女将比2017年有所增加,其中小学增加20%,中学增加30%,这样,2018年秋季将新增1200名农民工子女在主城区中小学学习.(1)、2017年秋季农民工子女进入主城区中小学学习的小学生、中学生各有多少名?(2)、如果按小学每生每年收“借读费“600元,中学每生每年收“借读费”800元计算,求2018年新增的1200名中小学生共免收多少“借读费”?(3)、如果小学每40名学生配备2名教师,中学每40名学生配备3名教师,若按2018年秋季入学后,农民工子女在主城区中小学就读的学生人数计算,一共需要配备多少名中小学教师?
(1)、求这两种魔方的单价;(2)、结合社员们的需求,社团决定购买A,B两种魔方共100个(其中A种魔方不超过50个).某商店有两种优惠活动,如图所示.请根据以上信息,说明选择哪种优惠活动购买魔方更实惠.25. 某汽车制造厂开发一款新式电动汽车,计划一年生产安装240辆.由于抽调不出足够的熟练工来完成新式电动汽车的安装,工厂决定招聘一些新工人.他们经过培训后上岗,也能独立进行电动汽车的安装.生产开始后,调研部门发现:1名熟练工和2名新工人每月可安装8辆电动汽车;2名熟练工和3名新工人每月可安装14辆电动汽车.(1)、每名熟练工和新工人每月分别可以安装多少辆电动汽车?(2)、如果工厂招聘n(0<n<10)名新工人,使得招聘的新工人和抽调的熟练工刚好能完成一年的安装任务,那么工厂有哪几种新工人的招聘方案?26. “全民阅读”深入人心,好读书,读好书,让人终身受益.我校上月举办了“读书节”活动.为了表彰优秀,主办单位王老师负责购买奖品.他发现:若以2支钢笔和3本笔记本为一份奖品,则可买60份奖品;若以2支钢笔和6本笔记本为一份奖品,则可以买40份奖品.设钢笔单价为x元/支,笔记本单价为y元/本.(1)、请用x的代数式表示y.(2)、若用这钱全部购买笔记本,总共可以买几本?(3)、若王老师用这钱恰好买30份同样的奖品,可以选择a支钢笔和b本笔记本作为一份奖品(两种奖品都要有),请求出所有可能的a、b值.27. 为了解决农民工子女入学难的问题.我市建立了一套进城农民工子女就学保障机制,其中一项就是免交“借读费”.据统计,2017年秋季有5000名农民工子女进入主城区中小学学习,预测2018年秋季进入主城区中小学学习的农民工子女将比2017年有所增加,其中小学增加20%,中学增加30%,这样,2018年秋季将新增1200名农民工子女在主城区中小学学习.(1)、2017年秋季农民工子女进入主城区中小学学习的小学生、中学生各有多少名?(2)、如果按小学每生每年收“借读费“600元,中学每生每年收“借读费”800元计算,求2018年新增的1200名中小学生共免收多少“借读费”?(3)、如果小学每40名学生配备2名教师,中学每40名学生配备3名教师,若按2018年秋季入学后,农民工子女在主城区中小学就读的学生人数计算,一共需要配备多少名中小学教师?