2018-2019学年初中数学华师大版七年级下册第6章一元一次方程 单元检测基础卷
试卷更新日期:2019-01-15 类型:单元试卷
一、选择题
-
1. 若关于x的方程mxm﹣2﹣m+3=0是一元一次方程,则这个方程的解是( )A、x=0 B、x=3 C、x=﹣3 D、x=22. 把方程x=1变形为x=2,其依据是( )A、等式的性质1 B、等式的性质2 C、分式的基本性质 D、不等式的性质13. 下列运用等式的性质对等式进行的变形中,正确的是( ).A、若
 ,则
,则  B、若
B、若 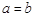 ,则
,则 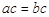 C、若
C、若  ,则
,则  D、若
D、若  ,则
,则 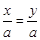 4. 把方程 去分母后,正确的是( )A、3x﹣2(x﹣1)=1 B、3x﹣2(x﹣1)=6 C、3x﹣2x﹣2=6 D、3x+2x﹣2=65. 下面是一个被墨水污染过的方程:
4. 把方程 去分母后,正确的是( )A、3x﹣2(x﹣1)=1 B、3x﹣2(x﹣1)=6 C、3x﹣2x﹣2=6 D、3x+2x﹣2=65. 下面是一个被墨水污染过的方程: ,答案显示此方程的解是x=-1,被墨水遮盖的是一个常数,则这个常数是( ) A、1 B、-1 C、 D、
,答案显示此方程的解是x=-1,被墨水遮盖的是一个常数,则这个常数是( ) A、1 B、-1 C、 D、 6. 小明准备为希望工程捐款,他现在有20元,以后每月打算存10元.若设x月后他能捐出100元,则下列方程中能正确计算出x的是( )
6. 小明准备为希望工程捐款,他现在有20元,以后每月打算存10元.若设x月后他能捐出100元,则下列方程中能正确计算出x的是( )
A、10x+20=100 B、10x-20=100 C、20-10x=100 D、20x+10=1007. 某商店把一商品按标价的九折出售(即优惠10%),仍可获利20%,若该商品的标价为每件28元,则该商品的进价为( )A、21元 B、19.8元 C、22.4元 D、25.2元8. 甲、乙二人按2:5的比例投资开办了一家公司,约定除去各项开支外,所得利润按投资比例分成.若第一年赢得14000元,那么甲、乙二人分别应分得( )A、2000元,5000元 B、5000元,2000元 C、4000元,10000元 D、10000元,4000元9. 一个两位数的个位数字与十位数字都是,如果将个位数字与十位数字分别加2和1,所得新数比原数大12,则可列的方程是( )A、2x+3=12 B、10x+2+3=12 C、(10x+x)-10(x+1)-(x+2)=12 D、10(x+1)+(x+2)=10x+x+1210.在矩形ABCD中放入六个长、宽都相同的小长方形,所标尺寸如图所示,求小长方形的宽AE.若AE=x(cm),依题意可得方程( )
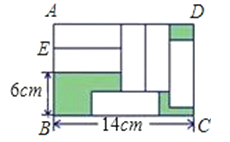 A、6+2x=14﹣3x B、6+2x=x+(14﹣3x) C、14﹣3x=6 D、6+2x=14﹣x
A、6+2x=14﹣3x B、6+2x=x+(14﹣3x) C、14﹣3x=6 D、6+2x=14﹣x二、填空题
-
11. 已知关于x的方程 =4的解是x=4,则a= .12. 方程2x+3=4和方程3x+1=k有相同的解,则k= .13. 五•一期间,某商场推出全场打八折的优惠活动,持贵宾卡可在八折基础上继续打折,小明妈妈持贵宾卡买了标价为10000元的商品,共节省2800元,则用贵宾卡又享受了折优惠.14. 有m辆客车及n个人,若每辆客车乘40人,则还有10人不能上车;若每辆客车乘43人,则最后一辆车有2个空位.给出下面五个等式:①40m+10=43m﹣2;②40m﹣10=43m+2;③ = ;④ = ;⑤43m=n+2.其中正确的是(只填序号).15. 一个学生由于粗心,在计算 的值时,误将“ ”看成“ ”,结果得21,则 的值应为。
三、解答题
-
16. 当n为何值时,关于x的方程 的解为0?17. 解方程:(1)、2(3y﹣1)=7(y﹣2)+3;(2)、 ﹣1= .18. 依据下列解方程 的过程,请在前面的括号内填写变形步骤,在后面的括号内填写变形依据.
解:原方程可变形为 ( )
去分母,得3(3x+5)=2(2x﹣1).( )
去括号,得9x+15=4x﹣2.( )
( ),得9x﹣4x=﹣15﹣2.( )
合并,得5x=﹣17.( )
( ),得x= .( )
19. 如果方程 的解与方程4x﹣(3a+1)=6x+2a﹣1的解相同,求式子 的值.20. 一家商店将某种服装按成本价提高40%标价,又以8折优惠卖出,结果每件仍获利15元,这种服装每件的成本多少元?21. 甲、乙两站相距560千米,一列慢车从甲站开出,每小时行驶48千米,一列快车从乙站开出,每小时行驶72千米,快车先开出25分钟,两车相向出行,慢车行驶多少小时后两车相遇?22. 3个工程队合修一条公路,第一工程队修全路的 ,第二工程队修剩下的 ,第三工程队修了20千米把这条公路修完.这条公路共有多少千米?23. 如图,是一个时钟,过它的中心点O可以画两条相互垂直的直线,使得这两条直线经过钟面上表示时间的四个数字。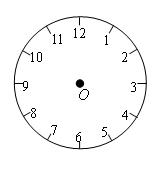 (1)、请你在图中画出符合条件的两条相互垂直的直线即可。(2)、若这四个数字的和是22,求出这四个数字中最小的一个数字。24. 大数学家孙子在《孙子算经》中记载了这样的一道题:“今有雏兔同笼,上有三十五头,下有九十四足,问雏兔各几何?”这四句话的意思就是:有若干只鸡和兔在同一个笼子里,从上面数,有三十五个头;从下面数,有九十四只脚.求笼中各有几只鸡和兔?
(1)、请你在图中画出符合条件的两条相互垂直的直线即可。(2)、若这四个数字的和是22,求出这四个数字中最小的一个数字。24. 大数学家孙子在《孙子算经》中记载了这样的一道题:“今有雏兔同笼,上有三十五头,下有九十四足,问雏兔各几何?”这四句话的意思就是:有若干只鸡和兔在同一个笼子里,从上面数,有三十五个头;从下面数,有九十四只脚.求笼中各有几只鸡和兔?原来孙子提出了大胆的设想,他假设砍去每只鸡、每只兔一半的脚,则每只鸡就变成了“独脚鸡”,而每只免就变成了“双脚免”,这样,“独脚鸡”和“双脚免”的脚就由94只变成了47只;而每只“鸡”的头数与脚数之比变为1:1,每只“兔”的头数与脚数之比变为1:2.由此可知,有一只“双脚兔”,脚的数量就会比头的数量多1.所以,“独脚鸡”和“双脚兔”的脚的数量与他们的头的数量之差,就是兔子的只数,即:47﹣35=12(只);鸡的数量就是35﹣12=23(只).当然,这道题还可以用方程来解答,请同学们用方程的思想解答此题.
25. 为发展校园足球运动,某县城区四校决定联合购买一批足球运动装备,市场调查发现:甲、乙两商场以同样的价格出售同种品牌的足球队服和足球,已知每套队服比每个足球多50元,两套队服与三个足球的费用相等,经洽谈,甲商场优惠方案是:每购买十套队服,送一个足球;乙商场优惠方案是:若购买队服超过80套,则购买足球打八折.(1)、求每套队服和每个足球的价格是多少?(2)、若城区四校联合购买100套队服和a个足球,请用含a的式子分别表示出到甲商场和乙商场购买装备所花的费用;(3)、假如你是本次购买任务的负责人,你认为到哪家商场购买比较合算?