2018-2019学年初中数学华师大版七年级下册7.2二元一次方程组的解法(3)同步练习
试卷更新日期:2019-01-15 类型:同步测试
一、选择题
-
1. 甲乙两人在相距18千米的两地,若同时出发相向而行,经2小时相遇;若同向而行,且甲比乙先出发1小时追及乙,那么在乙出发后经4小时两人相遇,求甲、乙两人的速度.设甲的速度为x千米/小时,乙的速度为y千米/小时,则可列方程组为( )A、
 B、
B、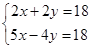 C、
C、 D、
D、 2. 已知两数x、y之和是10,x比y的2倍大1,则下面所列方程组正确的是( )A、
2. 已知两数x、y之和是10,x比y的2倍大1,则下面所列方程组正确的是( )A、 B、
B、  C、
C、  D、
D、  3. 端午节时,王老师用72元钱买了荷包和五彩绳共20个,其中荷包每个4元,五彩绳每个3元.设王老师购买荷包x个,五彩绳y个,根据题意,下面列出的方程组正确的是( )A、
3. 端午节时,王老师用72元钱买了荷包和五彩绳共20个,其中荷包每个4元,五彩绳每个3元.设王老师购买荷包x个,五彩绳y个,根据题意,下面列出的方程组正确的是( )A、 B、
B、 C、
C、 D、
D、 4. “珍爱生命,拒绝毒品”,学校举行的2017年禁毒知识竞赛共有60道题,曾浩同学答对了x道题,答错了y道题(不答视为答错),且答对题数比答错题数的7倍还多4道,那么下面列出的方程组中正确的是( )A、
4. “珍爱生命,拒绝毒品”,学校举行的2017年禁毒知识竞赛共有60道题,曾浩同学答对了x道题,答错了y道题(不答视为答错),且答对题数比答错题数的7倍还多4道,那么下面列出的方程组中正确的是( )A、 B、
B、  C、
C、  D、
D、  5. 如图,设他们中有x个成人,y个儿童.根据图中的对话可得方程组( )
5. 如图,设他们中有x个成人,y个儿童.根据图中的对话可得方程组( ) A、
A、 B、
B、 C、
C、 D、
D、 6. 小明在某商店购买商品A,B共两次,这两次购买商品A,B的数量和费用如下表:
6. 小明在某商店购买商品A,B共两次,这两次购买商品A,B的数量和费用如下表:购买商品A的数量/个
购买商品B的数量/个
购买总费用/元
第一次购物
4
3
93
第二次购物
6
6
162
若小丽需要购买3个商品A和2个商品B,则她要花费( )
A、64元 B、65元 C、66元 D、67元7. 某单位组织34人分别到井冈山和瑞金进行革命传统教育,到井冈山的人数是到瑞金的人数的2倍多1人,求到两地的人数各是多少?设到井冈山的人数为x人,到瑞金的人数为y人.下面所列的方程组正确的是( )A、 B、
B、 C、
C、 D、
D、 8. 养牛场有30头大牛和15头小牛,1天用饲料675kg,一周后又购进12头大牛和5头小牛,这时1天用饲料940kg. 饲养员李大叔估计每头大牛需饲料18至21 kg,每头小牛需6至8 kg. 关于李大叔的估计,下列结论正确的是( )A、大牛每天所需饲料在估计的范围内,小牛每天所需饲料也在估计的范围内 B、大牛每天所需饲料在估计的范围内,小牛每天所需饲料在估计的范围外 C、大牛每天所需饲料在估计的范围外,小牛每天所需饲料在估计的范围内 D、大牛每天所需饲料在估计的范围外,小牛每天所需饲料也在估计的范围外9. 用如图①中的长方形和正方形纸板作侧面和底面,做成如图②的竖式和横式的两种无盖纸盒。现在仓库里有m张正方形纸板和n张长方形纸板,如果做两种纸盒若干个,恰好使库存的纸板用完,则
8. 养牛场有30头大牛和15头小牛,1天用饲料675kg,一周后又购进12头大牛和5头小牛,这时1天用饲料940kg. 饲养员李大叔估计每头大牛需饲料18至21 kg,每头小牛需6至8 kg. 关于李大叔的估计,下列结论正确的是( )A、大牛每天所需饲料在估计的范围内,小牛每天所需饲料也在估计的范围内 B、大牛每天所需饲料在估计的范围内,小牛每天所需饲料在估计的范围外 C、大牛每天所需饲料在估计的范围外,小牛每天所需饲料在估计的范围内 D、大牛每天所需饲料在估计的范围外,小牛每天所需饲料也在估计的范围外9. 用如图①中的长方形和正方形纸板作侧面和底面,做成如图②的竖式和横式的两种无盖纸盒。现在仓库里有m张正方形纸板和n张长方形纸板,如果做两种纸盒若干个,恰好使库存的纸板用完,则 的值可能是( )
的值可能是( )  A、2013 B、2014 C、2015 D、201610. 如图,8块相同的小长方形地砖拼成一个长方形,其中每一个小长方形的面积为( )
A、2013 B、2014 C、2015 D、201610. 如图,8块相同的小长方形地砖拼成一个长方形,其中每一个小长方形的面积为( ) A、400cm2 B、500cm2 C、600cm2 D、675cm2
A、400cm2 B、500cm2 C、600cm2 D、675cm2二、填空题
-
11. 《九章算术》中记载:“今有牛五、羊二,直金十两;牛二、羊五,直金八两.问:牛、羊各直金几何?”
译文:“假设有5头牛、2只羊,值金10两;2头牛、5只羊,值金8两.问:每头牛、每只羊各值金多少两?”设每头牛值金x两,每只羊值金y两,可列方程组为 .
12. 为了奖励数学社团的同学,张老师恰好用100元在网上购买《数学史话》、《趣味数学》两种书(两种书都购买了若干本),已知《数学史话》每本10元,《趣味数学》每本6元, 则张老师最多购买了《数学史话》.13. 小林、小芳和小亮三人玩飞镖游戏,各投5支飞镖,规定在同一圆环内得分相同,中靶和得分情况如图,则小亮的得分是分. 14. 已知 ,那么 =。15. 一架飞机顺风飞行,每小时飞行500km,逆风飞行,每小时飞行460km,假设飞机本身的速度是xkm/h,风速是ykm/h,依题意列出二元一次方程组 .16. 用白铁皮做罐头盒,每张铁皮可制盒身25个,或制盒底40个,一个盒身可以和两个盒底可制成一个罐头盒.现有36张白铁皮,设用x张制盒身,y张制盒底,恰好配套制成罐头盒,根据题意,可列方程组.
14. 已知 ,那么 =。15. 一架飞机顺风飞行,每小时飞行500km,逆风飞行,每小时飞行460km,假设飞机本身的速度是xkm/h,风速是ykm/h,依题意列出二元一次方程组 .16. 用白铁皮做罐头盒,每张铁皮可制盒身25个,或制盒底40个,一个盒身可以和两个盒底可制成一个罐头盒.现有36张白铁皮,设用x张制盒身,y张制盒底,恰好配套制成罐头盒,根据题意,可列方程组.三、解答题
-
17. 张新是某县城中学的在校住宿生,开学初父母通过估算为他预存了一个学期的伙食费1600元,学校的学生食堂规定一天的伙食标准:早餐每人4元,中餐、晚餐只能各选一份价格如下表中的饭菜.
价格1(单位:元/份)
价格2(单元:元/份)
中餐
5
7
晚餐
5
7
(1)、请问该校每位住宿生一天的伙食费有几种可能的价格?其金额各是多少元?(2)、若张新选择(1)中一天的伙食费的两种价格,并计划用膳110天,且刚好用完预存款,那么他应有哪几种选择价格的方案?每种方案中两种价格各用膳多少天?18. 太仓港区道路绿化工程工地有大量货物需要运输,某车队有载重量为8吨和10吨的卡车共15辆,所有车辆运输一次能运输128吨货物.(1)、求该车队载重量为8吨、10吨的卡车各有多少辆?(2)、随着工程的扩大,车队需要一次运输货物170吨以上,为了完成任务,车队准备增购这两种卡车共5辆(两种车都购买),请写出所有可能的购车方案.19. 一个两位数的十位数字与个位数字之和恰好是9.把它的十位数字与个位数字对调,得到了一个新的两位数,这个新的两位数恰好也比原来的两位数大9.求原来的两位数.20. 某寄宿制学校有大、小两种类型的学生宿舍共50间,大宿舍每间可住8人,小宿舍每间可住6人.该校360名住宿生恰好住满50间宿舍.求大、小宿舍各有多少间?21. 已知小明骑车和步行的速度分别为240米/分,80米/分,小红每次从家步行到学校所需时间相同.请你根据小红和小明的对话内容(如图),求小明从家到学校的路程和小红从家步行到学校所需的时间. 22. 在某超市小明买了1千克甲种糖果和2千克乙种糖果,共付38元;小强买了2千克甲种糖果和0.5千克乙种糖果,共付27元.(1)、求该超市甲、乙两种糖果每千克各需多少元?(2)、某顾客到该超市购买甲、乙两种糖果共20千克混合,欲使总价不超过240元,问该顾客混合的糖果中甲种糖果最少多少千克?23. 某校规划在一块长AD为18m,宽AB为13m的长方形场地ABCD上,设计分别与AD,AB平行的横向通道和纵向通道(通道面积不超过总面积的 ),其余部分铺上草皮.
22. 在某超市小明买了1千克甲种糖果和2千克乙种糖果,共付38元;小强买了2千克甲种糖果和0.5千克乙种糖果,共付27元.(1)、求该超市甲、乙两种糖果每千克各需多少元?(2)、某顾客到该超市购买甲、乙两种糖果共20千克混合,欲使总价不超过240元,问该顾客混合的糖果中甲种糖果最少多少千克?23. 某校规划在一块长AD为18m,宽AB为13m的长方形场地ABCD上,设计分别与AD,AB平行的横向通道和纵向通道(通道面积不超过总面积的 ),其余部分铺上草皮. (1)、如图1,若设计两条通道,一条横向,一条纵向,4块草坪为全等的长方形,每块草坪的两边之比为3:4,并且纵向通道的宽度是横向通道宽度的2倍,问横向通道的宽是多少?(2)、如图2,为设计得更美观,其中草坪①②③④为全等的正方形,草坪⑤⑥为全等的长方形(两边长BN:BM=2:3),通道宽度都相等,问:此时通道的宽度又是多少呢?24. 济南市某玻璃制品销售公司今年1月份调整了职工的月工资分配方案,调整后月工资由基本保障工资和计件奖励工资两部分组成(计件奖励工资=销售每件的奖励金额×销售的件数).下表是甲、乙两位职工今年五月份的工资情况信息:
(1)、如图1,若设计两条通道,一条横向,一条纵向,4块草坪为全等的长方形,每块草坪的两边之比为3:4,并且纵向通道的宽度是横向通道宽度的2倍,问横向通道的宽是多少?(2)、如图2,为设计得更美观,其中草坪①②③④为全等的正方形,草坪⑤⑥为全等的长方形(两边长BN:BM=2:3),通道宽度都相等,问:此时通道的宽度又是多少呢?24. 济南市某玻璃制品销售公司今年1月份调整了职工的月工资分配方案,调整后月工资由基本保障工资和计件奖励工资两部分组成(计件奖励工资=销售每件的奖励金额×销售的件数).下表是甲、乙两位职工今年五月份的工资情况信息:职工
甲
乙
月销售件数(件)
200
180
月工资(元)
1800
1700
(1)、试求工资分配方案调整后职工的月基本保障工资和销售每件产品的奖励金额各多少元?(2)、若职工丙今年六月份的工资不低于2000元,那么丙该月至少应销售多少件产品?25. 今有鸡兔同笼,上有二十六头,下有八十二足,问鸡兔各几何?(1)、根据上面文字求出鸡兔各有多少只?(2)、若设A为鸡兔总共只数,B为鸡兔总共足数,请你运用方程组探索兔数、A、B之间的关系,并将你发现的结论用等式表示出来?