2018-2019学年初中数学北师大版九年级下册1.5-1.6 同步练习
试卷更新日期:2019-01-14 类型:同步测试
一、单选题
-
1. 如图,修建抽水站时,沿着坡度为i=1: 的斜坡铺设水管.若测得水管A处铅垂高度为8 m,则所铺设水管AC的长度为( )
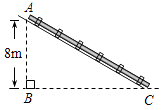 A、8m B、12m C、14m D、16m2. “新中梁山隧道”于2017年11月21日开放通行,原中梁山隧道将封闭升级,扩容改造工程预计2018年3月全部完工,届时将实现双向8车道通行,隧道通行能力将增加一倍,沿线交通拥堵状况将有所缓解.图中线段AB表示该工程的部分隧道.无人勘测机从隧道侧的A点出发时,测得C点正上方的E点的仰角为45°,无人机飞行到E点后,沿着坡度i=1:3的路线EB飞行,飞行到D点正上方的F点时,测得A点的俯角为12°,其中EC=100米,A,B,C,D,E,F在同一平面内,则隧道AD段的长度约为( )米,(参考数据:tan12°≈0.2,cosl2°≈0.98)
A、8m B、12m C、14m D、16m2. “新中梁山隧道”于2017年11月21日开放通行,原中梁山隧道将封闭升级,扩容改造工程预计2018年3月全部完工,届时将实现双向8车道通行,隧道通行能力将增加一倍,沿线交通拥堵状况将有所缓解.图中线段AB表示该工程的部分隧道.无人勘测机从隧道侧的A点出发时,测得C点正上方的E点的仰角为45°,无人机飞行到E点后,沿着坡度i=1:3的路线EB飞行,飞行到D点正上方的F点时,测得A点的俯角为12°,其中EC=100米,A,B,C,D,E,F在同一平面内,则隧道AD段的长度约为( )米,(参考数据:tan12°≈0.2,cosl2°≈0.98) A、200 B、250 C、300 D、5403. 如图,小颖利用一个锐角是30°的三角板测量一棵树的高度,已知她与树之间的水平距离BE为5m,AB为1.5m(即小颖的眼睛距地面的距离),那么这棵树高是( )
A、200 B、250 C、300 D、5403. 如图,小颖利用一个锐角是30°的三角板测量一棵树的高度,已知她与树之间的水平距离BE为5m,AB为1.5m(即小颖的眼睛距地面的距离),那么这棵树高是( ) A、4m B、 m C、(5 + )m D、( + )m4. 如图,某轮船在点O处测得一个小岛上的电视塔A在北偏西60°的方向,船向西航行20海里到达B处,测得电视塔A在船的西北方向,若要轮船离电视塔最近,则还需向西航行( )
A、4m B、 m C、(5 + )m D、( + )m4. 如图,某轮船在点O处测得一个小岛上的电视塔A在北偏西60°的方向,船向西航行20海里到达B处,测得电视塔A在船的西北方向,若要轮船离电视塔最近,则还需向西航行( ) A、 海里 B、 海里 C、 海里 D、 海里5. 如图,电线杆CD的高度为h,两根拉线AC与BC相互垂直,∠CAB=α,则拉线BC的长度为(A、D、B在同一条直线上)( )
A、 海里 B、 海里 C、 海里 D、 海里5. 如图,电线杆CD的高度为h,两根拉线AC与BC相互垂直,∠CAB=α,则拉线BC的长度为(A、D、B在同一条直线上)( )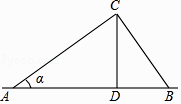 A、 B、 C、 D、h•cosα6.
A、 B、 C、 D、h•cosα6.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米.则小巷的宽度为( )
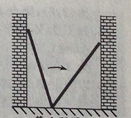 A、0.7米 B、1.5米 C、2.2米 D、2.4米7. 为测量被池塘相隔的两棵树 , 的距离,数学课外兴趣小组的同学们设计了如图所示的测量方案:从树 沿着垂直于 的方向走到 ,再从 沿着垂直于 的方向走到 , 为 上一点。其中 位同学分别测得三组数据:(1) , ;(2) , , ;(3) , , 。其中能根据所测数据求得 , 两树距离的有( )
A、0.7米 B、1.5米 C、2.2米 D、2.4米7. 为测量被池塘相隔的两棵树 , 的距离,数学课外兴趣小组的同学们设计了如图所示的测量方案:从树 沿着垂直于 的方向走到 ,再从 沿着垂直于 的方向走到 , 为 上一点。其中 位同学分别测得三组数据:(1) , ;(2) , , ;(3) , , 。其中能根据所测数据求得 , 两树距离的有( )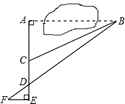 A、0组 B、一组 C、二组 D、三组8. 数学活动课,老师和同学一起去测量校内某处的大树 的高度,如图,老师测得大树前斜坡 的坡度i=1:4,一学生站在离斜坡顶端 的水平距离DF为8m处的D点,测得大树顶端A的仰角为 ,已知 ,BE=1.6m,此学生身高CD=1.6m,则大树高度AB为( )m.
A、0组 B、一组 C、二组 D、三组8. 数学活动课,老师和同学一起去测量校内某处的大树 的高度,如图,老师测得大树前斜坡 的坡度i=1:4,一学生站在离斜坡顶端 的水平距离DF为8m处的D点,测得大树顶端A的仰角为 ,已知 ,BE=1.6m,此学生身高CD=1.6m,则大树高度AB为( )m.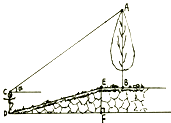 A、7.4 B、7.2 C、7 D、6.89. 小明在某次投篮中刚好把球打到篮板的点D处后进球.已知小明与篮框底的距离BC=5米,眼睛与地面的距离AB= 米,视线AD与水平线的夹角为∠α,已知tanα= , 则点D到地面的距离CD是( )
A、7.4 B、7.2 C、7 D、6.89. 小明在某次投篮中刚好把球打到篮板的点D处后进球.已知小明与篮框底的距离BC=5米,眼睛与地面的距离AB= 米,视线AD与水平线的夹角为∠α,已知tanα= , 则点D到地面的距离CD是( )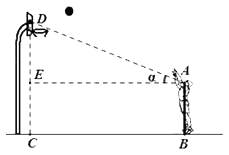 A、2.7米 B、3.0米 C、3.2米 D、3.4米10. 如图,一艘海轮位于灯塔P的南偏东45°方向,距离灯塔30海里的A处,它沿正北方向航行一段时间后,到达位于灯塔P的北偏东30°方向上的B处,这时,B处于灯塔P的距离为( )
A、2.7米 B、3.0米 C、3.2米 D、3.4米10. 如图,一艘海轮位于灯塔P的南偏东45°方向,距离灯塔30海里的A处,它沿正北方向航行一段时间后,到达位于灯塔P的北偏东30°方向上的B处,这时,B处于灯塔P的距离为( ) A、30 海里 B、15 海里 C、30 海里 D、15 海里11. 已知:岛P位于岛Q的正西方,由岛P、Q分别测得船R位于南偏东30°和南偏西45°方向上,则符合条件的示意图是( )A、
A、30 海里 B、15 海里 C、30 海里 D、15 海里11. 已知:岛P位于岛Q的正西方,由岛P、Q分别测得船R位于南偏东30°和南偏西45°方向上,则符合条件的示意图是( )A、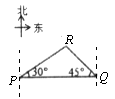 B、
B、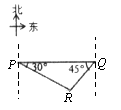 C、
C、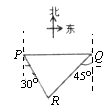 D、
D、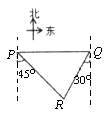 12. 如图,小明要测量河内小岛 B 到河边公路 l 的距离,在 A 点测得∠BAD=30°,在 C 点测得∠BCD=60°,又测得 AC=60米,则小岛 B 到公路 l 的距离为( )
12. 如图,小明要测量河内小岛 B 到河边公路 l 的距离,在 A 点测得∠BAD=30°,在 C 点测得∠BCD=60°,又测得 AC=60米,则小岛 B 到公路 l 的距离为( ) A、30 米 B、30 米 C、40 米 D、(30+ )米13. 如图,王华晚上由路灯A下的B处走到C处时,测得影子CD的长为1米,继续往前走3米到达E处时,测得影子EF的长为2米,已知王华的身高是1.5米,那么路灯A的高度AB等于( )
A、30 米 B、30 米 C、40 米 D、(30+ )米13. 如图,王华晚上由路灯A下的B处走到C处时,测得影子CD的长为1米,继续往前走3米到达E处时,测得影子EF的长为2米,已知王华的身高是1.5米,那么路灯A的高度AB等于( ) A、4.5米 B、6米 C、7.2米 D、8米14. 重庆一中研究性学习小组准备利用所学的三角函数的知识取测量南山大金鹰的高度.他们在B处测得山顶C的仰角是45°,从B沿坡度为1: 的斜度前进38米到达大金鹰上的一个观景点D,再次测得山顶C的仰角为60°,则大金鹰的高度AC为( )米(结果精确到1米.参考数据 ≈1.41, ≈1.73)
A、4.5米 B、6米 C、7.2米 D、8米14. 重庆一中研究性学习小组准备利用所学的三角函数的知识取测量南山大金鹰的高度.他们在B处测得山顶C的仰角是45°,从B沿坡度为1: 的斜度前进38米到达大金鹰上的一个观景点D,再次测得山顶C的仰角为60°,则大金鹰的高度AC为( )米(结果精确到1米.参考数据 ≈1.41, ≈1.73) A、45 B、48 C、52 D、5415. 一组正方形按如图所示的方式放置,其中顶点B1在y轴上,顶点C1 , E1 , E2 , C2 , E3 , E4 , C3…在x轴上,已知正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3…则正方形A2018B2018C2018D2018的边长是( )
A、45 B、48 C、52 D、5415. 一组正方形按如图所示的方式放置,其中顶点B1在y轴上,顶点C1 , E1 , E2 , C2 , E3 , E4 , C3…在x轴上,已知正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3…则正方形A2018B2018C2018D2018的边长是( )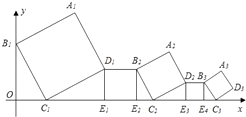 A、( )2017 B、( )2016 C、( )2017 D、( )2016
A、( )2017 B、( )2016 C、( )2017 D、( )2016二、填空题
-
16. 如图,铁路的路基是等腰梯形ABCD,斜坡AD、BC的坡度i=1:1.5,路基AE高为3米,现由单线改为复线,路基需加宽4米,(即AH=4米),加宽后也成等腰梯形,且GH、BF斜坡的坡度i'=1:2,若路长为10000米,则加宽的土石方量共是立方米.
 17. 如图,某办公大楼正前方有一根高度是15米的旗杆ED,从办公楼顶端A测得旗杆顶端E的俯角α是45°,旗杆底端D到大楼前梯坎底边的距离DC是20米,梯坎坡长BC是12米,梯坎坡度i=1∶ ,求大楼AB的高度是?(结果保留根号)
17. 如图,某办公大楼正前方有一根高度是15米的旗杆ED,从办公楼顶端A测得旗杆顶端E的俯角α是45°,旗杆底端D到大楼前梯坎底边的距离DC是20米,梯坎坡长BC是12米,梯坎坡度i=1∶ ,求大楼AB的高度是?(结果保留根号)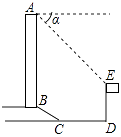 18. 如图,是矗立在高速公路水平地面上的交通警示牌,经测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,则警示牌的高CD为米(结果保留根号).
18. 如图,是矗立在高速公路水平地面上的交通警示牌,经测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,则警示牌的高CD为米(结果保留根号).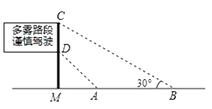 19. 为解决停车难的问题,在如图所示的一段长56米的路段开辟停车位,每个车位是长5米,宽2.2米的矩形,矩形的边与路的边缘成45°角,那么这个路段最多可以划出个这样的停车位.
19. 为解决停车难的问题,在如图所示的一段长56米的路段开辟停车位,每个车位是长5米,宽2.2米的矩形,矩形的边与路的边缘成45°角,那么这个路段最多可以划出个这样的停车位. 20. 如图,小阳发现电线杆AB的影子落在土坡的坡面CD和地面BC上,量得CD=8米,BC=20米,CD与地面成30°角,且此时测得1米的竹竿影长为2米,则电线杆的高度为。
20. 如图,小阳发现电线杆AB的影子落在土坡的坡面CD和地面BC上,量得CD=8米,BC=20米,CD与地面成30°角,且此时测得1米的竹竿影长为2米,则电线杆的高度为。 21. 如图,从与旗杆AB相距27m的点C处,用测角仪CD测得旗杆顶端A的仰角为30°,已知测角仪CD的高为1.5米,则旗杆AB的高约为m(精确到0.1m,参考数据 ≈1.73)
21. 如图,从与旗杆AB相距27m的点C处,用测角仪CD测得旗杆顶端A的仰角为30°,已知测角仪CD的高为1.5米,则旗杆AB的高约为m(精确到0.1m,参考数据 ≈1.73)
三、解答题
-
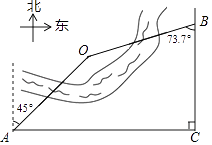
22. 某区域平面示意图如图,点O在河的一侧,AC和BC表示两条互相垂直的公路.甲勘测员在A处测得点O位于北偏东45°,乙勘测员在B处测得点O位于南偏西73.7°,测得AC=840m,BC=500m.请求出点O到BC的距离.
参考数据:sin73.7°≈ ,cos73.7°≈ ,tan73.7°≈
 23. 2017年9月8日﹣10日,第六届翼装飞行世界锦标赛在我市天门山风景区隆重举行,来自全球11个国家的16名选手参加了激烈的角逐.如图,某选手从离水平地面1000米高的A点出发(AB=1000米),沿俯角为30°的方向直线飞行1400米到达D点,然后打开降落伞沿俯角为60°的方向降落到地面上的C点,求该选手飞行的水平距离BC.
23. 2017年9月8日﹣10日,第六届翼装飞行世界锦标赛在我市天门山风景区隆重举行,来自全球11个国家的16名选手参加了激烈的角逐.如图,某选手从离水平地面1000米高的A点出发(AB=1000米),沿俯角为30°的方向直线飞行1400米到达D点,然后打开降落伞沿俯角为60°的方向降落到地面上的C点,求该选手飞行的水平距离BC. 24.
24.在学习完“利用三角函数测高”这节内容之后,某兴趣小组开展了测量学校旗杆高度的实践活动,如图,在测点A处安置测倾器,量出高度AB=1.5m,测得旗杆顶端D的仰角∠DBE=32°,量出测点A到旗杆底部C的水平距离AC=20m,根据测量数据,求旗杆CD的高度.(参考数据:sin32°≈0.53,cos32°≈0.85,tan32°≈0.62)
 25. 如图,贵阳市某中学数学活动小组在学习了“利用三角函数测高”后.选定测量小河对岸一幢建筑物BC的高度.他们先在斜坡上的D处,测得建筑物顶的仰角为30°.且D离地面的高度DE=5m.坡底EA=10m,然后在A处测得建筑物顶B的仰角是50°,点E,A,C在同一水平线上,求建筑物BC的高.(结果保留整数)
25. 如图,贵阳市某中学数学活动小组在学习了“利用三角函数测高”后.选定测量小河对岸一幢建筑物BC的高度.他们先在斜坡上的D处,测得建筑物顶的仰角为30°.且D离地面的高度DE=5m.坡底EA=10m,然后在A处测得建筑物顶B的仰角是50°,点E,A,C在同一水平线上,求建筑物BC的高.(结果保留整数)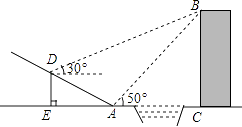 26. 近年来,共享单车服务的推出 如图 ,极大的方便了城市公民绿色出行,图2是某品牌某型号单车的车架新投放时的示意图 车轮半径约为 ,其中 直线l, , .
26. 近年来,共享单车服务的推出 如图 ,极大的方便了城市公民绿色出行,图2是某品牌某型号单车的车架新投放时的示意图 车轮半径约为 ,其中 直线l, , .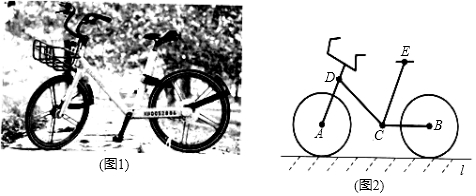
参考数据: , ,
(1)、求单车车座E到地面的高度; 结果精确到
(2)、根据经验,当车座E到CB的距离调整至等于人体胯高 腿长 的 时,坐骑比较舒适 小明的胯高为70cm,现将车座E调整至座椅舒适高度位置 ,求 的长 结果精确到
27. 某商场要修建一个地下停车场,停车场的入口设计示意图如图所示,其中斜坡的倾斜角为18°,一楼到地下停车场地面的距离CD=2.8米,一楼到地平线的距离BC=1米.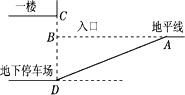 (1)、为保证斜坡的倾斜角为18°,应在地面上距点B多远的A处开始斜坡的施工?(结果精确到0.1米)(2)、如果给该商场送货的货车高度为2.5米,那么按这样的设计能否保证货车顺利进入地下停车场?请说明理由.(参考数据:sin 18°≈0.31,cos 18°≈0.95,tan 18°≈0.32)
(1)、为保证斜坡的倾斜角为18°,应在地面上距点B多远的A处开始斜坡的施工?(结果精确到0.1米)(2)、如果给该商场送货的货车高度为2.5米,那么按这样的设计能否保证货车顺利进入地下停车场?请说明理由.(参考数据:sin 18°≈0.31,cos 18°≈0.95,tan 18°≈0.32)
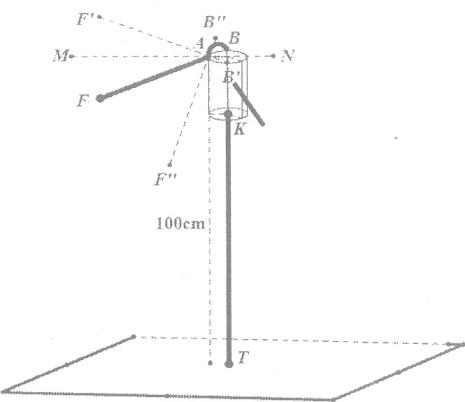
28. 如图,是井用手摇抽水机的示意图,支点A的左端是一手柄,右端是一弯钩,点F,A,B始终在同一直线上,支点A距离地面100cm,与手柄端点F之间的距离AF=50cm,与弯钩端点B之间的距离AB=10cm.KT为进水管.
 (1)、在一次取水过程中,将手柄AF绕支点A旋转到AF',且与水平线MN的夹角为20°,且此时点B',K,T在一条线上,求点F'离地面的高度.(2)、当不取水时,将手柄绕支点A逆时针旋转90°至点F''位置,求端点F''与进水管KT之间的距离.(忽略进水管的粗细)(参考数据: ≈0.34, ≈0.94, ≈0.36)29. 如图,湖中的小岛上有一标志性建筑物,其底部为A,某人在岸边的B处测得A在B的北偏东30°的方向上,然后沿岸边直行4公里到达C处,再次测得A在C的北偏西45°的方向上(其中A,B,C在同一平面上).如果某人要从BC路上的某点D去A点,要求AD是距离最短的路线.(精确到0.1公里, , ).
(1)、在一次取水过程中,将手柄AF绕支点A旋转到AF',且与水平线MN的夹角为20°,且此时点B',K,T在一条线上,求点F'离地面的高度.(2)、当不取水时,将手柄绕支点A逆时针旋转90°至点F''位置,求端点F''与进水管KT之间的距离.(忽略进水管的粗细)(参考数据: ≈0.34, ≈0.94, ≈0.36)29. 如图,湖中的小岛上有一标志性建筑物,其底部为A,某人在岸边的B处测得A在B的北偏东30°的方向上,然后沿岸边直行4公里到达C处,再次测得A在C的北偏西45°的方向上(其中A,B,C在同一平面上).如果某人要从BC路上的某点D去A点,要求AD是距离最短的路线.(精确到0.1公里, , ). (1)、在图中作出点D,并求最短距离;(2)、求BD的长.
(1)、在图中作出点D,并求最短距离;(2)、求BD的长.