2018-2019学年初中数学北师大版九年级下册1.4 解直角三角形 同步练习
试卷更新日期:2019-01-14 类型:同步测试
一、单选题
-
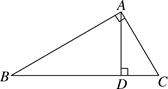
1. 如图,Rt△ABC中,∠BAC=90°,AD⊥BC于D,设∠ABC=α,则下列结论错误的是( )
 A、BC=
A、BC=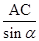 B、CD=AD·tanα
C、AC=AD·cosα
D、BD=AB·cosα
2. 某市为了美化环境,计划在如图所示的三角形空地上种植草皮,已知这种草皮每平方米售价为a元,则购买这种草皮至少需要( )
B、CD=AD·tanα
C、AC=AD·cosα
D、BD=AB·cosα
2. 某市为了美化环境,计划在如图所示的三角形空地上种植草皮,已知这种草皮每平方米售价为a元,则购买这种草皮至少需要( ) A、450a元 B、225a元 C、150a元 D、300a元3. 在Rt△ABC中,∠C=90°,若sin A= ,则∠B的度数是( )A、30° B、45° C、60° D、90°4. 如图,△ABC中,∠C=90°,AC=3,∠B=30°,P是BC边上的动点,则AP长不可能是( )
A、450a元 B、225a元 C、150a元 D、300a元3. 在Rt△ABC中,∠C=90°,若sin A= ,则∠B的度数是( )A、30° B、45° C、60° D、90°4. 如图,△ABC中,∠C=90°,AC=3,∠B=30°,P是BC边上的动点,则AP长不可能是( )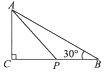 A、3.5 B、4.2 C、5.8 D、75. 已知在△ABC中,AB=14,BC=13,tanB= ,则sinA的值为( )
A、3.5 B、4.2 C、5.8 D、75. 已知在△ABC中,AB=14,BC=13,tanB= ,则sinA的值为( )
A、 B、 C、 D、6. 如何求tan75°的值?按下列方法作图可解决问题,如图,在Rt△ABC中,AC=k,∠ACB=90°,∠ABC=30°,延长CB至点M,在射线BM上截取线段BD,使BD=AB,连接AD,依据此图可求得tan75°的值为( )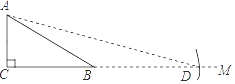 A、2 B、2+ C、1+ D、7. 设a、b、c分别为△ABC中∠A,∠B和∠C的对边,则△ABC的面积为( )A、 B、 C、 D、8. 如图,在等腰Rt△ABC中,∠C=90°,AC=BC=6,D是AC上一点,若tan∠DBA= ,则AD的长为( )
A、2 B、2+ C、1+ D、7. 设a、b、c分别为△ABC中∠A,∠B和∠C的对边,则△ABC的面积为( )A、 B、 C、 D、8. 如图,在等腰Rt△ABC中,∠C=90°,AC=BC=6,D是AC上一点,若tan∠DBA= ,则AD的长为( ) A、2 B、 C、 D、19. 如图,在矩形ABCD中,AB=3,AD=5,点E在DC上,将矩形ABCD沿AE折叠,点D恰好落在BC边上的点F处,那么cos∠EFC的值是( )
A、2 B、 C、 D、19. 如图,在矩形ABCD中,AB=3,AD=5,点E在DC上,将矩形ABCD沿AE折叠,点D恰好落在BC边上的点F处,那么cos∠EFC的值是( )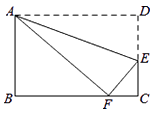 A、 B、 C、 D、10. 如图,在△ABC中,∠B=90°,tan∠C= ,AB=6cm.动点P从点A开始沿边AB向点B以1cm/s的速度移动,动点Q从点B开始沿边BC向点C以2cm/s的速度移动.若P,Q两点分别从A,B两点同时出发,在运动过程中,△PBQ的最大面积是( )
A、 B、 C、 D、10. 如图,在△ABC中,∠B=90°,tan∠C= ,AB=6cm.动点P从点A开始沿边AB向点B以1cm/s的速度移动,动点Q从点B开始沿边BC向点C以2cm/s的速度移动.若P,Q两点分别从A,B两点同时出发,在运动过程中,△PBQ的最大面积是( )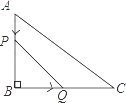 A、18cm2 B、12cm2 C、9cm2 D、3cm2
A、18cm2 B、12cm2 C、9cm2 D、3cm2二、填空题
-
11. Rt△ABC中,∠A = 3∠C = 90°,AB = 3,点Q在边AB上且BQ = ,过Q作QF∥BC交AC于点F,点P在线段QF上,过P作PD∥AC交AB于点D,PE∥AB交BC于点E,当P到△ABC的三边的距离之和为3时,PD + PE + PF =.
12. 如图,Rt△ABC中,∠C=90°,∠ABC=30°,AC=2,△ABC绕点C顺时针旋转得△A1B1C,当A1落在AB边上时,连接B1B,取BB1的中点D,连接A1D,则A1D的长度是 . 13. 如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为3:4,∠OCD=90°,∠AOB=60°,若点B的坐标是(6,0),则点C的坐标是 .
13. 如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为3:4,∠OCD=90°,∠AOB=60°,若点B的坐标是(6,0),则点C的坐标是 .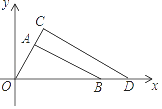 14. 如图,在▱ABCD中,AD=7,AB=2 ,∠B=60°.E是边BC上任意一点,沿AE剪开,将△ABE沿BC方向平移到△DCF的位置,得到四边形AEFD,则四边形AEFD周长的最小值为 .
14. 如图,在▱ABCD中,AD=7,AB=2 ,∠B=60°.E是边BC上任意一点,沿AE剪开,将△ABE沿BC方向平移到△DCF的位置,得到四边形AEFD,则四边形AEFD周长的最小值为 .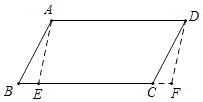 15. 如图,在边长为1的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点O,则tan∠AOD=.
15. 如图,在边长为1的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点O,则tan∠AOD=. 16. 如图,等边三角形ABC的边长为2,D,E分别是边AB,AC上的点,沿DE所在的直线折叠∠A,使点A的对应点P始终落在边BC上,若△BDP是直角三角形,则AD的长为 .
16. 如图,等边三角形ABC的边长为2,D,E分别是边AB,AC上的点,沿DE所在的直线折叠∠A,使点A的对应点P始终落在边BC上,若△BDP是直角三角形,则AD的长为 .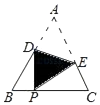
三、解答题
-
17. 如图,已知∠MON=25°,矩形ABCD的边BC在OM上,对角线AC⊥ON.
 (1)、求∠ACD度数;(2)、当AC=5时,求AD的长.(参考数据:sin25°=0.42;cos25°=0.91;tan25°=0.47,结果精确到0.1)18. 已知:如图,AD∥BC,AB=CD,对角线CA平分∠BCD,AD=5,tanB= ,求BC的长.
(1)、求∠ACD度数;(2)、当AC=5时,求AD的长.(参考数据:sin25°=0.42;cos25°=0.91;tan25°=0.47,结果精确到0.1)18. 已知:如图,AD∥BC,AB=CD,对角线CA平分∠BCD,AD=5,tanB= ,求BC的长.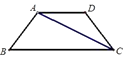 19. 已知:如图,在Rt△ABC中,∠ACB=90°,BC= ,cot∠ABC= ,点D是AC的中点.
19. 已知:如图,在Rt△ABC中,∠ACB=90°,BC= ,cot∠ABC= ,点D是AC的中点. (1)、求线段BD的长;(2)、点E在边AB上,且CE=CB,求△ACE的面积.20. “C919”大型客机首飞成功,激发了同学们对航空科技的兴趣,如图是某校航模兴趣小组获得的一张数据不完整的航模飞机机翼图纸,图中AB∥CD,AM∥BN∥ED,AE⊥DE,请根据图中数据,求出线段BE和CD的长.(sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,结果保留小数点后一位)
(1)、求线段BD的长;(2)、点E在边AB上,且CE=CB,求△ACE的面积.20. “C919”大型客机首飞成功,激发了同学们对航空科技的兴趣,如图是某校航模兴趣小组获得的一张数据不完整的航模飞机机翼图纸,图中AB∥CD,AM∥BN∥ED,AE⊥DE,请根据图中数据,求出线段BE和CD的长.(sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,结果保留小数点后一位)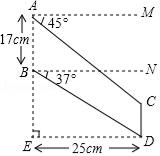 21. 经过江汉平原的沪蓉(上海﹣成都)高速铁路即将动工.工程需要测量汉江某一段的宽度.如图①,一测量员在江岸边的A处测得对岸岸边的一根标杆B在它的正北方向,测量员从A点开始沿岸边向正东方向前进100米到达点C处,测得∠ACB=68°.
21. 经过江汉平原的沪蓉(上海﹣成都)高速铁路即将动工.工程需要测量汉江某一段的宽度.如图①,一测量员在江岸边的A处测得对岸岸边的一根标杆B在它的正北方向,测量员从A点开始沿岸边向正东方向前进100米到达点C处,测得∠ACB=68°. (1)、求所测之处江的宽度(sin68°≈0.93,cos68°≈0.37,tan68°≈2.48.);(2)、除(1)的测量方案外,请你再设计一种测量江宽的方案,并在图②中画出图形.22. 在 中, , , ,过点 作直线 ,将 绕点 顺时针得到 (点 , 的对应点分别为 , )射线 , 分别交直线 于点 , .
(1)、求所测之处江的宽度(sin68°≈0.93,cos68°≈0.37,tan68°≈2.48.);(2)、除(1)的测量方案外,请你再设计一种测量江宽的方案,并在图②中画出图形.22. 在 中, , , ,过点 作直线 ,将 绕点 顺时针得到 (点 , 的对应点分别为 , )射线 , 分别交直线 于点 , .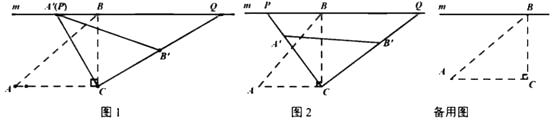 (1)、如图1,当 与 重合时,求 的度数;(2)、如图2,设 与 的交点为 ,当 为 的中点时,求线段 的长;
(1)、如图1,当 与 重合时,求 的度数;(2)、如图2,设 与 的交点为 ,当 为 的中点时,求线段 的长;
(3)、在旋转过程时,当点 分别在 , 的延长线上时,试探究四边形 的面积是否存在最小值.若存在,求出四边形 的最小面积;若不存在,请说明理由.