北京市海淀区2018-2019学年九年级上学期数学期中考试试卷
试卷更新日期:2019-01-14 类型:期中考试
一、选择题
-
1. 抛物线y=x2+1的对称轴是( )A、直线 B、直线 C、直线 D、直线 y=12. 点P(2,-1)关于原点对称的点P′的坐标是( )A、
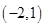 B、
B、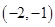 C、
C、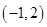 D、
D、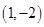 3. 下列App图标中,既不是中心对称图形也不是轴对称图形的是( )A、
3. 下列App图标中,既不是中心对称图形也不是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 4. 用配方法解方程x2-2x-4=0,配方正确的是( )A、
4. 用配方法解方程x2-2x-4=0,配方正确的是( )A、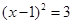 B、
B、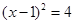 C、
C、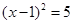 D、
D、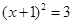 5. 如图,以O为圆心的两个同心圆中,大圆的弦AB是小圆的切线,点P为切点.若大圆半径为2,小圆半径为1,则AB的长为( )
5. 如图,以O为圆心的两个同心圆中,大圆的弦AB是小圆的切线,点P为切点.若大圆半径为2,小圆半径为1,则AB的长为( )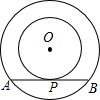 A、 B、 C、
A、 B、 C、
D、26. 将抛物线y=(x+1)2-2向上平移a个单位后得到的抛物线恰好与x轴有一个交点,则a的值为( )A、 B、1 C、 D、27. 如图是几种汽车轮毂的图案,图案绕中心旋转90°后能与原来的图案重合的是( )A、 B、
B、 C、
C、 D、
D、 8. 已知一个二次函数图象经过P1(-3,y1),P2(-1,y2),P3(1,y3),P4(3,y4)四点,若y3<y2<y4 , 则y1 , y2 , y3 , y4的最值情况是( )A、 最小, 最大 B、 最小,
8. 已知一个二次函数图象经过P1(-3,y1),P2(-1,y2),P3(1,y3),P4(3,y4)四点,若y3<y2<y4 , 则y1 , y2 , y3 , y4的最值情况是( )A、 最小, 最大 B、 最小,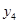 最大
C、 最小,
最大
C、 最小,  最大
D、无法确定
最大
D、无法确定
二、填空题
-
9. 写出一个以0和2为根的一元二次方程: .10. 若二次函数y=ax2+bx+c的图象如图所示,则ac0(填“>”或“=”或“<”).
 11. 若关于x的方程x2-4x+k-1=0有两个不相等的实数根,则k的取值范围是 .12. 如图,四边形ABCD内接于⊙O,E为直径CD延长线上一点,且AB∥CD,若∠C=70°,则∠ADE的大小为 .
11. 若关于x的方程x2-4x+k-1=0有两个不相等的实数根,则k的取值范围是 .12. 如图,四边形ABCD内接于⊙O,E为直径CD延长线上一点,且AB∥CD,若∠C=70°,则∠ADE的大小为 . 13. 已知O为△ABC的外接圆圆心,若O在△ABC外,则△ABC是(填“锐角三角形”或“直角三角形”或“钝角三角形”).14. 在十三届全国人大一次会议记者会上,中国科技部部长表示,2017年我国新能源汽车保有量已居于世界前列.2015年和2017年我国新能源汽车保有量如图所示.设我国2015至2017年新能源汽车保有量年平均增长率为x,依题意,可列方程为 .
13. 已知O为△ABC的外接圆圆心,若O在△ABC外,则△ABC是(填“锐角三角形”或“直角三角形”或“钝角三角形”).14. 在十三届全国人大一次会议记者会上,中国科技部部长表示,2017年我国新能源汽车保有量已居于世界前列.2015年和2017年我国新能源汽车保有量如图所示.设我国2015至2017年新能源汽车保有量年平均增长率为x,依题意,可列方程为 .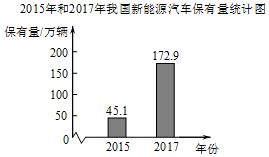 15. 如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+c与x轴交于(1,0),(3,0)两点,请写出一个满足y<0的x的值 .
15. 如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+c与x轴交于(1,0),(3,0)两点,请写出一个满足y<0的x的值 .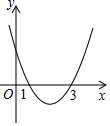 16. 如图,⊙O的动弦AB,CD相交于点E,且AB=CD,∠BED=α(0°<α<90°).在①∠BOD=α,②∠OAB=90°-α,③∠ABC= α中,一定成立的是(填序号).
16. 如图,⊙O的动弦AB,CD相交于点E,且AB=CD,∠BED=α(0°<α<90°).在①∠BOD=α,②∠OAB=90°-α,③∠ABC= α中,一定成立的是(填序号).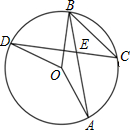
三、计算题
-
17. 解方程:x(x+2)=3x+6.
四、解答题
-
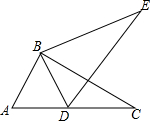
18. 如图,将△ABC绕点B旋转得到△DBE,且A,D,C三点在同一条直线上.求证:DB平分∠ADE.
 19. 下面是小董设计的“作已知圆的内接正三角形”的尺规作图过程.
19. 下面是小董设计的“作已知圆的内接正三角形”的尺规作图过程.已知:⊙O.
求作:⊙O的内接正三角形.
作法:如图,
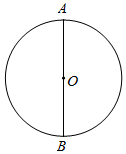
作直径AB;
②以B为圆心,OB为半径作弧,与⊙O交于C,D两点;
③连接AC,AD,CD.
所以△ACD就是所求的三角形.
根据小董设计的尺规作图过程,
(1)、使用直尺和圆规,补全图形;(保留作图痕迹)(2)、完成下面的证明:证明:在⊙O中,连接OC,OD,BC,BD,
∵OC=OB=BC,
∴△OBC为等边三角形()(填推理的依据).
∴∠BOC=60°.
∴∠AOC=180°-∠BOC=120°.
同理∠AOD=120°,
∴∠COD=∠AOC=∠AOD=120°.
∴AC=CD=AD()(填推理的依据).
∴△ACD是等边三角形.
20. 已知-1是方程x2+ax-b=0的一个根,求a2-b2+2b的值.21. 生活中看似平常的隧道设计也很精巧.如图是一张盾构隧道断面结构图,隧道内部为以O为圆心AB为直径的圆.隧道内部共分为三层,上层为排烟道,中间为行车隧道,下层为服务层.点A到顶棚的距离为0.8a,顶棚到路面的距离是3.2a,点B到路面的距离为2a.请你求出路面的宽度l.(用含a的式子表示)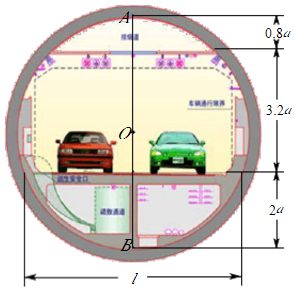 22. 如图,在平面直角坐标系xOy中,抛物线y=x2+ax+b经过点A(-2,0),B(-1,3).
22. 如图,在平面直角坐标系xOy中,抛物线y=x2+ax+b经过点A(-2,0),B(-1,3).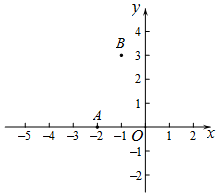 (1)、求抛物线的解析式;(2)、设抛物线的顶点为C,直接写出点C的坐标和∠BOC的度数.23. 如图,用长为6m的铝合金条制成“日”字形窗框,若窗框的宽为x m,窗户的透光面积为y m2(铝合金条的宽度不计).
(1)、求抛物线的解析式;(2)、设抛物线的顶点为C,直接写出点C的坐标和∠BOC的度数.23. 如图,用长为6m的铝合金条制成“日”字形窗框,若窗框的宽为x m,窗户的透光面积为y m2(铝合金条的宽度不计). (1)、求出y与x的函数关系式;(2)、如何安排窗框的长和宽,才能使得窗户的透光面积最大?并求出此时的最大面积.24. 如图,在△ABC中,AB=AC,以AB为直径作⊙O交BC于点D,过点D作AC的垂线交AC于点E,交AB的延长线于点F.
(1)、求出y与x的函数关系式;(2)、如何安排窗框的长和宽,才能使得窗户的透光面积最大?并求出此时的最大面积.24. 如图,在△ABC中,AB=AC,以AB为直径作⊙O交BC于点D,过点D作AC的垂线交AC于点E,交AB的延长线于点F.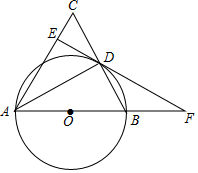 (1)、求证:DE与⊙O相切;(2)、若CD=BF,AE=3,求DF的长.25. 有这样一个问题:探究函数y= 的图象与性质.
(1)、求证:DE与⊙O相切;(2)、若CD=BF,AE=3,求DF的长.25. 有这样一个问题:探究函数y= 的图象与性质.小东根据学习函数的经验,对函数y= 的图象与性质进行了探究.
下面是小东的探究过程,请补充完成:
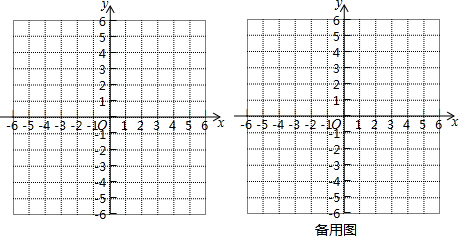 (1)、化简函数解析式,当x≥3时,y= , 当x<3时y=;(2)、根据(1)中的结果,请在所给坐标系中画出函数y= 的图象;(3)、结合画出的函数图象,解决问题:若关于x的方程ax+1= 只有一个实数根,直接写出实数a的取值范围: .26. 在平面直角坐标系xOy中,抛物线y=ax2-2x(a≠0)与x轴交于点A,B(点A在点B的左侧).(1)、当a=-1时,求A,B两点的坐标;(2)、过点P(3,0)作垂直于x轴的直线l,交抛物线于点C.
(1)、化简函数解析式,当x≥3时,y= , 当x<3时y=;(2)、根据(1)中的结果,请在所给坐标系中画出函数y= 的图象;(3)、结合画出的函数图象,解决问题:若关于x的方程ax+1= 只有一个实数根,直接写出实数a的取值范围: .26. 在平面直角坐标系xOy中,抛物线y=ax2-2x(a≠0)与x轴交于点A,B(点A在点B的左侧).(1)、当a=-1时,求A,B两点的坐标;(2)、过点P(3,0)作垂直于x轴的直线l,交抛物线于点C.①当a=2时,求PB+PC的值;
②若点B在直线l左侧,且PB+PC≥14,结合函数的图象,直接写出a的取值范围.
27. 已知∠MON=α,P为射线OM上的点,OP=1. (1)、如图1,α=60°,A,B均为射线ON上的点,OA=1,OB>OA,△PBC为等边三角形,且O,C两点位于直线PB的异侧,连接AC.
(1)、如图1,α=60°,A,B均为射线ON上的点,OA=1,OB>OA,△PBC为等边三角形,且O,C两点位于直线PB的异侧,连接AC.①依题意将图1补全;
②判断直线AC与OM的位置关系并加以证明;
(2)、若α=45°,Q为射线ON上一动点(Q与O不重合),以PQ为斜边作等腰直角△PQR,使O,R两点位于直线PQ的异侧,连接OR.根据(1)的解答经验,直接写出△POR的面积.28. 在平面直角坐标系xOy中,点A是x轴外的一点,若平面内的点B满足:线段AB的长度与点A到x轴的距离相等,则称点B是点A的“等距点”.(1)、若点A的坐标为(0,2),点P1(2,2),P2(1,-4),P3(- ,1)中,点A的“等距点”是;(2)、若点M(1,2)和点N(1,8)是点A的两个“等距点”,求点A的坐标;(3)、记函数y= x(x>0)的图象为L,⊙T的半径为2,圆心坐标为T(0,t).若在L上存在点M,⊙T上存在点N,满足点N是点M的“等距点”,直接写出t的取值范围.
-