北京市房山区2018-2019学年九年级上学期数学期中考试试卷
试卷更新日期:2019-01-14 类型:期中考试
一、选择题
-
1. 若3x=2y(xy≠0),则下列比例式成立的是( )A、
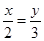 B、
B、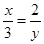 C、
C、 D、
D、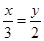 2. 如果两个相似多边形的面积比为4:9,那么它们的周长比为( )A、4:9 B、2:3 C、
2. 如果两个相似多边形的面积比为4:9,那么它们的周长比为( )A、4:9 B、2:3 C、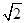 :
D、16:81
3. 已知函数y=(m-3) 是二次函数,则m的值为( )A、 B、
:
D、16:81
3. 已知函数y=(m-3) 是二次函数,则m的值为( )A、 B、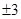 C、3
D、
4. 如图,在△ABC中,点D,E分别在AB,AC上,且DE∥BC,AD=1,BD=2,那么 的值为( )
C、3
D、
4. 如图,在△ABC中,点D,E分别在AB,AC上,且DE∥BC,AD=1,BD=2,那么 的值为( ) A、1:2 B、1:3 C、1:4 D、2:35. 已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.则用电阻R表示电流I的函数表达式为( )
A、1:2 B、1:3 C、1:4 D、2:35. 已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.则用电阻R表示电流I的函数表达式为( ) A、
A、 B、
B、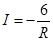 C、
C、
D、 6. 反比例函数y= 的图象经过点(-1,y1),(2,y2),则下列关系正确的是( )A、
6. 反比例函数y= 的图象经过点(-1,y1),(2,y2),则下列关系正确的是( )A、 B、
B、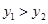 C、
C、 D、不能确定
7. 已知:二次函数y=ax2+bx+c的图象如图所示,下列说法中正确的是( )
D、不能确定
7. 已知:二次函数y=ax2+bx+c的图象如图所示,下列说法中正确的是( ) A、
A、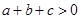 B、
B、 C、
C、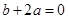
D、 当 ,
, 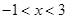 8. 跳台滑雪是冬季奥运会比赛项目之一,运动员起跳后的飞行路线可以看作是抛物线的一部分,运动员起跳后的竖直高度y(单位:m)与水平距离x(单位:m)近似满足函数关系y=ax2+bx+c(a≠0).如图记录了某运动员起跳后的x与y的三组数据,根据上述函数模型和数据,可推断出该运动员起跳后飞行到最高点时,水平距离为( )
8. 跳台滑雪是冬季奥运会比赛项目之一,运动员起跳后的飞行路线可以看作是抛物线的一部分,运动员起跳后的竖直高度y(单位:m)与水平距离x(单位:m)近似满足函数关系y=ax2+bx+c(a≠0).如图记录了某运动员起跳后的x与y的三组数据,根据上述函数模型和数据,可推断出该运动员起跳后飞行到最高点时,水平距离为( ) A、10m B、15m C、20m D、
A、10m B、15m C、20m D、
二、填空题
-
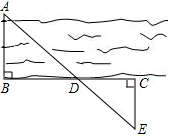
9. 请写出一个开口向上,且与y轴交于(0,-1)的二次函数的解析式 .10. 已知 ,则 = .11. 把抛物线y=x2+1向右平移3个单位,再向下平移2个单位,得到抛物线为 .12. 若x=1是方程2ax2+bx=3的根,当x=2时,函数y=ax2+bx的函数值为 .13. 为了估算河的宽度,我们可以在河对岸的岸边选定一个目标记为点A,再在河的这一边选点B和点C,使得AB⊥BC,然后再在河岸上选点E,使得EC⊥BC,设BC与AE交于点D,如图所示,测得BD=120米,DC=60米,EC=50米,那么这条河的大致宽度是 .
 14. 如图,C1是反比例函数y= 在第一象限内的图象,且过点A(2,1),C2与C1关于x轴对称,那么图象C2对应的函数的表达式为(x>0).
14. 如图,C1是反比例函数y= 在第一象限内的图象,且过点A(2,1),C2与C1关于x轴对称,那么图象C2对应的函数的表达式为(x>0). 15. 如图,小明在A时测得某树的影长为2m,B时又测得该树的影长为8m,若两次日照的光线互相垂直,则树的高度为m.
15. 如图,小明在A时测得某树的影长为2m,B时又测得该树的影长为8m,若两次日照的光线互相垂直,则树的高度为m. 16. 如图,在直角坐标系中,有两个点A(4,0)、B(0,2),如果点C在x轴上(点C与点A不重合),当点C坐标为时,使得由B、O、C三点组成的三角形和△AOB相似.
16. 如图,在直角坐标系中,有两个点A(4,0)、B(0,2),如果点C在x轴上(点C与点A不重合),当点C坐标为时,使得由B、O、C三点组成的三角形和△AOB相似.
三、计算题
-
17. 已知:CD为一幢3米高的温室,其南面窗户的底框G距地面1米,CD在地面上留下的最大影长CF为2米,现欲在距C点7米的正南方A点处建一幢12米高的楼房AB(设A,C,F在同一水平线上).
 (1)、按比例较精确地作出高楼AB及它的最大影长AE;(2)、问若大楼AB建成后是否影响温室CD的采光,试说明理由.
(1)、按比例较精确地作出高楼AB及它的最大影长AE;(2)、问若大楼AB建成后是否影响温室CD的采光,试说明理由.四、解答题
-
18. 已知二次函数y=x2-2x-3.
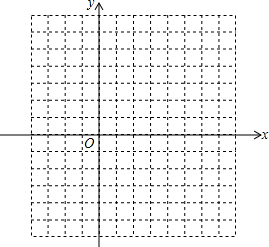 (1)、将y=x2-2x-3化成y=a(x-h)2+k的形式;(2)、与y轴的交点坐标是 , 与x轴的交点坐标是;(3)、在坐标系中利用描点法画出此抛物线.
(1)、将y=x2-2x-3化成y=a(x-h)2+k的形式;(2)、与y轴的交点坐标是 , 与x轴的交点坐标是;(3)、在坐标系中利用描点法画出此抛物线.x
…
…
y
…
…
(4)、不等式x2-2x-3>0的解集是 .19. 如图,在Rt△ABC中,∠C=90°,D是AC边上一点,DE⊥AB于点E.若DE=2,BC=3,AC=6,求AE的长.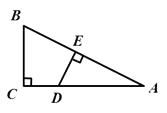 20. 若二次函数y=x2+bx+c的图象经过点(0,1)和(1,-2)两点,求此二次函数的表达式.21. 如图,在平面直角坐标系xOy中,反比例函数y= 的图象与一次函数y=-x+1的图象的一个交点为A(-1,m).
20. 若二次函数y=x2+bx+c的图象经过点(0,1)和(1,-2)两点,求此二次函数的表达式.21. 如图,在平面直角坐标系xOy中,反比例函数y= 的图象与一次函数y=-x+1的图象的一个交点为A(-1,m). (1)、求这个反比例函数的表达式;(2)、如果一次函数y=-x+1的图象与x轴交于点B(n,0),请确定当x<n时,对应的反比例函数y= 的值的范围.22. 如图,在▱ABCD中,点E在BC边上,点F在DC的延长线上,且∠DAE=∠F.
(1)、求这个反比例函数的表达式;(2)、如果一次函数y=-x+1的图象与x轴交于点B(n,0),请确定当x<n时,对应的反比例函数y= 的值的范围.22. 如图,在▱ABCD中,点E在BC边上,点F在DC的延长线上,且∠DAE=∠F.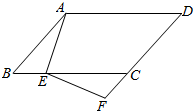 (1)、求证:△ABE∽△ECF;(2)、若AB=5,AD=8,BE=2,求FC的长.23. 如图,ABCD是一块边长为4米的正方形苗圃,园林部门拟将其改造为矩形AEFG的形状,其中点E在AB边上,点G在AD的延长线上,DG=2BE,设BE的长为x米,改造后苗圃AEFG的面积为y平方米.
(1)、求证:△ABE∽△ECF;(2)、若AB=5,AD=8,BE=2,求FC的长.23. 如图,ABCD是一块边长为4米的正方形苗圃,园林部门拟将其改造为矩形AEFG的形状,其中点E在AB边上,点G在AD的延长线上,DG=2BE,设BE的长为x米,改造后苗圃AEFG的面积为y平方米.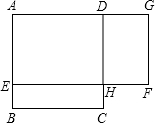 (1)、y与x之间的函数关系式为(不需写自变量的取值范围);(2)、根据改造方案,改造后的矩形苗圃AEFG的面积与原正方形苗圃ABCD的面积相等,请问此时BE的长为多少米?24. 已知抛物线y=x2-(2m-1)x+m2-m.(1)、求证:此抛物线与x轴必有两个不同的交点;(2)、若此抛物线与直线y=x-3m+3的一个交点在y轴上,求m的值.25. 如图,隧道的截面由抛物线ADC和矩形AOBC构成,矩形的长OB是12m,宽OA是4m.拱顶D到地面OB的距离是10m.若以O原点,OB所在的直线为x轴,OA所在的直线为y轴,建立直角坐标系.
(1)、y与x之间的函数关系式为(不需写自变量的取值范围);(2)、根据改造方案,改造后的矩形苗圃AEFG的面积与原正方形苗圃ABCD的面积相等,请问此时BE的长为多少米?24. 已知抛物线y=x2-(2m-1)x+m2-m.(1)、求证:此抛物线与x轴必有两个不同的交点;(2)、若此抛物线与直线y=x-3m+3的一个交点在y轴上,求m的值.25. 如图,隧道的截面由抛物线ADC和矩形AOBC构成,矩形的长OB是12m,宽OA是4m.拱顶D到地面OB的距离是10m.若以O原点,OB所在的直线为x轴,OA所在的直线为y轴,建立直角坐标系. (1)、画出直角坐标系xOy,并求出抛物线ADC的函数表达式;(2)、在抛物线型拱壁E、F处安装两盏灯,它们离地面OB的高度都是8m,则这两盏灯的水平距离EF是多少米?26. 有这样一个问题:探究函数y= (x-1)(x-2)(x-3)+x的性质.
(1)、画出直角坐标系xOy,并求出抛物线ADC的函数表达式;(2)、在抛物线型拱壁E、F处安装两盏灯,它们离地面OB的高度都是8m,则这两盏灯的水平距离EF是多少米?26. 有这样一个问题:探究函数y= (x-1)(x-2)(x-3)+x的性质. (1)、先从简单情况开始探究:
(1)、先从简单情况开始探究:①当函数y= (x-1)+x时,y随x增大而(填“增大”或“减小”);
②当函数y= (x-1)(x-2)+x时,它的图象与直线y=x的交点坐标为;
(2)、当函数y= (x-1)(x-2)(x-3)+x时,下表为其y与x的几组对应值.x
…
-
0
1
2
3
4
…
y
…
-
-3
1
2
3
7
…
①如图,在平面直角坐标系xOy中,描出了上表中各对对应值为坐标的点,请根据描出的点,画出该函数的图象;
②根据画出的函数图象,写出该函数的一条性质: ▲ 。
27. 如图,在平面直角坐标系中,抛物线y=x2+mx+n与x轴正半轴交于A,B两点(点A在点B左侧),与y轴交于点C.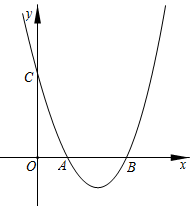 (1)、利用直尺和圆规,作出抛物线y=x2+mx+n的对称轴(尺规作图,保留作图痕迹,不写作法);(2)、若△OBC是等腰直角三角形,且其腰长为3,求抛物线的解析式;(3)、在(2)的条件下,点P为抛物线对称轴上的一点,则PA+PC的最小值为 .28. 已知四边形ABCD中,E,F分别是AB,AD边上的点,DE与CF交于点G.
(1)、利用直尺和圆规,作出抛物线y=x2+mx+n的对称轴(尺规作图,保留作图痕迹,不写作法);(2)、若△OBC是等腰直角三角形,且其腰长为3,求抛物线的解析式;(3)、在(2)的条件下,点P为抛物线对称轴上的一点,则PA+PC的最小值为 .28. 已知四边形ABCD中,E,F分别是AB,AD边上的点,DE与CF交于点G. (1)、如图1,若四边形ABCD是矩形,且DE⊥CF.则DE•CDCF•AD(填“<”或“=”或“>”);(2)、如图2,若四边形ABCD是平行四边形,试探究:当∠B与∠EGC满足什么关系时,使得DE•CD=CF•AD成立?并证明你的结论;(3)、如图3,若BA=BC=3,DA=DC=4,∠BAD=90°,DE⊥CF.则 的值为 .
(1)、如图1,若四边形ABCD是矩形,且DE⊥CF.则DE•CDCF•AD(填“<”或“=”或“>”);(2)、如图2,若四边形ABCD是平行四边形,试探究:当∠B与∠EGC满足什么关系时,使得DE•CD=CF•AD成立?并证明你的结论;(3)、如图3,若BA=BC=3,DA=DC=4,∠BAD=90°,DE⊥CF.则 的值为 .
-