2018-2019学年初中数学北师大版八年级下册1.2 直角三角形 同步练习
试卷更新日期：2019-01-14 类型：同步测试
一、单选题
-
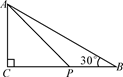
1. 下列命题的逆命题正确的是（ ）A、全等三角形的面积相等 B、全等三角形的周长相等 C、等腰三角形的两个底角相等 D、直角都相等2. 已知直角三角形ABC，有一个锐角等于50°，则另一个锐角的度数是（ ）.A、30° B、 40° C、45° D、50°3. 如图，△ABC中，∠C＝90°，AC＝3，∠B＝30°，点P是BC边上的动点，则AP长不可能是（ ）
A、3.5 B、4.2 C、5.8 D、74. 在下列条件：①∠A+∠B=∠C，②∠A∶∠B∶∠C=3∶4∶5，③∠C=∠A－∠B， ④a∶b∶c=3∶4∶5 中，能确定△ABC是直角三角形的条件有（ ）A、1个 B、2个 C、3个 D、4个5. 下列命题中，逆命题不正确的是（ ）A、两直线平行，同旁内角互补 B、直角三角形的两个锐角互余 C、全等三角形对应角相等 D、直角三角形斜边上的中线等于斜边的一半6. 如图是一个6×6的正方形网格，每个小正方形的顶点都是格点，Rt△ABC的顶点都在图中的格点上，其中点A、点B的位置如图所示，则点C可能的位置共有（ ）
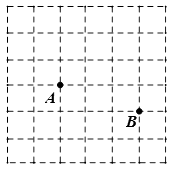A、9个 B、8个 C、7个 D、6个7. 如图，在Rt△ABC和Rt△A′B′C′中，∠C＝∠C′＝90°，那么在下列各条件中，不能判定Rt△ABC≌Rt△A′B′C′的是（ ）
A、AB＝A′B′＝5，BC＝B′C′＝3 B、AB＝B′C′＝5，∠A＝∠B′＝40° C、AC＝A′C′＝5，BC＝B′C′＝3 D、AC＝A′C′＝5，∠A＝∠A′＝40°8. 如图，AD是Rt△ABC斜边BC上的高，将△ACD沿AD所在的直线折叠，点C恰好落在BC的中点E处，则∠B等于（ ）
A、25° B、30° C、45° D、60°9. 若△ABC三边长a，b，c满足 + |b-a-2| + (c-8)2=0，则△ABC是（ ）A、等腰三角形 B、等边三角形 C、直角三角形 D、等腰直角三角形10. 如图，已知在Rt△ABC中，∠ACB=90°，∠ABC=60°，BC=2cm，F是BC边上的中点.若动点E从A点出发以2cm/s的速度沿着A→B→A方向运动，设运动时间为t(s)(0≤t＜3)，连结EF.当△BEF是直角三角形时，t的值为（ ）.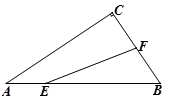
A、 B、1 C、 或1或 D、 或1或二、填空题
-
11. 命题“在同一个三角形中，等角对等边”的逆命题是 ．12. 若一个三角形三边长分别为 1.5，2，2.5，则这个三角形一定是三角形．
13. 如图，山坡的倾斜角∠ABC为30°，小明沿山坡BA从山脚B点步行到山顶A共走了100m，则山顶的高度AC是m．
14. 用直尺和圆规作△ABC，使BC=a，AC=b（a＞b），∠B=30°，若这样的三角形能作两个，则a，b间满足的关系式是 ．15. 如图，在△ABC中，∠ABC＝90°，∠A＝50°，CD＝CB，∠ABD＝ ．
16. 将一副三角尺如图所示叠放在一起，若 AB=4 cm，则阴影部分的面积是cm2
17. 在每个小正方形的边长为1的网格图形中，每个小正方形的顶点称为格点．以顶点都是格点的正方形ABCD的边为斜边，向内作四个全等的直角三角形，使四个直角顶点E，F，G，H都是格点，且四边形EFGH为正方形，我们把这样的图形称为格点弦图．例如，在如图1所示的格点弦图中，正方形ABCD的边长为 ，此时正方形EFGH的面积为5．问：当格点弦图中的正方形ABCD的边长为 时，正方形EFGH的面积的所有可能值是（不包括5）．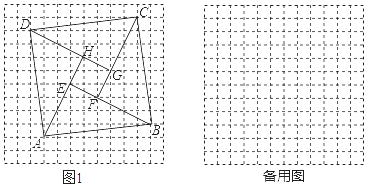
三、解答题
-
18. 如图，△ABC中，AB=AC，D点在BC上，∠1=30°，且∠4=60°，
求证：
(1)、AD=BD；(2)、CD=2BD．19. 如图，在△ABC中，∠BAC=∠ABC，点P在AB上，如果AD⊥CP，BE⊥CP的延长线，垂足分别为D，E，且BE=CD.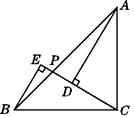
(1)、试探求这个图形中还有哪些相等的线段，并给出证明；(2)、试确定△ABC的形状.20. 如图，某中学有一块四边形的空地ABCD，学校计划在空地上种植草皮，经测量∠A=90°，AB=3m，BC=12m，CD=13m，DA=4m，若每平方米草皮需要200元，问学校需要投入多少资金买草皮？
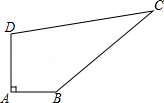21. 如图，对角线AB把四边形ACBE分为△ABC和△ABE两部分，如果△ABC中BC边上的高和△ABE中BE边上的高相等，且AC＝AE.
(1)、在原图上画出△ABC中BC边上的高AD与△ABE中BE边上的高AF；
(2)、请你猜想BC与BE的数量关系并证明．22. 如图所示，在△ACB中，∠ACB=90°，∠1=∠B．
(1)、求证：CD⊥AB；(2)、如果AC=8，BC=6，AB=10，求CD的长．23. 边长为6的等边△ABC中，点P从点A出发沿射线AB方向移动，同时点Q从点B出发，以相同的速度沿射线BC方向移动，连接AQ、CP，直线AQ、CP相交于点D．
(1)、如图①，当点P、Q分别在边AB、BC上时，①连接PQ，当△BPQ是直角三角形时，AP等于；
②∠CDQ的大小是否随P，Q的运动而变化？如果不会，请求出∠CDQ的度数；如果会，请说明理由；
(2)、当P、Q分别在边AB、BC的延长线上时，在图②中画出点D，并直接写出∠CDQ的度数．