2018-2019学年初中数学北师大版八年级下册1.1 等腰三角形 同步练习
试卷更新日期：2019-01-14 类型：同步测试
一、单选题
-
1. 对于命题“已知：a∥b，b∥c，求证：a∥c”．如果用反证法，应先假设（ ）
A、a不平行b B、b不平行c C、a⊥c D、a不平行c2. 应用反证法推出矛盾的推导过程中要把下列哪些作为条件使用（ ）①结论的否定；②已知条件；③公理、定理、定义等；④原结论．
A、①② B、②③ C、①②③ D、①②④3. 如图，在△ABC中，∠A＝36°，AB＝AC，BD是△ABC的角平分线．若在边AB上截取BE＝BC，连结DE，则图中等腰三角形共有（ ）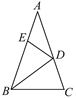
A、2个 B、3个 C、4个 D、5个4. 如图，在△ABC中，∠C=29°，D为边AC上一点，且AB=AD，DB=DC，则∠A的度数为（ ）
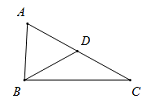A、54° B、58° C、61° D、64°5. 如图，上午8时，一艘船从A处出发以15海里/小时的速度向正北航行，10时到达B处，从A，B两点望灯塔C，测得∠NAC=42°，∠NBC=84°，则B处到灯塔C的距离为（ ）A、15海里 B、20海里 C、30海里 D、求不出来6. 如图，在△ABC中，AB=AC，∠B=50°，P为AB上的一个动点(不与顶点A重合)，则∠BPC的度数可能是（ ）
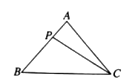A、135° B、85° C、50° D、40°7. 如图，在正方形ABCD的外侧，作等边三角形ADE，则∠AEB为（ ）
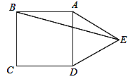A、10° B、15° C、20° D、125°8. 已知∠AOB=30°，点P在∠AOB内部，P1与P关于OB对称，P2与P关于OA对称，则P1 ， O，P2三点所构成的三角形是（ ）A、直角三角形 B、钝角三角形 C、等腰三角形 D、等边三角形9. 已知等腰三角形的一个内角是70°，则它的顶角的度数是（ ）A、70° B、40° C、70°或40° D、70°或30°10. △ABC中，①若AB＝BC＝CA，则△ABC是等边三角形；②属于轴对称图形，且有一个角为60°的三角形是等边三角形；③有三条对称轴的三角形是等边三角形；④有两个角是60°的三角形是等边三角形，上述结论中正确的有（ ）
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 等腰三角形的周长是18cm，其中一边长为4cm，其他两边分别长为12. 用反证法证明命题：“一个三角形中不能有两个直角”的过程归纳为以下三个步骤：
①∠A＋∠B＋∠C＝90°＋90°＋∠C>180°，这与三角形内角和为180°相矛盾，则∠A＝∠B＝90°不成立；②所以一个三角形中不能有两个直角；③假设∠A，∠B，∠C中有两个角是直角，不妨设∠A＝∠B＝90°.正确顺序的序号排列为
13. 如图，在Rt△ABC中，CD是斜边AB上的中线，若∠A=20°，则∠BDC= ．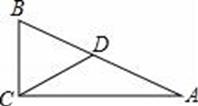
14. 在 中，AB=AC=13，BC=10，且 ⊥ 于点 ，则15. 如图，CD是Rt△ABC斜边AB上的高，将△ACD沿CD折叠，A点恰好落在AB的中点E处，则 B等于度.
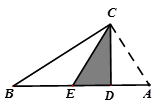16. 如图，过等边△ABC的顶点A作射线．若∠1＝20°，则∠2的度数为 ．
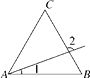17. 将数轴按如图所示从某一点开始折出一个等边三角形ABC，设点A表示的数为x﹣3，点B表示的数为2x+1，点C表示的数为﹣4，若将△ABC向右滚动，则x的值等于 ， 数字2012对应的点将与△ABC的顶点重合．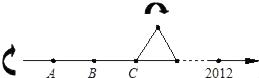
三、解答题
-
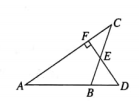
18. 如图，D为△ABC的边AB的延长线上一点，过D作DF⊥AC，垂足为F，交BC于E，且BD=BE.求证：△ABC是等腰三角形.
19. 如图，在△ABC中，AB=AC，∠BAC和∠ACB的平分线相交于点D，∠ADC=125°.求∠ACB和∠BAC的度数.
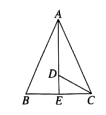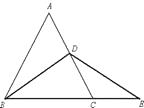
20. 已知：如图，在等边三角形ABC的AC边上取中点D，BC的延长线上取一点E，使BD=DE．求证：CD=CE.
21. 货轮在海上以每小时6海量的速度沿南偏东40°的方向航行，已知货轮在B处时，测得灯塔A在其北偏东80°的方向上，航行半小时后货轮到达C处，此时测得灯塔A在其北偏东20°的方向上，求货轮到达C处时与灯塔A的距离。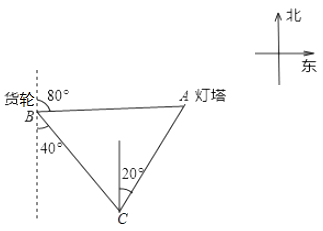
22. 如图，已知△ABC中，∠B=90 º，AB=8cm，BC=6cm，P、Q是△ABC边上的两个动点，其中点P从点A开始沿A→B方向运动，且速度为每秒1cm，点Q从点B开始沿B→C方向运动，且速度为每秒2cm，它们同时出发，设出发的时间为t秒．
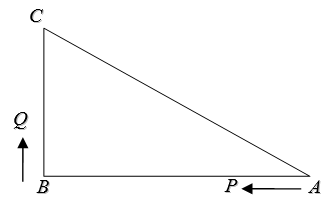(1)、当t=2秒时，求PQ的长；(2)、求出发时间为几秒时，△PQB是等腰三角形？(3)、若Q沿B→C→A方向运动，则当点Q在边CA上运动时，求能使△BCQ成为等腰三角形的运动时间．23. 如图， ABC是等边三角形，点D是线段AC上的一动点，E在BC的延长线上，且BD＝DE．(1)、如图，若点D为线段AC的中点，求证：AD＝CE；
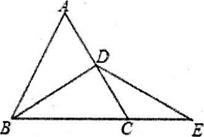(2)、如图，若点D为线段AC上任意一点，求证：AD＝CE.
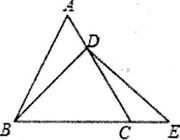24. 定义：如图1，等腰△ABC中，点E ， F分别在腰AB ， AC上，连结EF ， 若AE＝CF ， 则称EF为该等腰三角形的逆等线．
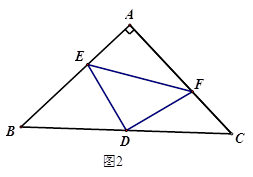
(1)、如图1，EF是等腰△ABC的逆等线，若EF⊥AB ， AB＝AC＝5，AE ＝2，求逆等线EF的长；(2)、如图2，若等腰直角△DEF的直角顶点D恰好为等腰直角△ABC底边BC上的中点，且点E ， F分别在AB ， AC上，求证：EF为等腰△ABC的逆等线；(3)、如图3，边长为6的等边三角形△AOC的边OC与X轴重合，EF是该等边三角形的逆等线．F点的坐标为（5， ）；试求点E的坐标(若需要，本题可以直接应用结论：在直角三角形中，30°角所对的直角边等于斜边的一半．)