重庆市南川三校联考2018-2019学年高二上学期理数期中考试试卷
试卷更新日期:2019-01-14 类型:期中考试
一、单选题
-
1. 已知直线的方程为 ,则该直线的倾斜角为A、
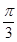 B、
B、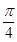 C、
C、 D、
D、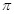 2. 已知点 点 ,则 为A、4 B、2 C、
2. 已知点 点 ,则 为A、4 B、2 C、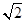 D、
3. 直线 与直线 的位置关系是A、平行 B、垂直 C、重合 D、相交但不垂直4. 如图,甲、乙、丙所示是三个立体图形的三视图,与甲乙丙相对应的标号是
D、
3. 直线 与直线 的位置关系是A、平行 B、垂直 C、重合 D、相交但不垂直4. 如图,甲、乙、丙所示是三个立体图形的三视图,与甲乙丙相对应的标号是长方体 圆锥 三棱锥 圆柱
 A、
A、 B、
B、 C、
C、 D、
D、 5. 已知球的表面积为 ,则该球的体积为A、
5. 已知球的表面积为 ,则该球的体积为A、 B、
B、 C、
C、 D、
D、 6. 若点 在以坐标原点为圆心的圆上,则该圆在点P处的切线方程为A、
6. 若点 在以坐标原点为圆心的圆上,则该圆在点P处的切线方程为A、 B、
B、 C、
C、 D、x=2
7. 已知圆 : ,圆 : ,则圆 与圆 的位置关系是A、相离 B、相交 C、外切 D、内切8. 设m,n表示不同的直线, , 表示不同的平面,给出下列命题
D、x=2
7. 已知圆 : ,圆 : ,则圆 与圆 的位置关系是A、相离 B、相交 C、外切 D、内切8. 设m,n表示不同的直线, , 表示不同的平面,给出下列命题若 , ,则 ; 若 , , ,则 ; 若 , , ,则 其中错误命题的个数为
A、0 B、1 C、2 D、39. 已知点A是圆 : 上一点,点B在直线l: 上,则 的最小值为A、 B、 C、
C、 D、3
10. 若直线 与圆 有公共点,则k的取值范围是A、
D、3
10. 若直线 与圆 有公共点,则k的取值范围是A、 B、
B、 C、
C、 D、
D、 11. 如图,在长方形 中, ,E,F分别是 , 的中点 有下列结论:
11. 如图,在长方形 中, ,E,F分别是 , 的中点 有下列结论:; 平面 ; 与 所成角为 ; 平面 .其中不成立的是
 A、
A、 B、
B、 C、
C、 D、
D、 12. 已知S,A,B,C是球O表面上的点, 平面ABC, , , ,则球O的体积等于A、
12. 已知S,A,B,C是球O表面上的点, 平面ABC, , , ,则球O的体积等于A、 B、
B、 C、
C、 D、
D、
二、填空题
-
13. 直线 : 与直线 : 的交点坐标为 .14. 已知一个矩形的长为3,宽为 以该矩形长为3的边为旋转轴旋转一周得到一个封闭几何体,则该几何体的表面积为 .15. 已知直线 和直线 互相平行,则它们之间的距离是 .16. 已知一块正方形薄铁片的边长为8cm,以它的一个顶点为圆心,一边长为半径画弧,沿弧剪下一个扇形 如图 ,若用这块扇形铁片围成一个无底的圆锥,则这个无底的圆锥的容积为 .

三、解答题
-
17. 直线l经过点 , 求直线l的点斜式、斜截式、一般式方程.18. 如图,AB是圆O的直径,点C是圆O上的动点,过动点C的直线SC垂直于圆O所在的平面,D,E分别是SA,SC的中点.

证明:
(1)、 平面ABC(2)、平面 平面SBC19. 已知某曲线的方程C: .(1)、若此曲线是圆,求a的取值范围,并指出圆心和半径;(2)、若 ,且与直线l: 相交于M,N两点,求弦长 .

