2018-2019学年初中数学浙教版九年级下册 2.3 三角形的内切圆 同步练习
试卷更新日期:2019-01-12 类型:同步测试
一、单选题
-
1. 内心和外心重合的三角形是( )A、直角三角形 B、钝角三角形 C、等腰三角形 D、等边三角形2. 如图,⊙O是△ABC的内切圆,则点O是△ABC的( )
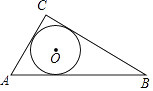 A、三条边的垂直平分线的交点 B、三条角平分线的交点 C、三条中线的交点 D、三条高的交点3. 下列说法正确的是( )A、三点确定一个圆 B、和半径垂直的直线是圆的切线 C、一个三角形只有一个外接圆 D、三角形的内心到三角形三个顶点的距离相等4. 如图,点I和O分别是△ABC的内心和外心,则∠AIB和∠AOB的关系为( )
A、三条边的垂直平分线的交点 B、三条角平分线的交点 C、三条中线的交点 D、三条高的交点3. 下列说法正确的是( )A、三点确定一个圆 B、和半径垂直的直线是圆的切线 C、一个三角形只有一个外接圆 D、三角形的内心到三角形三个顶点的距离相等4. 如图,点I和O分别是△ABC的内心和外心,则∠AIB和∠AOB的关系为( ) A、∠AIB=∠AOB B、∠AIB≠∠AOB C、4∠AIB-∠AOB=360° D、2∠AOB-∠AIB=180°5. 如图,在平面直角坐标系xOy中,A(4,0),B(0,3),C(4,3),I是△ABC的内心,将△ABC绕原点逆时针旋转90°后,I的对应点I'的坐标为( )
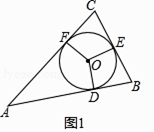
A、∠AIB=∠AOB B、∠AIB≠∠AOB C、4∠AIB-∠AOB=360° D、2∠AOB-∠AIB=180°5. 如图,在平面直角坐标系xOy中,A(4,0),B(0,3),C(4,3),I是△ABC的内心,将△ABC绕原点逆时针旋转90°后,I的对应点I'的坐标为( ) A、(﹣2,3) B、(﹣3,2) C、(3,﹣2) D、(2,﹣3)6. 如图,点I为△ABC的内心,AB=4,AC=3,BC=2,将∠ACB平移使其顶点与I重合,则图中阴影部分的周长为( )
A、(﹣2,3) B、(﹣3,2) C、(3,﹣2) D、(2,﹣3)6. 如图,点I为△ABC的内心,AB=4,AC=3,BC=2,将∠ACB平移使其顶点与I重合,则图中阴影部分的周长为( ) A、4.5 B、4 C、3 D、27. 若一直角三角形的斜边长为c,内切圆半径是r,则内切圆的面积与三角形面积之比是( )A、 B、 C、 D、8. 给出下列说法:
A、4.5 B、4 C、3 D、27. 若一直角三角形的斜边长为c,内切圆半径是r,则内切圆的面积与三角形面积之比是( )A、 B、 C、 D、8. 给出下列说法:①任意一个三角形一定有一个外接圆,并且只有一个外接圆;
②任意一个圆一定有一个内接三角形,并且只有一个内接三角形;
③任意一个三角形一定有一个内切圆,并且只有一个内切圆;
④任意一个圆一定有一个外切三角形,并且只有一个外切三角形.
其中正确的有 ( )
A、1个 B、2个 C、3个 D、4个9. 已知AC⊥BC于C,BC=a,CA=b,AB=c,下列选项中⊙O的半径为 的是( )A、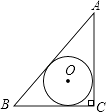 B、
B、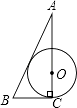 C、
C、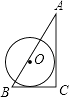 D、
D、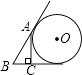 10. 如图,在直角边分别为3和4的直角三角形中,每多作一条斜边上的高就增加一个三角形的内切圆,以此类推,依此类推,图10中有10个直角三角形的内切圆,它们的面积分别记为S1 , S2 , S3 , …,S10 , 则S1+S2+S3+…+S10=( )
10. 如图,在直角边分别为3和4的直角三角形中,每多作一条斜边上的高就增加一个三角形的内切圆,以此类推,依此类推,图10中有10个直角三角形的内切圆,它们的面积分别记为S1 , S2 , S3 , …,S10 , 则S1+S2+S3+…+S10=( ) A、4π B、3π C、2π D、π
A、4π B、3π C、2π D、π二、填空题
-
11. 在△ABC中,∠C=90°,AB=10,且AC=6,则这个三角形的内切圆半径为 .12. 如图,△ABC是一块绿化带,将阴影部分修建为花圃,已知AB=13,AC=5,BC=12,阴影部分是△ABC的内切圆,这个圆的半径为 .
 13. 如图,已知△ABC的内切圆⊙O与BC边相切于点D,连结OB,OD.若∠ABC=40°,则∠BOD的度数是 .
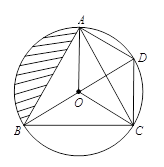
13. 如图,已知△ABC的内切圆⊙O与BC边相切于点D,连结OB,OD.若∠ABC=40°,则∠BOD的度数是 .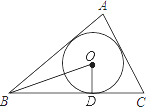 14. 如图,正六边形ABCDEF的边长是6+4 ,点O1 , O2分别是△ABF,△CDE的内心,则O1O2= .
14. 如图,正六边形ABCDEF的边长是6+4 ,点O1 , O2分别是△ABF,△CDE的内心,则O1O2= .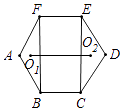 15. 在Rt△ABC中,∠C=90°,CA=8,CB=6,则△ABC内切圆的周长为16. 如图,在扇形CAB中,CD⊥AB,垂足为D,⊙E是△ACD的内切圆,连接AE,BE,则∠AEB的度数为 .
15. 在Rt△ABC中,∠C=90°,CA=8,CB=6,则△ABC内切圆的周长为16. 如图,在扇形CAB中,CD⊥AB,垂足为D,⊙E是△ACD的内切圆,连接AE,BE,则∠AEB的度数为 .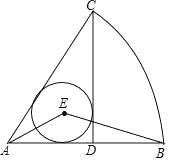
三、解答题
-
17.
如图,已知 , .
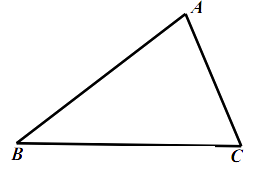 (1)、在图中,用尺规作出 的内切圆 ,并标出 与边 , , 的切点 , , (保留痕迹,不必写作法);(2)、连接 , ,求 的度数.18. 某新建小区要在一块等边三角形内修建一个圆形花坛.
(1)、在图中,用尺规作出 的内切圆 ,并标出 与边 , , 的切点 , , (保留痕迹,不必写作法);(2)、连接 , ,求 的度数.18. 某新建小区要在一块等边三角形内修建一个圆形花坛. (1)、要使花坛面积最大,请你用尺规画出圆形花坛示意图;(保留作图痕迹,不写做法)
(1)、要使花坛面积最大,请你用尺规画出圆形花坛示意图;(保留作图痕迹,不写做法)
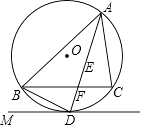
(2)、若这个等边三角形的周长为36米,请计算出花坛的面积.19. 如图,点E是△ABC的内心,AE的延长线交BC于点F,交△ABC的外接圆⊙O于点D,连接BD,过点D作直线DM,使∠BDM=∠DAC.(Ⅰ)求证:直线DM是⊙O的切线;
(Ⅱ)求证:DE2=DF•DA.