2018-2019学年初中数学浙教版九年级下册 2.1 直线和圆的位置关系 同步练习
试卷更新日期：2019-01-12 类型：同步测试
一、单选题
-
1. 如果一条直线与圆有公共点，那么该直线与圆的位置关系是（ ）A、相交 B、相离 C、相切 D、相交或相切2. 已知⊙O的半径为5cm，圆心O到直线l的距离为5cm，则直线l与⊙O的位置关系为（ ）
A、相交 B、相切 C、相离 D、无法确定3. 在平面直角坐标系中有点A(3，4)，以点A为圆心，5为半径画圆，在同一坐标系中直线y=－x与⊙A的位置关系是（ ）A、相离 B、相切 C、相交 D、以上都有可能4. 在平面直角坐标系中，经过点（4sin45°，2cos30°）的直线，与以原点为圆心，2为半径的圆的位置关系是（ ）A、相交 B、相切 C、相离 D、以上三者都有可能5. OA平分∠BOC，P是OA上任一点（O除外），若以P为圆心的⊙P与OC相离，那么⊙P与OB的位置关系是（ ）
A、相离 B、相切 C、相交 D、相交或相切6. 下列判断正确的是（ ）①直线上一点到圆心的距离大于半径，则直线与圆相离；②直线上一点到圆心的距离等于半径，则直线与圆相切；③直线上一点到圆心的距离小于半径，则直线与圆相交．
A、①②③ B、①② C、②③ D、③7. 如图，点D在⊙O的直径AB的延长线上，点C在⊙O上，且AC=CD，∠ACD=120°，CD是⊙O的切线：若⊙O的半径为2，则图中阴影部分的面积为（ ）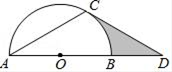
A、 2
﹣ 
π
B、 2 ﹣ 
π
C、
﹣ 
D、
﹣
8. 如图，☉O的圆心O到直线l的距离为3 cm，☉O的半径为1 cm，将直线l向右(垂直于l的方向)平移，使l与☉O相切，则平移的距离为（ ）
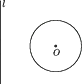A、1 cm B、2 cm C、4 cm D、2 cm或4 cm9. 如图，以点O为圆心的两个圆，半径分别为5和3，若大圆的弦AB与小圆相交，则弦AB的长度的取值范围是（ ）
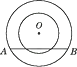A、8≤AB≤10 B、AB≥8 C、8<AB≤10 D、8<AB<1010. 已知☉O的半径r=3，设圆心O到一条直线的距离为d，圆上到这条直线的距离为2的点的个数为m，给出下列命题：①若d>5，则m=0；②若d=5，则m=1；③若1<d<5，则m=3；④若d=1，则m=2；⑤若d<1，则m=4.其中正确命题的个数是（ ）
A、1 B、3 C、4 D、511. 如图，在平面直角坐标系中，☉O的半径为1，则直线y=x- 与☉O的位置关系是（ ）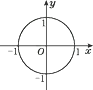
A、相离 B、相切 C、相交 D、以上三种情况都有可能12. 如图，直线AB、CD相交于点O，∠AOD=30°，半径为1cm的⊙P的圆心在射线OA上，且与点O的距离为6cm．如果⊙P以1cm/s的速度沿由A向B的方向移动，那么（ ）秒钟后⊙P与直线CD相切．
A、4 B、8 C、4或6 D、4或8二、填空题
-
13. 如图，正方形ABCD的边长为8，M是AB的中点，P是BC边上的动点，连结PM，以点P为圆心，PM长为半径作 当 与正方形ABCD的边相切时，BP的长为 ．
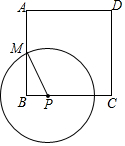14. 如图， PA、PB是⊙O的切线，切点为A、B，C是⊙O上一点(P与A、B不重合)，若∠P＝52°，则∠ACB=度.
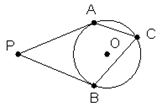15. 如图，⊙O与正五边形ABCDE的两边AE、CD分别相切于A、C两点，则∠AOC的度数为 ．
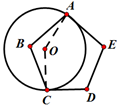16. 已知直线y=kx（k≠0）经过点（12，﹣5），将直线向上平移m（m＞0）个单位，若平移后得到的直线与半径为6的⊙O相交（点O为坐标原点），则m的取值范围为 ．17. 如图所示，在△ABC中，BC=4，以点A为圆心，2为半径的⊙A与BC相切于点D，交AB于点E，交AC于点F，且∠EAF=80°，则图中阴影部分的面积是 ．
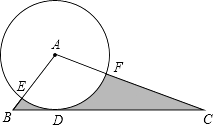18. 如图，AB是⊙O的直径，点D在AB的延长线上，DC切⊙O于点C，若∠A=24°，则∠D=°．
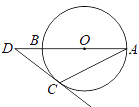19. 如图，以O为圆心的两个同心圆中，大圆的弦AB与小圆相切于点C，若大圆半径为10cm，小圆半径为6cm，则弦AB的长为 cm．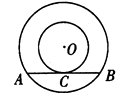
三、解答题
-
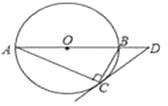
20. 如图，⊙O是Rt△ABC的外接圆，∠ACB=90°，∠A=25°，过点C作⊙O的切线，交AB的延长线于点D，求∠D的度数．
21. 如图，△ABC是直角三角形，∠ACB=90°，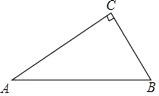
(1)、尺规作图：作⊙C，使它与AB相切于点D，与AC交于点E（保留作图痕迹，不写作法，请标明字母）；(2)、在你按（1）中要求所作的图中，若BC=3，∠A=30°，CD的长是22. 如图，在 Rt△ABC中，∠BAC=90°．
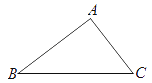(1)、先作∠ACB的平分线交AB边于点P，再以点P为圆心，PA长为半径作⊙P．（要求：尺规作图，保留作图痕迹，不写作法）
(2)、请你判断（1）中BC与⊙P的位置关系，并证明你的结论．
(3)、若AB=4，AC=3，求出（1）中⊙P的半径．
图① 
图②