2018-2019学年初中数学浙教版九年级下册 1.3 解直角三角形 同步练习
试卷更新日期：2019-01-12 类型：同步测试
一、单选题
-
1. 某人沿着坡度为1：2.4的斜坡向上前进了130m，那么他的高度上升了（ ）A、50m B、100m C、120m D、130m2. 如图，电线杆CD的高度为h，两根拉线AC与BC互相垂直（A，D，B在同一条直线上），设∠CAB=α，那么拉线BC的长度为（ ）
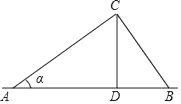A、 B、 C、 D、3. 如图，已知一商场自动扶梯的长l为13米，高度h为5米，自动扶梯与地面所成的夹角为θ，则tanθ的值等于（ ）
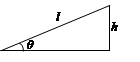A、 B、 C、 D、4. 在Rt△ABC中，∠C=90°，∠A=α，AC=3，则AB的长可以表示为（ ）A、 B、 C、3sinα D、3cosα5. 已知在Rt△ABC中，∠C=90°，AB=7，BC=5，那么下列式子中正确的是（ ）A、 B、 C、 D、6. 在Rt△ABC中，∠C=90°，sinA= ，则cosB的值为（ ）A、 B、 C、 D、7. 为测量被池塘相隔的两棵树 ， 的距离，数学课外兴趣小组的同学们设计了如图所示的测量方案：从树 沿着垂直于 的方向走到 ，再从 沿着垂直于 的方向走到 ， 为 上一点。其中 位同学分别测得三组数据：（1） ， ；（2） ， ， ；（3） ， ， 。其中能根据所测数据求得 ， 两树距离的有（ ）
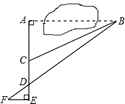A、0组 B、一组 C、二组 D、三组8. 如图，在四边形ABCD中，BD平分∠ABC，∠BAD=∠BDC=90°，E为BC的中点，AE与BD相交于点F．若BC=4，∠CBD=30°，则DF的长为（ ）
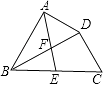A、 B、 C、 D、9. 如图，把边长为a cm的等边△ABC剪成四部分，从三角形三个顶点往下b cm处，呈 30°角 下剪刀，使中间部分形成一个小的等边△DEF.若△DEF的面积是△ABC的 ，则 的值为（ ）
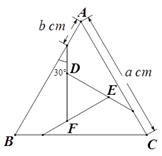A、 B、 C、 D、10. 小明在某次投篮中刚好把球打到篮板的点D处后进球．已知小明与篮框底的距离BC=5米，眼睛与地面的距离AB= 米，视线AD与水平线的夹角为∠α，已知tanα= ， 则点D到地面的距离CD是（ ）
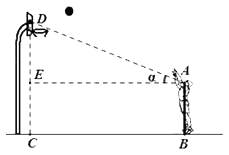A、2.7米 B、3.0米 C、3.2米 D、3.4米二、填空题
-
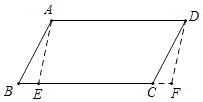
11. 如图，在▱ABCD中，AD=7，AB=2 ，∠B=60°．E是边BC上任意一点，沿AE剪开，将△ABE沿BC方向平移到△DCF的位置，得到四边形AEFD，则四边形AEFD周长的最小值为 ．
12. 如图，从甲楼底部A处测得乙楼顶部C处的仰角是30°，从甲楼顶部B处测得乙楼底部D处的俯角是45°，已知甲楼的高AB是120m，则乙楼的高CD是m（结果保留根号）
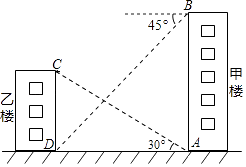13. 如图，某高速公路建设中需要测量某条江的宽度AB，飞机上的测量人员在C处测得A，B两点的俯角分别为45°和30°．若飞机离地面的高度CH为1200米，且点H，A，B在同一水平直线上，则这条江的宽度AB为米（结果保留根号）．
14. 如图，把三角形纸片折叠，使点 、点 都与点 重合，折痕分别为 ， ，得到 ，若 厘米，则 的边 的长为厘米.
15. 如图，某景区的两个景点A、B处于同一水平地面上、一架无人机在空中沿MN方向水平飞行进行航拍作业，MN与AB在同一铅直平面内，当无人机飞行至C处时、测得景点A的俯角为45°，景点B的俯角为知30°，此时C到地面的距离CD为100米，则两景点A、B间的距离为米（结果保留根号）．
16. 我国海域辽阔，渔业资源丰富．如图，现有渔船B在海岛A，C附近捕鱼作业，已知海岛C位于海岛A的北偏东45°方向上．在渔船B上测得海岛A位于渔船B的北偏西30°的方向上，此时海岛C恰好位于渔船B的正北方向18（1+ ）n mile处，则海岛A，C之间的距离为n mile．
三、解答题
-
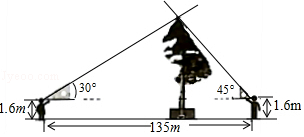
17. 清明节假期，小红和小阳随爸妈去旅游，他们在景点看到一棵古松树，小红惊讶的说：“呀！这棵树真高！有60多米．”小阳却不以为然：“60多米？我看没有．”两个人争论不休，爸爸笑着说：“别争了，正好我带了一副三角板，用你们学过的知识量一量、算一算，看谁说的对吧！”
小红和小阳进行了以下测量：如图所示，小红和小阳分别在树的东西两侧同一地平线上，他们用手平托三角板，保持三角板的一条直角边与地平面平行，然后前后移动各自位置，使目光沿着三角板的斜边正好经过树的最高点，这时，测得小红和小阳之间的距离为135米，他们的眼睛到地面的距离都是1.6米．通过计算说明小红和小阳谁的说法正确（计算结果精确到0.1）（参考数据 ≈1.41， ≈1.73， ≈2.24）
18. 某地发生8.1级地震，震源深度20千米．救援队火速赶往灾区救援，探测出某建筑物废墟下方点C处有生命迹象．在废墟一侧某面上选两探测点A、B，AB相距2米，探测线与该面的夹角分别是30°和45°（如图）．试确定生命所在点C与探测面的距离．（参考数据 ≈1.41， ≈1.73）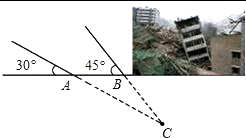
19. 如图，A，B两座城市相距100千米，现计划要在两座城市之间修筑一条高等级公路（即线段AB）。经测量，森林保护区中心P点在A城市的北偏东30°方向，B城市的北偏西45°方向上。已知森林保护区的范围在以P为圆心，50千米为半径的圆形区域内，请问：计划修筑的这条高等级公路会不会穿越保护区？为什么？
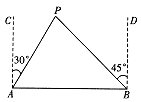20. 日照间距系数反映了房屋日照情况，如图①，当前后房屋都朝向正南时，日照间距系数 ，其中 为楼间水平距离， 为南侧楼房高度， 为北侧楼房底层窗台至地面高度.如图②，山坡 朝北， 长为 ，坡度为 ，山坡顶部平地 上有一高为 的楼房 ，底部 到 点的距离为 .
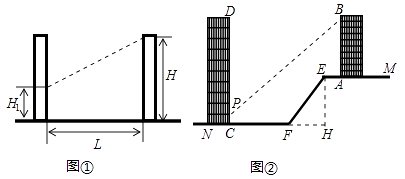(1)、求山坡 的水平宽度 ；(2)、欲在 楼正北侧山脚的平地 上建一楼房 ，已知该楼底层窗台 处至地面 处的高度为 ，要使该楼的日照间距系数不低于 ，底部 距 处至少多远？
21. 下图为某区域部分交通线路图，其中直线 ，直线 与直线 都垂直，垂足分别为点A、点B和点C，（高速路右侧边缘）， 上的点M位于点A的北偏东30°方向上，且BM＝ 千米， 上的点N位于点M的北偏东 方向上，且 ，MN= 千米，点A和点N是城际线L上的两个相邻的站点.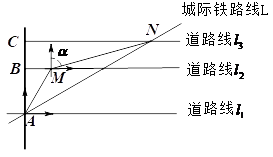
(1)、求 之间的距离(2)、若城际火车平均时速为150千米/小时，求市民小强乘坐城际火车从站点A到站点N需要多少小时？（结果用分数表示）22. 如图是小红在一次放风筝活动中某时段的示意图，她在A处时的风筝线（整个过程中风筝线近似地看作直线）与水平线构成30°角，线段AA1表示小红身高1.5米．
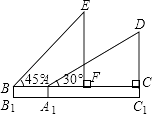(1)、当风筝的水平距离AC=18米时，求此时风筝线AD的长度；
(2)、当她从点A跑动9 米到达点B处时，风筝线与水平线构成45°角，此时风筝到达点E处，风筝的水平移动距离CF=10 米，这一过程中风筝线的长度保持不变，求风筝原来的高度C1D．