2016-2017学年重庆市重点中学八年级上学期期中数学试卷（b卷）
试卷更新日期：2017-04-11 类型：期中考试
一、选择题
-
1. 我国四个直辖市的地铁标识中是轴对称图形的是（ ）A、
B、
C、
D、
2.小明不慎将一块三角形的玻璃摔碎成如图所示的四块（即图中标有1、2、3、4的四块），你认为将其中的哪一些块带去，就能配一块与原来一样大小的三角形？应该带（ ）
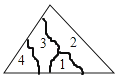A、第1块 B、第2块 C、第3块 D、第4块3. 如图，已知D、E在△ABC的边上，DE∥BC，∠B=60°，∠AED=40°，则∠A的度数为（ ）
A、100° B、90° C、80° D、70°4. 如图，已知点A，D，C，F在同一条直线上，AB=DE，BC=EF，要使△ABC≌△DEF，还需要添加一个条件是（ ）
A、∠BCA=∠F B、∠B=∠E C、BC∥EF D、∠A=∠EDF5. 若等腰三角形的一边长是2，另一边长是4，则它的周长为（ ）A、8 B、10 C、8或10 D、不能确定6. 如图，已知△ABC和△A′B′C′关于MN对称，并且AC=5，BC=2，A′B′=4，则△A′B′C′的周长是（ ）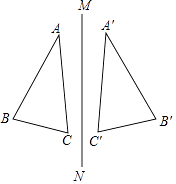
A、9 B、10 C、11 D、127. 如图，在△ABC中，AB=AC，AD=BD=BC，则∠A等于（ ）
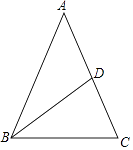A、16° B、36° C、48° D、60°8. 如图所示，AB=AC，AD=AE，∠BAC=∠DAE，∠1=25°，∠2=30°，则∠3=（ ）
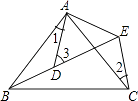A、55° B、50° C、45° D、60°9. 已知点P（﹣2，1）关于y轴的对称点为Q（m，n），则m﹣n的值是（ ）A、1 B、﹣1 C、3 D、﹣310. 如图，在△ABC中，∠ABC=∠C，AB=8，AB的垂直平分线DE交AB于点D，交AC于点E，△BEC的周长为13，则BC=（ ）
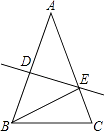A、5 B、6 C、7 D、811. 如图，将第一个图（图①）所示的正三角形连结各边中点进行分割，得到第二个图（图②）；再将第二个图中最中间的小正三角形按同样的方式进行分割，得到第三个图（图③）；再将第三个图中最中间的小正三角形按同样的方式进行分割，…，则得到的第五个图中，共有 个正三角形．（ ）
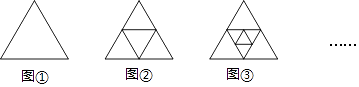A、14 B、15 C、16 D、1712. 如图，在△ABC中，AB=7，BC边上的中线AD的长为5，则AC的长可能是（ ）
A、3 B、10 C、17 D、20二、填空题
-
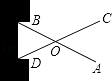
13. 如图，将两根钢条AB、CD的中点O连在一起，使AB、CD可以绕点O自由转动，就做成一个测量工件，则AC的长等于内槽宽BD，则△OBD≌△OAC的判定方法是（用字母表示）
14. 若一个多边形每个内角的度数都为150°，则这个多边形的边数为 ．15. 如图，在△ABC中，AB=AC，∠A=40°，AB的垂直平分线交AC于点E，垂足为点D，连接BE，则∠EBC的度数为°．
16. 等腰三角形的一个外角是100°，则这个等腰三角形的底角为 ．17. 如图，∠AOP=∠OPC=15°，PC∥DO，PD⊥OB，若OC=8，则PD等于 ．
18. 如图，直线l1∥l2∥l3 ， 且l1与l2的距离为1，l2与l3的距离为3．把一块含有45°角的直角三角板如图放置，顶点A、B、C恰好分别落在三条直线上，则△ABC的面积为 ．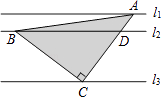
三、解答题
-
19. 如图，已知AB=AD，∠BAC=∠DAC，求证：△ABC≌△ADC．
20.如图，△ABC在平面直角坐标系中，点A、B、C的坐标分别为A（﹣2，1），B（﹣4，5），C（﹣5，2）．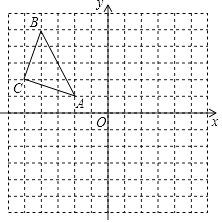
(1)、画出△ABC关于y对称的△A1B1C1 ， 其中，点A、B、C的对应点分别为A1、B1、C1；(2)、直接写出点A1、B1、C1的坐标； A1 ， B1 ， C1 ．(3)、△A1B1C1的面积是 ．四、解答题
-
21. 如图，AD是△ABC边BC上的高，BE平分∠ABC交AD于点E．若∠C=60°，∠BED=70°．求∠ABC和∠BAC的度数．
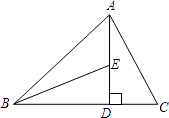22. 如图，已知点B，C，F，E在同一直线上，AB=DE，BC=EF，AB∥DE．求证：AC∥DF．
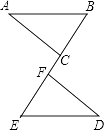23. 已知点A（2a﹣b，5+a），B（2b﹣1，﹣a+b）．(1)、若点A，B关于x轴对称，求a，b的值；(2)、若A，B关于y轴对称，求（4a+b）2016的值．24. 如图，△ABC是等边三角形，点E是AB的中点，延长CB至D，使BD= BC．
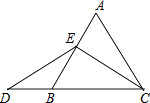(1)、用尺规作图的方法，过E点作EF⊥DC，垂足是点F；（不写作法，保留作图痕迹）(2)、求证：DF=CF．五、解答题
-
25. 如图，点C是线段AB上除点A、B外的任意一点，分别以AC、BC为边在线段AB的同旁作等边△ACD和等边△BCE，连接AE交DC于M，连接BD交CE于N，连接MN．
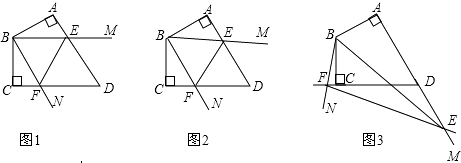
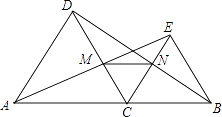(1)、求证：AE=BD；(2)、求证：MN∥AB．26. 已知四边形ABCD中，AB=BC，∠ABC=120°，∠MBN=60°，∠MBN绕B点旋转，它的两边分别交AD，DC（或它们的延长线）于E，F．当∠MBN绕B点旋转到AE=CF时（如图1），易证AE+CF=EF；
当∠MBN绕B点旋转到AE≠CF时，在图2和图3这两种情况下，上述结论是否成立？若成立，请给予证明；若不成立，线段AE，CF，EF又有怎样的数量关系？请写出你的猜想，不需证明．
