2016-2017学年山东省东营市垦利县八年级上学期期中数学试卷
试卷更新日期：2017-04-11 类型：期中考试
一、选择题
-
1. 下列图形中，是轴对称图形的是（ ）A、
B、
C、
D、
2. 如图，在平面直角坐标系xOy中，点P（﹣3，5）关于y轴的对称点的坐标为（ ）
A、（3，5） B、（﹣3，﹣5） C、（3，﹣5） D、（5，﹣3）3. 如图，OP为∠AOB的角平分线，PC⊥OA，PD⊥OB，垂足分别是C、D，则下列结论错误的是（ ）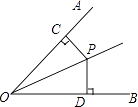
A、PC=PD B、∠CPD=∠DOP C、∠CPO=∠DPO D、OC=OD4. 如图，直线MN是四边形AMBN的对称轴，点P是直线MN上的点，下列判断错误的是（ ）
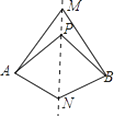A、AP=BN B、AM=BM C、∠MAP=∠MBP D、∠ANM=∠BNM5. 如图，过△ABC的顶点A，作BC边上的高，以下作法正确的是（ ）A、
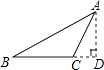B、
C、
D、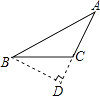
6. 如图，AE∥DF，AE=DF，要使△EAC≌△FDB，需要添加下列选项中的（ ）
A、∠A=∠D B、EC=BF C、AB=CD D、AB=BC7. 如图，AB∥CD，BP和CP分别平分∠ABC和∠DCB，AD过点P，且与AB垂直．若AD=8，则点P到BC的距离是（ ）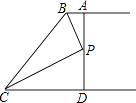
A、8 B、6 C、4 D、28. 两组邻边分别相等的四边形叫做“筝形”，如图，四边形ABCD是一个筝形，其中AD=CD，AB=CB，詹姆斯在探究筝形的性质时，得到如下结论：①AC⊥BD；②AO=CO= AC；③△ABD≌△CBD，
其中正确的结论有（ ）
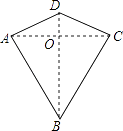A、0个 B、1个 C、2个 D、3个二、填空题
-
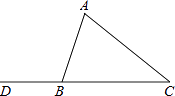
9. 正方形的对称轴有条．10. 一个正多边形的内角和为540°，则这个正多边形的每一个外角等于 ．11. 已知一个等腰三角形的两边长分别为2和4，则该等腰三角形的周长是 ．12. 如图，在△ABC中，∠C=40°，CA=CB，则△ABC的外角∠ABD=°．
13. 如图，∠3=30°，为了使白球反弹后能将黑球直接撞入袋中，那么击打白球时，必须保证∠1的度数为 ．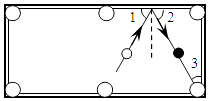
14. 如图，在Rt△ABC中，D，E为斜边AB上的两个点，且BD=BC，AE=AC，则∠DCE的大小为（度）．
15. 如图，在直角坐标系中，点A、B的坐标分别为（1，3）和（2，0），点C是y轴上的一个动点，且A、B、C三点不在同一条直线上，当△ABC的周长最小时，点C的坐标是 ．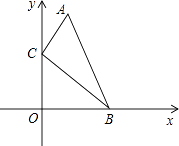
16. 在平面直角坐标系xOy中，已知点A（2，3），在坐标轴上找一点P，使得△AOP是等腰三角形，则这样的点P共有个．三、解答题
-
17. 如图，AC和BD相交于点O，OA=OC，OB=OD．求证：DC∥AB．
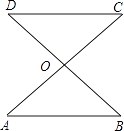18.在边长为1的小正方形网格中，△AOB的顶点均在格点上，
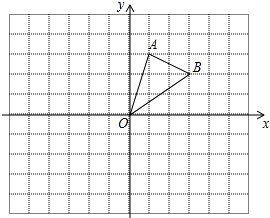(1)、B点关于y轴的对称点为；(2)、将△AOB向左平移3个单位长度得到△A1O1B1 ， 请画出△A1O1B1；(3)、画出△AOB关于x轴的对称图形△A2O2B2 ， 并写出点A2的坐标．
19.如图，已知AC⊥BC，BD⊥AD，AC与BD交于O，AC=BD．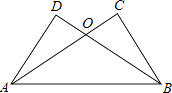
求证：
(1)、BC=AD(2)、△OAB是等腰三角形．20. 如图，在△ABC中，点D，E分别在边AC，AB上，BD与CE交于点O，给出下列三个条件：①∠EBO=∠DCO；②BE=CD；③OB=OC．
(1)、上述三个条件中，由哪两个条件可以判定△ABC是等腰三角形？（用序号写出所有成立的情形）(2)、请选择（1）中的一种情形，写出证明过程．21. 如图，将矩形ABCD沿BD对折，点A落在E处，BE与CD相交于F，若AD=3，BD=6．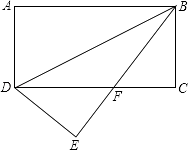
(1)、求证：△EDF≌△CBF；(2)、求∠EBC．22.【问题提出】
学习了三角形全等的判定方法（即“SAS”、“ASA”、“AAS”、“SSS”）和直角三角形全等的判定方法（即“HL”）后，我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究．
【初步思考】
我们不妨将问题用符号语言表示为：在△ABC和△DEF中，AC=DF，BC=EF，∠B=∠E，然后，对∠B进行分类，可分为“∠B是直角、钝角、锐角”三种情况进行探究．
【深入探究】
第一种情况：当∠B是直角时，△ABC≌△DEF．
(1)、如图①，在△ABC和△DEF，AC=DF，BC=EF，∠B=∠E=90°，根据 ， 可以知道Rt△ABC≌Rt△DEF．第二种情况：当∠B是钝角时，△ABC≌△DEF．
(2)、如图②，在△ABC和△DEF，AC=DF，BC=EF，∠B=∠E，且∠B、∠E都是钝角，求证：△ABC≌△DEF．第三种情况：当∠B是锐角时，△ABC和△DEF不一定全等．
(3)、在△ABC和△DEF，AC=DF，BC=EF，∠B=∠E，且∠B、∠E都是锐角，请你用尺规在图③中作出△DEF，使△DEF和△ABC不全等．（不写作法，保留作图痕迹）(4)、∠B还要满足什么条件，就可以使△ABC≌△DEF？请直接写出结论：在△ABC和△DEF中，AC=DF，BC=EF，∠B=∠E，且∠B、∠E都是锐角，若 ， 则△ABC≌△DEF．