2016-2017学年山东省滨州市八年级上学期期中数学试卷
试卷更新日期：2017-04-11 类型：期中考试
一、选择题
-
1. 下列几何图形不一定是轴对称图形的是（ ）A、线段 B、角 C、等腰三角形 D、直角三角形2. 等腰三角形的两边长分别是4cm和9cm，则它的周长是（ ）A、17cm B、22cm C、17cm或22cm D、无法确定3. 已知多边形的内角和是外角和的4倍，则这个多边形的边数为（ ）A、6 B、8 C、10 D、124. 如图，已知MB=ND，∠MBA=∠NDC，下列条件中不能判定△ABM≌△CDN的是（ ）
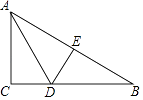
A、∠M=∠N B、AM=CN C、AB=CD D、AM∥CN5. 如图，△ABC中，∠C=90°，AC=BC，AD平分∠CAB交BC于D，DE⊥AB于E且AB=6cm，则△DEB的周长为（ ）cm．
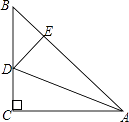A、6 B、8 C、10 D、126. 等腰三角形中，一个角为50°，则这个等腰三角形的顶角的度数为（ ）A、150° B、80° C、50°或80° D、70°7. 如图，在△ABC中，∠CAB=130°，AB、AC的垂直平分线分别交BC于点E、F则∠EAF等于（ ）
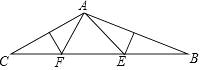A、60° B、70° C、80° D、90°8. 点M （﹣5，3）关于x轴的对称点的坐标是（ ）A、（﹣5，﹣3） B、（5，﹣3） C、（5，3） D、（﹣5，3）9. 根据下列已知条件，能唯一画出△ABC的是（ ）A、AB=3，BC=4，AC=8 B、AB=4，BC=3，∠A=30° C、∠A=60°，∠B=45°，AB=4 D、∠C=90°，AB=610. 将长方形纸片沿AC折叠后点B落在点E处，则线段BE与AC的关系是（ ）
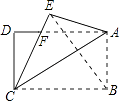A、AC=BE B、AC⊥BE C、AC⊥BE且AC=BE D、AC⊥BE且AC平分BE11. 如图为6个边长相等的正方形的组合图形，则∠1+∠2+∠3=（ ）
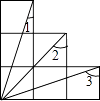A、90° B、135° C、150° D、180°12. 如图，OA、OB分别是线段MC、MD的垂直平分线，MD=5cm，MC=7cm，CD=10cm，一只小蚂蚁从点M出发爬到OA边上任意一点E，再爬到OB边上任意一点F，然后爬回M点处，则小蚂蚁爬行的路径最短可为（ ）
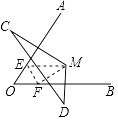A、12cm B、10cm C、7cm D、5cm二、填空题
-
13.
一个汽车车牌在水中的倒影为
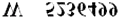，则该车的牌照号码是 ． 14. 如图，在△ABC中，∠ABC、∠ACB的平分线相交于F，过F作DE∥BC，交AB于D，交AC于E，那么下列结论：①△BDF、△CEF都是等腰三角形；②DE=DB+CE；③AD+DE+AE=AB+AC；④BF=CF．正确的有 ．
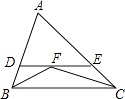15. 如图，∠A=50°，∠ABO=28°，∠ACO=32°，则∠BOC=度．
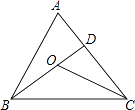16. 如图，AB=AC，∠A=40°，点D在AB的垂直平分线上，则∠DBC的度数是 ．
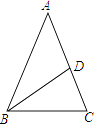17. 如图，正三角形ABC的周长为12cm，DC∥AB，AD⊥CD于D．则CD=cm．
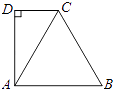18. 等腰三角形一腰上的高线与另一腰夹角为50°，则该三角形的顶角为 ．三、解答题
-
19. 作图题（保留作图痕迹，不写画法）．(1)、请在坐标系中，画出△ABC关于y轴对称的△A′B′C′．
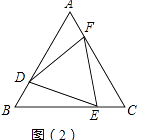
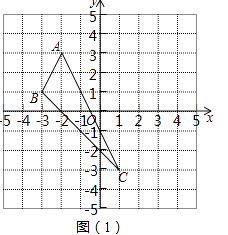(2)、如图（2），A与B是两个居住社区，OC与OD是两条交汇的公路，欲建立一个超市M，使它到A、B两个社区的距离相等，且到两条公路OC、OD的距离也相等．请利用尺规作图，确定超市M的位置．
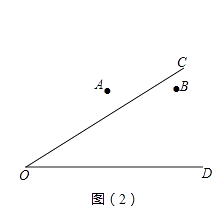20. 如图，在△ABC中，∠B=40°，∠C=62°，AD是△ABC的高，AE是△ABC的角平分线．求∠EAD的度数．
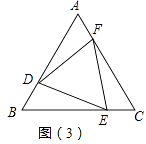
21. 如图，∠DCE=∠EBC=∠A=90°且DC=EC，猜测AB、AC、AD三者的数量关系，并说明理由．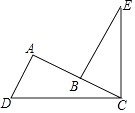
22. 如图，C是BE上一点，D是AC的中点，且AB=AC，DE=DB，∠A=60°，△ABC的周长是18cm．求∠E的度数及CE的长度．
