河南省南阳市淅川县2017-2018学年八年级上学期数学期中考试试卷

试卷更新日期：2019-01-11 类型：期中考试

进入出卷网下载

一、单选题

1. 在实数 $\sqrt{5}$ 、 $- 3$ 、0、 $\sqrt[3]{- 1}$ 、 $3.1415$ 、 $π$ 、 $\sqrt{144}$ 、 $\sqrt[3]{6}$ 、2.123122312223…… （1和3之间的2逐次加1个）中，无理数的个数为（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
2. 下面计算中，正确的是（）

A、 B、 C、 D、

查看试题解析
3. 若(x-3)(x+5)= $x^{2}$ +px+q，则p+q的值为（）

A、-15 B、2 C、17 D、-13

查看试题解析
4. 如图，△AOC≌△BOD，∠C与∠D是对应角，AC与BD是对应边，AD=10cm，OD=OC=2cm，那么OB的长是（）

A、8cm B、10cm C、2cm D、无祛确定

查看试题解析
5. 在△ABC中，AB=5，中线AD=6，则边AC的取值范围是（）

A、1<AC<11 B、5<AC<6 C、7<AC<17 D、11<AC<17

查看试题解析
6. 已知：如图，AC=CD，∠B=∠E=90°，AC⊥CD，则不正确的结论是（）

A、∠A与∠D互为余角 B、∠A=∠2 C、△ABC≌△CED D、∠1=∠2

查看试题解析
7. 把 $x^{4} y^{2} - x^{2} y^{4}$ 分解因式，其结果为（）

A、 ( )( ） B、 ( ) C、 D、 ( )

查看试题解析
8. 如图所示，在下列条件中，能判断△ARD $≌$ △BAC的条件是（）

①∠D=∠C，∠BAD=∠ABC；②∠BAD=∠ABC，AD=BC；③BD=AC，∠BAD=∠ABC；④AD=BC，BD=AC．

A、4个 B、3个 C、2个 D、1个

查看试题解析
9. 等腰三角形的周长为26cm，一边长为6cm，那么腰长为（　　）

A、6cm B、10cm C、6cm或10cm D、14cm

查看试题解析
10. 如图，AD是△ABC的中线，E，F分别是AD和AD延长线上的点，且DE=DF，连结BF，CE.下列说法：①△ABD和△ACD面积相等；②∠BAD=∠CAD；③△BDF≌△CDE；④BF∥CE；⑤CE=AE.其中正确的有（）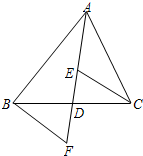

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 如果 $a^{m} = 3$ ， $a^{n} = 9$ ，则 $a^{3 m - 2 n} =$ .

查看试题解析
12. 等腰三角形的一个内角为50°，其他两个内角的度数为 .

查看试题解析
13. 长为a，宽为b的矩形，它的周长为16，面积为12，则 $a^{2} b + {ab}^{2}$ 的值为 .

查看试题解析
14.
如图，已知∠1=∠2=90°，AD=AE，那么图中有对全等三角形．

查看试题解析
15. 如图，将矩形纸片沿DE折叠后，点C落到T点C’处，已知∠DEC=35°，则∠ADC’= .

查看试题解析

三、解答题

16. 分解因式

(1)、 $- 4 x^{3} y + 4 x^{2} y^{2} - {xy}^{3}$

(2)、 $- 4 x^{3} y + 4 x^{2} y^{2} - {xy}^{3}$

(3)、 ${(x^{2} + 4)}^{2} - 16 x^{2}$

查看试题解析
17. 化简求值： $a (a - 2 b) + a (a + b) (a - b) + {(a + b)}^{2}$ ，其中 $a = - \frac{1}{2}$ ， $b = 1$ .

查看试题解析
18. 如图，点D在△ABC的AB边上，且∠ACD=∠A．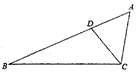

(1)、作∠BDC的平分线DE，交BC于点F（用尺规作图法，保留作图痕迹，不要求写作法）；

(2)、在(1)的条件下，判断直线DE与直线AC的位置关系，并说明理由.

查看试题解析
19. 对于任何实数，我们规定运算 $| \begin{matrix} a & b \\ c & d \end{matrix} | = ad - bc$ ，如： $| \begin{matrix} 1 & 2 \\ 3 & 4 \end{matrix} | = 1 \times 4 - 2 \times 3 = - 2$ .当 $x^{2} + 4 x + 4 = 0$ 时，求 $| \begin{matrix} 2 x + 3 & x + 2 \\ x - 2 & 2 x + 3 \end{matrix} |$ 的值.

查看试题解析
20. 如图，在△ABC和△DEF中，点B，E，C，F在同一直线上，请你再下列4个条件(①～④)中选3个条件作为题设，余下的1个作为结论，写出一个真命题，并证明.①AB=DE；②AC=DF；③∠ABC=∠DEF；④BE=CF.题设：．结论：．（填序号）

查看试题解析
21. 如图，在△ABC中，AB=AC，点D、E、F分别在AB、BC、AC上，且BD=CE，BE=CF．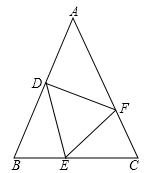

(1)、求证：△DEF是等腰三角形；

(2)、猜想：当∠A满足什么条件时，△DEF是等边三角形？并说明理由．

查看试题解析
22.

(1)、观察发现：四边形ABCD是正方形，点E是直线BC上的动点，连结AE，过点A作AF⊥AE交直线CD于F．当点E位于点B的左侧时，如图(1).观察线段AB．BE.CF之间有何数量关系？请直接写出线段AB．BE．CF之间的数量关系．

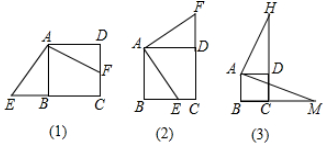(2)、拓展探究：当点E位于点B的右侧时，如图（2），线段AB．BE．CF之间有何数量关系？并说明理由.

(3)、迁移应用：如图（3），正方形ABCD的边长为2cm时，线段CM=3cm，直接写出线段CH的长.

查看试题解析
23. 如图，在等腰Rt△ABC中，∠C＝90°，D是斜边上AB上任一点，AE⊥CD于E ， BF⊥CD交CD的延长线于F ， CH⊥AB于H点，交AE于G ．

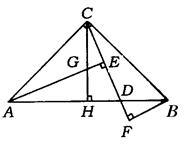(1)、试说明AH＝BH

(2)、求证：BD＝CG ．

(3)、探索AE与EF、BF之间的数量关系

查看试题解析