江西省赣州市五校协作体2018-2019学年高三上学期文数期中考试试卷
试卷更新日期:2019-01-11 类型:期中考试
一、单选题
-
1. 幂函数 的图像经过点 ,则 ( )A、1 B、
 C、
D、
C、
D、 2. 已知 , , ,则( )A、
2. 已知 , , ,则( )A、 B、
B、 C、
C、 D、
D、 3. 已知集合 ,且 ,则集合 的个数为( )A、 B、
3. 已知集合 ,且 ,则集合 的个数为( )A、 B、 C、
D、15
4. 函数 在 上的最大值与最小值的和为 ,则 ( )A、2 B、3 C、
C、
D、15
4. 函数 在 上的最大值与最小值的和为 ,则 ( )A、2 B、3 C、 D、
5. 下列函数中,在区间 上为增函数的是( )A、
D、
5. 下列函数中,在区间 上为增函数的是( )A、 B、
B、 C、
C、 D、
D、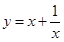 6. 下列说法正确的是( )A、函数
6. 下列说法正确的是( )A、函数 的图像关于
的图像关于  对称 .
B、将函数
对称 .
B、将函数  的图像上所有点的横坐标伸长到原来的
的图像上所有点的横坐标伸长到原来的  倍后得到
倍后得到  .
C、命题
.
C、命题  都是假命题,则命题“
都是假命题,则命题“  ”为真命题.
D、
”为真命题.
D、 ,函数
,函数  都不是偶函数.
7. 已知向量 与向量 平行,则锐角 等于( )A、
都不是偶函数.
7. 已知向量 与向量 平行,则锐角 等于( )A、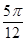 B、
B、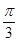 C、
C、 D、
D、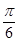 8. 已知奇函数 在 上单调递减,且 ,则不等式 的解集是( )A、
8. 已知奇函数 在 上单调递减,且 ,则不等式 的解集是( )A、 B、
B、 C、
C、 D、
D、 9. 已知函数 在 上有极值点,则 的取值范围是( )A、
9. 已知函数 在 上有极值点,则 的取值范围是( )A、 B、
B、 C、
C、 D、
D、 10. 在 中,点 为斜边 的中点, , , ,则 ( )A、
10. 在 中,点 为斜边 的中点, , , ,则 ( )A、 B、
B、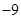 C、
C、 D、
D、 11. 已知函数 ,若方程 有三个不同的实数根,则实数 的取值范围是( )A、
11. 已知函数 ,若方程 有三个不同的实数根,则实数 的取值范围是( )A、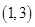 B、
C、
D、
B、
C、
D、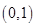 12. 定义在 函数 满足 , 且 时, ,则 ( )A、
12. 定义在 函数 满足 , 且 时, ,则 ( )A、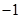 B、
C、1
D、
B、
C、1
D、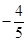
二、填空题
-
13. 命题“∃x∈R,x2+2x+2≤0”的否定是 .14. 已知单位向量 与 的夹角是 ,则 .15. 已知角 终边上有一点 ,则 .16. 在 中, ,则 的面积等于。
三、解答题
-
17. 已知集合 ,集合 .(1)、当 时,求 ;(2)、设 ,若“ ”是“ ”的必要不充分条件,求实数 的取值范围.18. 已知函数(1)、求函数 的最小正周期和单调增区间;(2)、当 时,求函数 的值域.19. 在 中, 分别为角 的对边, 已知(1)、求 值;(2)、若 ,且 的面积为 ,试求边长 的长.